Высота треугольника
Там, где есть высота, есть и прямой угол.
А значит, и прямоугольный треугольник, который поможет тебе решить массу задач!
И простые подобия, и «хитрые подобия с косинусом», и другие свойства прямоугольных треугольников!
И самое главное – не нужно ничего запоминать.
Научись выводить и никогда не ошибёшься, сможешь всегда себя проверить и решить любую задачу!
Все в этой статье. Читай и смотри видео.
Высота треугольника — коротко о главном
Высота – линия, проведённая из вершины треугольника перпендикулярно противоположной стороне (прямой, которая эту сторону содержит).
Основанием высоты называют ту точку, в которой высота пересекает противоположную сторону (или её продолжение).
Три высоты любого треугольника пересекаются в одной точке.
Высоты треугольника обратно пропорциональны сторонам, на которые они опущены: \( \displaystyle A{{H}_{A}}:B{{H}_{B}}:C{{H}_{C}}=\frac{1}{BC}:\frac{1}{AC}:\frac{1}{AB}\).
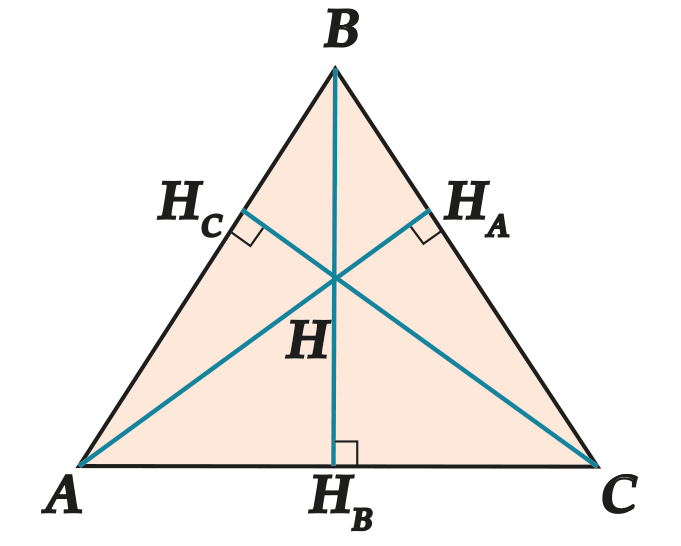
- Четыре способа вычисления длины высоты, проведенной к стороне BC:
Способ 1. Через сторону и угол треугольника: \( \displaystyle A{{H}_{A}}=AC\cdot \sin C=AB\cdot \sin B\).
Способ 2. Через все 3 стороны треугольника:\( \displaystyle A{{H}_{A}}=\frac{2}{BC}\cdot \sqrt{p\cdot (p-BC)\cdot (p-AC)\cdot (p-AB)}\), где \( \displaystyle p\) — полупериметр треугольника: \( \displaystyle p=\frac{AB+BC+AC}{2}\).
Способ 3. Через сторону и площадь треугольника: \( \displaystyle A{{H}_{A}}=\frac{2S}{BC}\).
Способ 4. Через стороны треугольника и радиус описанной окружности: \( \displaystyle A{{H}_{A}}=\frac{AB\cdot AC}{2R}\), где \( \displaystyle R\) — радиус описанной окружности.
Читай далее! Здесь не все…
Высота треугольника — подробнее
Высота – линия, проведённая из вершины треугольника перпендикулярно противоположной стороне (прямой, которая эту сторону содержит).
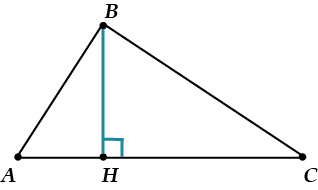
На этом рисунке \( \displaystyle BH\) – высота.
Но иногда высота (в отличие от биссектрисы и медианы) ведёт себя, как непослушный ребенок – «выбегает» из треугольника. Это бывает в тупоугольном треугольнике.
И тогда получается так:
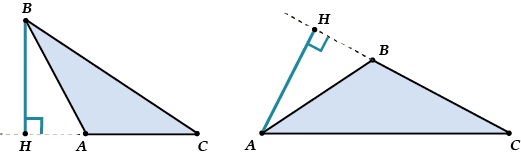
В общем, не нужно пугаться, если основание высоты оказалось не на стороне треугольника, а «за» треугольником, на продолжении стороны.
Как же решать задачи, в которых участвует высота?
Нужно стремиться применить какие-нибудь знания о прямоугольном треугольнике – ведь где высота – там и прямой угол.
Но попадаются задачи и похитрее, при решении которых лучше обладать дополнительными знаниями заранее, а не выводить их «с нуля». Сейчас мы обсудим некоторые из них.
Но для начала решим простенькую задачку на высоту в тупоугольном треугольнике:
В треугольнике \( \displaystyle ABC\) с тупым углом \( \displaystyle C\) проведена высота \( \displaystyle BH\). Найти \( \displaystyle AC\), если \( AB=2\sqrt{10}\), \( BC=\sqrt{13}\), \( BH=2\).
Смотри: из-за того, что угол \( C\) – тупой, высота \( BH\) опустилась на продолжение стороны \( AC\), а не на саму сторону.
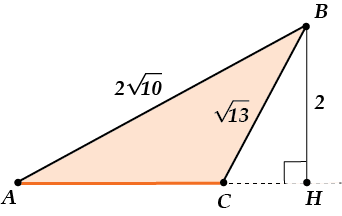
Теперь давай увидим во всём этом два прямоугольных треугольника.
Смотри их целых два:
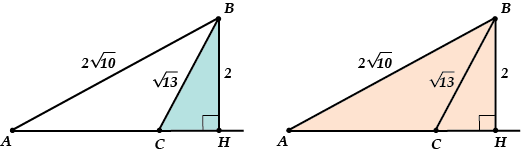
Применяем теорему Пифагора к треугольнику \( BCH\):
\( B{{C}^{2}}=B{{H}^{2}}+C{{H}^{2}}\), то есть \( 13=4+C{{H}^{2}}\); \( CH=3\).
А теперь теорема Пифагора для \( \Delta ABH\):
\( A{{B}^{2}}=A{{H}^{2}}+B{{H}^{2}}\); то есть \( 40=A{{H}^{2}}+4\); \( AH=6\).
Теперь осталось только заметить, что \( AC=AH-CH=6-3=3\).
Нашли!
А теперь давай вернемся к нашим высотам!
В треугольнике проведено две высоты
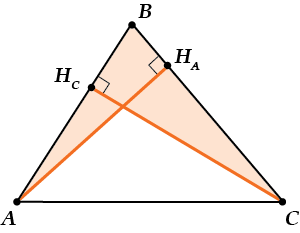
Первый «неожиданный факт»:
\( \displaystyle \Delta AB{{H}_{A}}\sim \Delta ~CB{{H}_{C}}\)
Почему бы это? Да очень просто! У них общий угол \( \displaystyle B\) и оба – прямоугольные. Значит, подобны по двум углам.
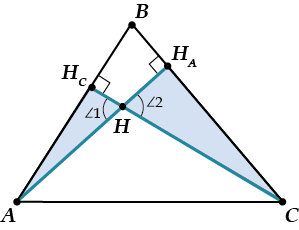
Второй «неожиданный» факт:
\( \Delta A{{H}_{C}}H\sim{\ }\Delta C{{H}_{A}}H\)
Здесь тоже подобие по двум углам: \( \angle 1=\angle 2\) (как вертикальные) и по прямому углу.
Третий, по-настоящему неожиданный факт:
\( \Delta ABC\sim \Delta {{H}_{A}}B{{H}_{C}}\)
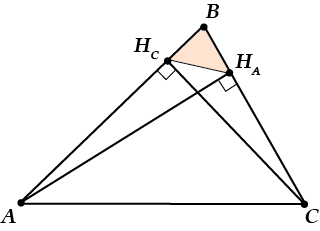
Вот это уже интереснее, правда? Давай разбираться, почему так.
В треугольнике проведены три высоты
Как и для медиан, и для биссектрис, для высот треугольника верно следующее утверждение:
В любом треугольнике три высоты или их продолжения пересекаются в одной точке.
Доказывать это утверждение мы здесь, пожалуй, не будем.
Давай просто нарисуем, чтобы понять, как это бывает «высоты или их продолжения».
1. Треугольник остроугольный – тогда пересекаются сами высоты:
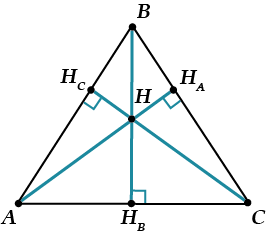
2. Треугольник тупоугольный – тогда пересекаются продолжения высот:
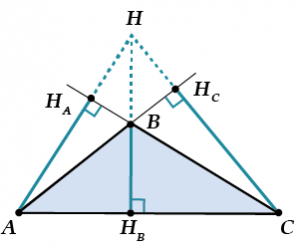
Что же полезного мы ещё не обсудили?
Угол между высотами
Давай узнаем, вдруг угол между высотами можно как–то выразить через углы треугольника? Давай рассмотрим остроугольный треугольник.
Итак, нам хотелось бы найти \( \displaystyle \angle \varphi \).
Смотрим на \( \displaystyle \Delta AHC\). Замечаем, что наш \( \displaystyle \angle \varphi \) – внешний угол в этом треугольнике.
Значит, \( \angle \varphi =\angle 1+\angle 2\).
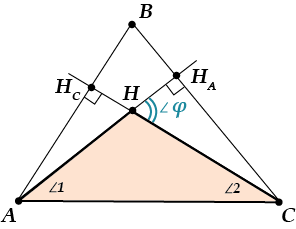
Чему же равны \( \displaystyle \angle 1\) и \( \displaystyle \angle 2\)?
Смотри: из \( \Delta A{{H}_{A}}C\) выходит, что \( \angle 1=90{}^\circ -\angle C\).
Конечно, таким же образом из \( \Delta C{{H}_{C}}A\) получается, что \( \angle 2=90{}^\circ -\angle A\).
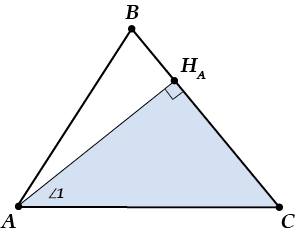
Теперь \( \angle ~\varphi =\angle ~1+\angle ~2=90{}^\circ -\angle ~C+90{}^\circ -\angle ~A=180{}^\circ -\angle ~A-\angle ~C\).
Но что же это такое? Ведь сумма угла углов треугольника — \( 180{}^\circ \)! Значит, \( \angle \varphi =\angle B\).
Итак, что получилось?
Остроугольный треугольник и высота
Вернёмся–ка к остроугольному треугольнику. Отметим на рисунке равные углы:
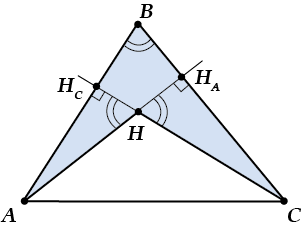
Что видим теперь? Ещё подобные треугольники!
Как от двух линий вообще могут получиться столько подобных треугольников?!
Но тем не менее…
\( \Delta C{{H}_{C}}B\sim \Delta C{{H}_{A}}H\sim \Delta A{{H}_{A}}B\sim \Delta A{{H}_{C}}H\)Видишь, какое богатство? И всё это может быть использовано в задачах!
Ну вот, теперь ты узнал что-то новенькое про высоты треугольника.
Теперь пробуй применять в задачах всё это – и соображение о том, что высота образует прямоугольный треугольник, и простые подобия прямоугольных треугольников, получающихся при пересечении двух высот, и подобие похитрее — которое с косинусом, и то, что угол между высотами равен углу между сторонами…
Главное, ты не старался просто запоминать все эти факты, а осознай, что их можно очень просто вывести.
И тогда, если ты будешь точно знать, например, что две проведённые высоты приносят кучу бонусов в виде всяких подобий, то ты непременно и сам получишь все эти бонусы, а заодно – решение своей задачи!
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №6 Все о равнобедренном треугольнике
Очень часто все «проблемы» с решением задач на равнобедренный треугольник решаются построением высоты!!!
Очень хороший вебинар, чтобы закрепить решением задач то, что вы изучили в этой статье о высоте.
Вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Научимся решать и «обычные» треугольники.
ЕГЭ №6 Все о прямоугольном треугольнике
Важнейшая тема — прямоугольный треугольник — свойства, теорема Пифагора, тригонометрия.
Абсолютное большинство задач геометрии сводятся к прямоугольным треугольникам. Поэтому знать нужно как «Отче наш».
И уметь решать задачи — чем мы займемся на этом вебинаре.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Дарья Сулейманова
15 января 2018
Сидела и готовилась к зачёту по геометрии около двух часов, заходила на множество разных сайтов. И только на вашем сайте всё написано понятным языком, без заумных терминов. Спасибо!
Александр (админ)
15 января 2018
Дарья, спасибо! Всей нашей команде очень приятно это слышать. Мы, консультанты, убеждали математиков использовать «человеческий» язык. И они справились очень хорошо. В результате получилось то, что всем нравится. Мы каждый день получаем благодарности. Еще раз спасибо и удачи на зачете!
Олеся
06 апреля 2018
Готовится с внуком к ОГЭ. Школу закончила 45 лет назад. Учили в то время просто отлично. Многое помню хорошо, но некоторые нюансы забылись. Ваш сайт очень помог. Все лаконично, по существу и без лишних заумных оборотов. Скачала ла себе на телефон. В свободное время просматриваю. С удовольствием решаю задачи. Спасибо Вам.
Александр (админ)
06 апреля 2018
Олеся, спасибо за такой отзыв и удачи Вашему внуку на всех экзаменах. А сайт я лично попросил математиков написать «человеческим языком» ) Судя по отзывам, они справились.
Ольга
15 февраля 2019
А как бы еще доказать подобие треугольников HcHHa и АНС Можно без окружностей
Дмитрий
10 февраля 2020
Скажите, прав ли я. (Задание «Угол между высотами») Что не может угол Фи быть = углу В Так как, угол В это 180 минус угол А+С И угол Н это 180 минус угол А+С Значит В и Н равны, следовательно угол Фи это 180 — Н или минус В, что априори не может быть равным не В не Н.
Алексей Шевчук
13 февраля 2020
Дмитрий, угол H — это угол в треугольнике AHC, но в этом треугольнике углы A и С не равны углам A и C треугольника ABC. Чтобы не возникало такой путаницы, важно (а на экзаменах даже обязательно) писать углы полностью (тремя вершинами): ∠AHC = 180 — (∠HAC + ∠HCA); ∠ABC = 180 — (∠BAC + ∠BCA) — и теперь сразу видно, что это не одно и то же.
Андрей
08 апреля 2020
Очень доходчивый язык учебника. Как в старой советской школе. Я просто в восторге
Александр (админ)
08 апреля 2020
Андрей, спасибо большое! Очень приятно слышать! Сравнение лестное! ))