Логарифмические неравенства на ЕГЭ
Ты что, еще не научился решать логарифмические неравенства?!
Да ладно?! Это же легко!
Шучу. На самом деле, логарифмические неравенства – сложная тема. И за нее дают много баллов на ЕГЭ.
Сейчас для тебя эта тема станет простой.
Я тебе ВСЁ объясню, и ты сможешь решить ЛЮБОЕ логарифмическое неравенство.
Поехали!
Логарифмические неравенства — коротко о главном
Определение логарифмического неравенства
Простейшим логарифмическим неравенством является соотношение вида:
\( \displaystyle lo{{g}_{a}}~f\left( x \right)~>~lo{{g}_{a}}g\left( x \right)\),
где \( \displaystyle f\left( x \right)\) и \( \displaystyle g\left( x \right)\) – некоторое выражение, зависящее от \( \displaystyle x\) (например, \( \displaystyle f\left( x \right)=1+2x+{{x}^{2}},~g\left( x \right)=3{x}-1).\)
знак \( \displaystyle >\) можно заменить на один из трех знаков: \( \displaystyle ~\ge ,~\le ,~<\).
- \( \displaystyle lo{{g}_{a}}~f\left( x \right)~>lo{{g}_{a}}~g\left( x \right)~=>~f\left( x \right)>g\left( x \right)\) при \( \displaystyle a>1\)
- \( \displaystyle lo{{g}_{a}}~f\left( x \right)~>lo{{g}_{a}}~g\left( x \right)~=>~f\left( x \right)<g\left( x \right)\) при \( \displaystyle 0<a<1\)
Алгоритм решения логарифмических неравенств
Алгоритм решения простейших логарифмических неравенств вида \( \displaystyle lo{{g}_{a}}~f\left( x \right)~>~lo{{g}_{a}}~g\left( x \right)~\):
- Находим ОДЗ: \( \left\{ \begin{array}{l}f\left( x \right)>0\\g\left( x \right)>0\end{array} \right.\) (я напомню, что знак системы (фигурная скобка) означает, что должны выполняться одновременно оба неравенства;
- Смотрим на основание: если \( a>1\), то решаем неравенство \( f\left( x \right)>g\left( x \right).\) Если же \( 0<a<1\), то решаем \( f\left( x \right)<g\left( x \right)\);
- Совмещаем полученное решение неравенства из пункта 2 с нашим ОДЗ из пункта 1.
«Логарифмические» и «неравенства». Оба слова тебе знакомы по отдельности?
Я очень надеюсь, что да. Иначе я настоятельно рекомендую (очень-очень прошу!) прочитать и освоить следующие разделы:
- Логарифмы
- Свойства степени
- Решение логарифмических уравнений
- Решение линейных неравенств
- Метод интервалов
Эти материалы очень важны для сдачи ЕГЭ по математике на максимум и поступления в ВУЗ мечты! Учти это!
Ну что, весь материал улегся в голове? Теперь ты легко сможешь ответить на вопрос, скажем, чему равен \( lo{{g}_{3}}81\), ведь ясно, что это \( 4\), правда?
А почему?
Да потому, что \( {{3}^{4}}=81\), а логарифм – это и есть та степень, в которую нужно возвести маленькое число снизу (в данном случае \( 3\)), чтобы получить большое число сверху (то есть \( 81\)).
А вот ты знаешь, чему в точности равно \( lo{{g}_{2}}3\)? Нет? И я нет, и никто не знает. (Для меня с такого постулата началась математика, что никто и ничего не знает)
А все почему?
Да потому что нет целой степени двойки такой, чтобы двойка в ней равнялась трем. Факт есть факт.
То есть логарифм, можно сказать, обобщает понятие степени.
Ну что я все про логарифмы да про логарифмы… Ты ведь мне пообещал, что прочитаешь все материалы по ним самостоятельно, и я тебе в этом вопросе полностью доверяю.
Как доверяю и в том, что с неравенствами (хотя бы простейшими), ты тоже на «ты». Ну если не совсем на «ты», то хотя бы не пугаешься одного их вида. Они же не кусаются. Тебе ведь совершенно очевидно, что неравенство, скажем
\( 4{x} -2<0\)
имеет решение \( x<\frac{1}{2}\), или, как мы это обычно записываем, \( x\in \left( -\infty ;0.5 \right).\)
Ты ведь грамотный читатель и тебе не надо лишний раз напоминать, что
При делении (или умножении) на положительное число знак неравенства не меняется, а при умножении на отрицательное – меняется на противоположный?
Еще раз очень прошу тебя, если мои слова тебе мало что говорят, то срочно, прямо сейчас перечитай методы решения простейших линейных неравенств.
Азов нам пока что хватит.
Ну все, теперь, я думаю, самое время переходить к внешнему виду логарифма. Давай посмотрим на него повнимательнее.
Как выглядит логарифм
\( lo{{g}_{a}}b\),
где \( a\) – основание, а \( b\) – подлогарифменное выражение.
А сам логарифм равен степени, в которую нужно возвести основание, чтобы получить подлогарифменное выражение. Хотя ты и так все это помнишь. Ты также прекрасно помнишь, что из определения логарифма следует:
\( a>0,~a\ne 1,~b>0~\)
Ну все, теперь наша с тобой цель это скрестить бульдога с носорогом, где бульдогом будет логарифмы, а носорогом – неравенства. Так что же мы получим? Как ты уже догадался, результатом этого эксперимента будут логарифмические неравенства.
Хорошенько запомни эти три соотношения, они помогут тебе избежать глупейших ошибок при решении примеров.
Что такое логарифмические неравенства
Простейшим логарифмическим неравенством является соотношение вида: \( lo{{g}_{a}}~f\left( x \right)~>~lo{{g}_{a}}g\left( x \right)\), где \( f\left( x \right)\) и \( g\left( x \right)\) – некоторое выражение, зависящее от \( x\) (например, \( f\left( x \right)=1+2x+{{x}^{2}},~g\left( x \right)=3{x} -1).\)
«И что?» — скажешь ты. – «Зачем мне нужно непонятное определение, если в нем не говорится, как с его помощью решать эти самые логарифмические неравенства».Конечно же, ты можешь сформулировать еще три определения простейшего логарифмического неравенства, просто заменив знак \( >\) на один из трех знаков: \( ~\ge ,~\le ,~<\).
Дай мне минутку и все встанет на свои места. Но прежде давай рассмотрим крошечный пример.
\( log{{~}_{2}}\left( 2x+4 \right)~>~log{{~}_{2}}3\)
Прежде всего, когда мы решаем логарифмическое неравенство, мы должны позаботиться о такой противной штуке, как область допустимых значений (ОДЗ).
ОДЗ логарифмического неравенства
Для логарифма (из его определения) следует, что \( 2x+4~>~0\) (сейчас \( 2x+4~\) выступает в роли \( b\) в определении логарифма).
А как мы помним, это число обязано быть положительным (еще раз посмотри на определение логарифмического неравенства), я предупреждал, что это очень важно.
Это неравенство ты без труда решишь и скажешь, что \( x\) обязан быть больше \( -2.\)
Ну вот, с ОДЗ мы разобрались, время переходить непосредственно к решению неравенства \( log{{~}_{2}}\left( 2x+4 \right)~>~log{{~}_{2}}3\).
Давайте просто отбросим \( lo{{g}_{2}}\) из левой и правой частей нашего неравенства. Тогда у нас останется \( 2x+4~>~3\), откуда \( 2x~>~-1\) и \( x~>~-\frac{1}{2}\). Теперь наша с тобой цель – это «совместить» полученное решение с ОДЗ.
\( \left\{ \begin{array}{l}x>~-2\\x>~-\frac{1}{2}\end{array} \right.\)
Отметим эти точки (ты догадался, что под точками я имею в виду \( -2\) и \( -\frac{1}{2}\)).
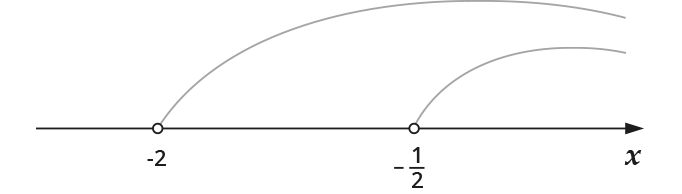
Теперь тебе ясно, что является решением нашего исходного неравенства? Да, ты абсолютно прав, это та область, где проходят две дужки. Тогда запишем ответ:
\( x\in \left( -0.5;+\infty \right).\)
А вот тебе тот же самый пример, но я изменю в нем лишь самую малость:
\( log_{0.2}~\left( 2x+4 \right)~>~log_{0.2}~3\)
Ты без труда заметил, что изменилось совсем немного – я лишь поменял основание с \( \displaystyle 2\) на \( \displaystyle 0.2.\)
Однако решение примера изменится от этого кардинально.
О нет, ОДЗ не изменится, куда уж ему деться. Тут все по-прежнему. ОДЗ: \( \displaystyle \text{x}>~-2\).
А вот само неравенство, которое равносильно исходному, преобразится: из \( \displaystyle lo{{g}_{0.2}}~\left( 2x+4 \right)>~lo{{g}_{0.2}}~3\) у нас теперь будет следовать, что \( \displaystyle 2x+4<3\).
Отчего же это произошло? Кто виноват?
А виновато основание, и только оно.
Ничего, как только мы решим до конца этот пример, я сформулирую соответствующее простое правило.
А пока что решим простейшее неравенство: \( \displaystyle 2x+4< 3 \Rightarrow x<-\frac{1}{2}\).
Тогда исходное неравенство равносильно вот такой системе:
\( \displaystyle \left\{ \begin{array}{l}x>~-2\\x<~-\frac{1}{2}\end{array} \right.\)И ее решением будет промежуток: \( \displaystyle x\in \left( -2;-\frac{1}{2} \right).\)
Все еще под впечатлением?
Изменилось ведь всего ничего (основание такое маленькое, что иногда и незаметно вовсе), а решение стало совсем другим.
Решение логарифмических неравенств
Теперь давай, наконец, запишем долгожданное правило.
\( \displaystyle lo{{g}_{a}}~f\left( x \right)~>lo{{g}_{a}}~g\left( x \right)~=>~f\left( x \right)>g\left( x \right)\) при \( \displaystyle a>1\) \( \displaystyle lo{{g}_{a}}f\left( x \right)~>lo{{g}_{a}}~g\left( x \right)~=>~f\left( x \right)<g\left( x \right)\) при \( \displaystyle 0<a<1\)
Если сказать все простыми словами, то:
Если основание логарифма в неравенстве больше единицы, то знак неравенства сохраняется и для \( \displaystyle f\left( x \right)\) и \( \displaystyle g\left( x \right)\), если же основание логарифма больше нуля и меньше единицы, то знак между \( \displaystyle f\left( x \right)\) и \( \displaystyle g\left( x \right)\) заменяется на противоположный.
Теперь ты понял, почему так сильно отличались решения очень похожих неравенств?
Вся собака зарыта в основаниях!
Теперь ты во всеоружии можешь решать самые разнообразные примеры, щелкая их как орешки (хотя не все орешки имеют мягкую скорлупу).
Вот тебе еще один пример:
\( \displaystyle lo{{g}_{0.2}}\left( {{x}^{2}}+6x+8 \right)>lo{{g}_{0.2}}\left( 5x+10 \right)\).
Ну что же, ты знаешь, что делать: вначале найдем ОДЗ (но здесь у нас будет аж два выражения в нем).
Во-первых \( \displaystyle {{x}^{2}}+6x+8>0\).
Как называется метод, который позволяет решать такие неравенства?
Да! Метод интервалов.
Я просил или нет, повторить его? Кажется, просил. И не зря. Тебя предупреждали, что он может пригодиться в самом неожиданном месте.
Ну ладно, я еще раз напомню, но в первый и последний раз делаю тебе маленькую поблажку.
Первое, что тебе нужно сделать, это найти корни уравнения \( \displaystyle {{x}^{2}}+6x+8=0\), как понимаешь, они равны \( \displaystyle x1=-4,\text{ }x2=-2.\)
Нанесем их на координатную прямую и разобьем ее на три интервала. Найдем знак нашего выражения на каждом из интервалов.
Для этого, как помнишь, я должен выбрать число из какого-нибудь промежутка и подставить его в исходное выражение.
Мне нравится подставлять ноль (не правда ли, удобно?), то есть я найду таким образом знак на крайне правом промежутке.
Выражение в нуле равно восьми, значит знак положительный. Ставлю плюсик. Далее чередую. Получу картинку:
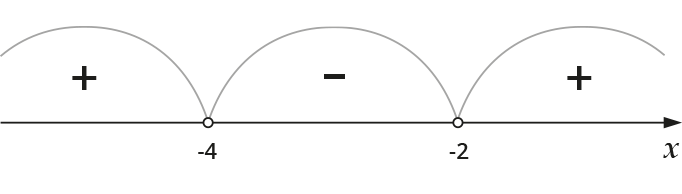
Плюсики меня и интересуют, тогда ОДЗ первого выражения будет множество \( \displaystyle x\in \left( -\infty ;-4 \right)\mathop{\cup }^{}\left( -2;+\infty \right).\)
Второе ОДЗ проще: \( \displaystyle 5x+10>0\). Тут ты и сам справишься и запишешь, что \( \displaystyle x>-2\).
Тогда я пересекаю первое ОДЗ со вторым, получу:
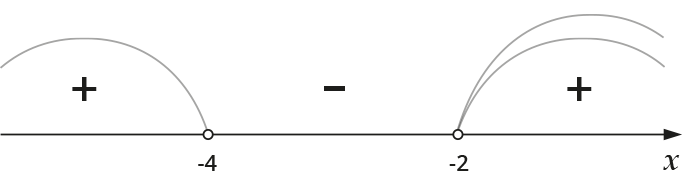
Тогда мое окончательное ОДЗ – есть та область, над которой проходят две дужки – это промежуток \( \displaystyle \left( -2;+\infty \right).\)
Теперь приступим непосредственно к решению неравенства, оно заждалось и неприлично заставлять ждать его еще больше.
\( \displaystyle lo{{g}_{0.2}}\left( {{x}^{2}}+6x+8 \right)>lo{{g}_{0.2}}\left( 5x+10 \right)\)
Поскольку основание у нас \( \displaystyle 0.2<1,\), то ЗНАК НЕРАВЕНСТВА МЫ МЕНЯЕМ!!
Получим:
\( \displaystyle {{x}^{2}}+6x+8<5x+10\)
Упростим:
\( \displaystyle {{x}^{2}}+{x} -2<0\)
И опять применяем метод интервалов. Я пропущу эти выкладки, а ты проведи их и сравни с моим ответом:
\( \displaystyle x\in \left( -2;1 \right).\)
Окончательное решение неравенства – пересечение ОДЗ с только что полученным множеством. Получим:
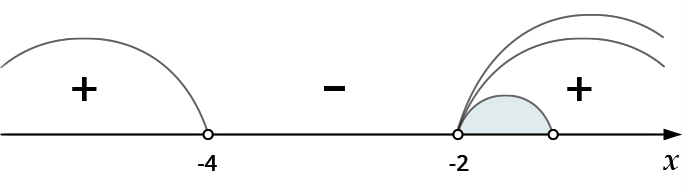
Ответом будет голубой холмик, который ты видишь на картинке.
Ответ: \( x\in \left( -2;1 \right).\)
Алгоритм решения логарифмических неравенств
Теперь давай сформулируем основной алгоритм решения простейших логарифмических неравенств вида \( lo{{g}_{a}}~f\left( x \right)~>~lo{{g}_{a}}~g\left( x \right).~\).
- Находим ОДЗ: \( \left\{ \begin{array}{l}f\left( x \right)>0\\g\left( x \right)>0\end{array} \right.\) (я напомню, что знак системы (фигурная скобка) означает, что должны выполняться одновременно оба неравенства;
- Смотрим на основание: если \( a>1\), то решаем неравенство \( f\left( x \right)>g\left( x \right).\) Если же \( 0<a<1\), то решаем \( f\left( x \right)<g\left( x \right)\);
- Совмещаем полученное решение неравенства из пункта 2 с нашим ОДЗ из пункта 1;
Те же самые правила применимы и к трем другим видам логарифмических неравенств.
Но ты заметил, что я немного «кривил душой»? Во-первых, кто сказал, что всегда ясно однозначно, какое значение принимает основание. Никто этого не говорил…
Основание также может быть переменным, например, \( a=2x+1\). И тогда нам нужно уже рассматривать отдельно 2 случая: когда оно больше единицы и когда лежит между нулем и единицей.
Однако этому «сложному» случаю будет посвящена следующая статья, где он рассматривается отдельно.
В общем случае, внешний вид логарифмических неравенств может существенно отличаться от простейших. В таком случае что мы с тобой должны сделать вначале?
Верно, привести неравенство к виду простейшего. И мы обязательно будем это делать, но самую малость попозже.
А пока давай немного потренируемся в решении самых базовых логарифмических неравенств.
Пример №1
- \( lo{{g}_{0.3}}\left( x+4 \right)>lo{{g}_{0.3}}\left( {{x}^{2}}+2{x} -2 \right)\)
Решение:
Вначале найдем ОДЗ:
\( \left\{ \begin{array}{l}x+4>0\\{{x}^{2}}+2{x} -2>0\end{array} \right.\)
Из первого неравенства следует, что \( x>-4\).
Второе решим методом интервалов, который я уже успел неоднократно применить выше (и буду применять впредь!).
Пример №2
- \( lo{{g}_{0.3}}\left( -x+2 \right)\le lo{{g}_{0.3}}\left( 2{x} -2 \right)\)
Решение:
Второй пример полегче: здесь нам с тобой не требуется решать никаких квадратичных неравенств. Так что приступим:
ОДЗ:
\( \left\{ \begin{array}{l}-x+2>0\\2{x} -2>0\end{array} \right.\)
Откуда:
\( \left\{ \begin{array}{l}x<2\\x>1\end{array} \right.\)
Тогда мы получаем очень простое ОДЗ:
\( x\in \left( 1;2 \right)\)
Теперь решение самого неравенства:
Пример №3
- \( lo{{g}_{2}}\left( 4x+12 \right)\le lo{{g}_{2}}\left( 10 \right)\)
Третье неравенство еще проще предыдущего!
ОДЗ здесь еще проще: оно состоит всего из одного неравенства: \( 4x+12>0,\) решением которого будет промежуток \( x\in \left( -3;+\infty \right).\)
Так как \( 2>1\), то исходное неравенство равносильно следующему:
Кстати, обрати пристальное внимание на первый пример (хотя и на второй тоже). Посмотри, тебя ничего не смущает?
Видишь, что решение неравенства \( {{x}^{2}}+2{x} -2>0\) никак не вошло в наш окончательный ответ? И это неслучайно.
Поскольку исходное неравенство равносильно тому, что \( x+4<{{x}^{2}}+2{x} -2,~\) но при этом \( x+4>0\), то второе выражение и подавно автоматически будет больше нуля, так как по условию оно строго больше.
После того как ты разобрался в решении этих трех примеров, я думаю, что ты готов к осознанию некоторого более сложного правила решения логарифмических неравенств.
Правило, позволяющее экономить время при решении логарифмических неравенств
Решение логарифмического неравенства вида \( lo{{g}_{a}}~f\left( x \right)<lo{{g}_{a}}~g\left( x \right)\) равносильно решению следующих систем:
\( 0<a<1:\left\{ \begin{array}{l}f\left( x \right)>g\left( x \right)\\g\left( x \right)>0\end{array} \right.\)
\( a>1:\left\{ \begin{array}{l}f\left( x \right)<g\left( x \right)\\f\left( x \right)>0\end{array} \right.\)
Неравенство \( lo{{g}_{a}}~f\left( x \right)>lo{{g}_{a}}~g\left( x \right)\) в каждом из двух случаев сводится к одной из систем:
\( 0<a<1:\left\{ \begin{array}{l}f\left( x \right)<g\left( x \right)\\f\left( x \right)>0\end{array} \right.\)
\( a>1:\left\{ \begin{array}{l}f\left( x \right)>g\left( x \right)\\g\left( x \right)>0\end{array} \right.\)
Использование данного правила позволит тебе экономить время и силы при нахождении ОДЗ, так как оно уменьшает количество неравенств, которые нам с тобой нужно решить.
Но для использования данного правила тебе нужно быть еще более внимательным.
Ничего страшного, если ты сразу не научишься применять его на практике!
Ты всегда можешь следовать уже «отлаженной» схемой, которую я разбирал выше, а потом, когда почувствуешь себя увереннее, сможешь пользоваться и этим правилом!
Теперь давай перейдем к более общему случаю логарифмических неравенств.
Общий случай логарифмических неравенств
…когда его левая или правая часть (или может так выйти, что и обе разом) не приведены сразу к виду простейшего логарифмического неравенства.
Например:
\( \displaystyle lo{{g}_{2}}\left( {{x}^{2}}+4x+3 \right)>3\)Мы с тобой видим, что с левой частью все в порядке – она представляет собой логарифмическое выражение. Не в порядке у нас правая часть – она есть просто число три.
Что же нам теперь делать?
Ну, во-первых, не отчаиваться. А, во-вторых, ты не представляешь, насколько может быть продуктивным такое на первый взгляд бесполезное действие, как умножение на единицу.
\( \displaystyle 3=3\cdot 1\).
Зачем я это сделал, как ты думаешь? А вот зачем: я (и ты тоже) помню, что для любого положительного числа \( \displaystyle a\) имеет место равенство:
\( \displaystyle lo{{g}_{a}}a=1\)Тебе, я надеюсь, очевидно, почему это так? Да все потому, что а нужно возвести в первую степень, чтобы само а и получить в итоге. Тогда я запишу, что
\( \displaystyle 3=3\cdot lo{{g}_{2}}2.\)Сам подумай, почему я выбрал два в качестве основания логарифма. Теперь я воспользуюсь простым свойством:
\( \displaystyle r\cdot lo{{g}_{a}}b=lo{{g}_{a}}{{b}^{r}}\)И получу, что: \( \displaystyle 3=3\cdot lo{{g}_{2}}2=lo{{g}_{2}}{{2}^{3}}=lo{{g}_{2}}8.\)
И наше неравенство превратилось в стандартное
\( \displaystyle lo{{g}_{2}}\left( {{x}^{2}}+4x+3 \right)>lo{{g}_{2}}8\)Которое ты и без моей помощи сам прекрасно решишь. Давай сверим ответы. У меня получилось, что \( \displaystyle x\in \left( -\infty ;-5 \right)\mathop{\cup }^{}\left( 1;+\infty \right)\), а у тебя?
Вот видишь, каким волшебным может быть обычное умножение на единицу!!
Давай решим еще примеры на логарифмические неравенства.
Пример №4
\( \displaystyle 2+lo{{g}_{2}}\sqrt{x+1}>1-lo{{g}_{\frac{1}{2}}}\sqrt{4-{{x}^{2}}}\).
Решение:
Я опять представлю число \( \displaystyle 2\) как \( \displaystyle 2\cdot lo{{g}_{2}}2=lo{{g}_{2}}4\), единицу как \( \displaystyle lo{{g}_{2}}2\), а в выражении \( \displaystyle lo{{g}_{1/2}}\sqrt{4-{{x}^{2}}}\) воспользуюсь тем, что
\( \displaystyle 1/r\cdot lo{{g}_{a}}b=lo{{g}_{{{a}^{r}}}}b\) (все те же пресловутые свойства логарифмов!!)
Так как \( \displaystyle \frac{1}{2}={{2}^{-1}}\) (свойства степени!!), то исходное неравенство преобразуется вот к такому:
\( \displaystyle lo{{g}_{2}}4+lo{{g}_{2}}\sqrt{x+1}>lo{{g}_{2}}2-\left( \frac{1}{-1} \right)lo{{g}_{2}}\sqrt{4-{{x}^{2}}}\) или
\( \displaystyle lo{{g}_{2}}4+lo{{g}_{2}}\sqrt{x+1}>lo{{g}_{2}}2+lo{{g}_{2}}\sqrt{4-{{x}^{2}}}\)Теперь я воспользуюсь тем, что
\( \displaystyle lo{{g}_{a}}b+lo{{g}_{a}}c=lo{{g}_{a}}\left( bc \right)\), тогда я получу:
\( \displaystyle lo{{g}_{2}}4\sqrt{x+1}>lo{{g}_{2}}2\sqrt{4-{{x}^{2}}}\)Вы позволите мне воспользоваться нашим новым правилом решения логарифмических неравенств?
Ясно, что так как \( \displaystyle 2>1\), то наше неравенство будет равносильно такому:
\( \displaystyle 4\sqrt{x+1}>2\sqrt{4-{{x}^{2}}}\)Из того, что \( \displaystyle 2\sqrt{4-{{x}^{2}}}>0\) и из того, что это выражение меньше, чем \( \displaystyle 4\sqrt{x+1}\), будет автоматически следовать, что и подавно \( \displaystyle 4\sqrt{x+1}>0\) и нам не надо учитывать это в ОДЗ.
Еще раз!!!
Если тебе не очень пока понятно это утверждение, ты всегда можешь воспользоваться построением «полного» ОДЗ, результат будет тоже правильным!
Тогда мое исходное неравенство будет равносильно следующей системе:
\( \displaystyle \left\{ \begin{array}{l}\sqrt{4-{{x}^{2}}}>0\\4\sqrt{x+1}>2\sqrt{4-{{x}^{2}}}\end{array} \right.\)Первое имеет решение: \( \displaystyle x\in \left( -2;2 \right)\)
А второе: \( \displaystyle x\in \left( -\infty ;-4 \right)\mathop{\cup }^{}\left( 0;+\infty \right)\)
Пересекая первое решение со вторым пишу ответ: \( \displaystyle x\in \left( 0;2 \right)\)
Пример №5
Теперь я усложню тебе задачу: каждый раз я буду сводить неравенство к простейшему виду, а уже решать будешь ты сам.
Готов? Начнем!
\( \displaystyle lg{{\left( x+1 \right)}^{2}}>0\)Решение:
Во-первых, что за зверь такой \( \displaystyle lg\)? Слышал о нем раньше? \( \displaystyle lg\left( x \right)\) – это десятичный логарифм, то есть логарифм с основанием \( \displaystyle 10\). Иначе его можно написать в следующем виде: \( \displaystyle lg\left( x \right)=lo{{g}_{10}}x\).
Во-вторых, что нам делать с нулем справа? А нужно всего лишь вспомнить, что
\( \displaystyle lo{{g}_{a}}1=0\) для любого \( \displaystyle a>0\)!!!!
Попробуй сам объяснить, почему это так.
Теперь я перехожу от исходного неравенства к простейшему:
Самостоятельная работа
- \( \displaystyle lo{{g}_{5}}\left( 1+x \right)>lo{{g}_{5}}\left( -x \right)\)
- \( \displaystyle lo{{g}_{0.5}}\left( 2x+5 \right)\ge -2\)
- \( \displaystyle 3\ge lo{{g}_{5}}{{x}^{3}}\)
- \( \displaystyle lo{{g}_{2}}\left( {{x}^{2}}-7x+18 \right)\le 3\)
- \( \displaystyle lg\sqrt{{x} -1}<-1\)
Я продолжу лениться: буду лишь приводить каждое из неравенств к простейшему виду и давать ответ, с которым ты будешь сравнивать свои результаты:
Решения:
Средний уровень
В начальном уровне теории мы с тобой разобрали, как решать простейшие логарифмические неравенства вида:
\( \displaystyle {{\log }_{a}}f(x)<{{\log }_{a}}g(x)\)Мы сформулировали основное правило их решения, которое гласит, что:
решение логарифмического неравенства вида \( \displaystyle {{\log }_{a}}f(x)<{{\log }_{a}}g(x)\)
равносильно решению следующих систем:
- \( \displaystyle 0<a<1:\left\{ \begin{array}{l}f(x)>g(x)\\g(x)>0\end{array} \right.\)
- \( \displaystyle a>1:\left\{ \begin{array}{l}f(x)<g(x)\\g(x)>0\end{array} \right.\)
Неравенство \( \displaystyle {{\log }_{a}}f(x)>{{\log }_{a}}g(x)\) в каждом из двух случаев сводится к одной из систем:
- \( \displaystyle 0<a<1:\left\{ \begin{array}{l}f(x)<g(x)\\f(x)>0\end{array} \right.\)
- \( \displaystyle a>1:\left\{ \begin{array}{l}f(x)>g(x)\\g(x)<0\end{array} \right.\)
Также мы привели несколько примеров таких неравенств, которые некоторыми (не очень обременительными) процедурами приводятся к простейшему виду.
Так что при изложении дальнейшего материала в этой статье, я буду уже предполагать, что с базовыми навыками решения логарифмических неравенств ты знаком.
Однако за бортом у нас осталось несколько случаев…
Более сложные логарифмические неравенства
- А что, если неравенство нельзя привести к простейшему виду, описанному выше?
- А что, если основание у логарифма не постоянное число, а некоторая функция, зависящая от переменной \( \displaystyle x\)?
- А что, если основания в логарифмических неравенствах разные?
Ответы на эти вопросы дадут нам с тобой ключи, необходимые для решения более сложных логарифмических неравенств, нежели простейшие.
Я начну с первого метода, который мы используем не только при решении неравенств, но также и при отыскании корней некоторых уравнений: метод замены переменной.
Давай рассмотрим следующий пример:
\( \displaystyle {{\log }_{2}}^{2}x+{{\log }_{0,5}}x > 12\)Что мне видно сразу? А то, что \( \displaystyle 0,5={{2}^{-1}}\), и поскольку
\( \displaystyle \frac{1}{r}\cdot {{\log }_{a}}b={{\log }_{{{a}^{r}}}}b\),
То я перейду к равносильному неравенству вида:
\( \displaystyle {{\log }_{2}}^{2}x-{{\log }_{2}}x>12\)Мы с тобой видим, что такое неравенство уже нельзя назвать элементарным. Почему? Да потому, что логарифм в него входит во второй степени.
А разве такие неравенства мы называли элементарными? Вот и я думаю, что нет. Как же нам поступить?
Вот еще один пример на замену переменных в неравенстве:
\( \displaystyle \frac{lgx-1}{\lg x\cdot (\lg x+1)}>0\)Мне кажется, здесь опять замена напрашивается сама собой: \( \displaystyle t=\lg x\)
Тогда я получу:
Логарифмическое неравенство с переменным основанием
\( \displaystyle {{\log }_{h(x)}}f(x)V{{\log }_{h(x)}}g(x)\) (1)
где \( \displaystyle h(x),g(x),f(x)\) – некоторые функции, зависящие от \( \displaystyle x\), а \( \displaystyle V\) – один из знаков: \( \displaystyle >,<,\le ,\ge \). Хитрые математики, когда видят логарифмы, сразу же стараются от них избавиться, переходя к равносильным неравенствам.
В частности для неравенства выше равносильным будет вот такое:
\( \displaystyle \left\{ \begin{array}{l}(f(x)-g(x))\cdot (h(x)-1)V0\\f(x)>0\\g(x)>0\\h(x)>0\\h(x)\ne 1\end{array} \right.\)Бывают еще более печальные случаи, когда неравенство имеет вид:
\( \displaystyle {{\log }_{f(x)}}h(x)V{{\log }_{g(x)}}h(x)\), (2)
то есть представляет собой логарифмическое неравенство с РАЗНЫМИ основаниями, но одинаковыми выражениями «сверху». Для него равносильной системой будет следующая:
\( \displaystyle \left\{ \begin{array}{l}(f(x)-1)(g(x)-1)\cdot (h(x)-1)(g(x)-f(x))V0\\f(x)>0\\g(x)>0\\h(x)>0\\g(x)\ne 1\\f(x)\ne 1\end{array} \right.\)Все становится все ужаснее и ужаснее, правда? Но ничего, скоро мы перейдем к примерам (очень важным!) и все встанет на свои места!
Вот последний вид «сложного» неравенства:
\( \displaystyle \text{lo}{{\text{g}}_{\text{t}\left( \text{x} \right)}}\text{f}\left( \text{x} \right)\cdot \text{lo}{{\text{g}}_{\text{h}\left( \text{x} \right)}}\text{g}\left( \text{x} \right)\text{V }\!\!~\!\!\text{ }0\) (3)
Ему равносильна следующая система:
\( \displaystyle \left\{ \begin{array}{l}(f(x)-1)(t(x)-1)\cdot (h(x)-1)(g(x)-1)V0\\f(x)>0\\g(x)>0\\h(x)>0\\t(x)>0\\t(x)\ne 1\\h(x)\ne 1\end{array} \right.\)Представленный метод решения неравенств (1), (2), (3) говорит нам о том, как от сложного логарифмического неравенства (но одного!) перейти к простым неравенствам (но к целой системе!).
По сути этот метод позволяет одно сложное свести к системе простых. Этот метод получил название..
Метод декомпозиции (рационализации)
На самом деле, можно и не запоминать все формулы в каждой системе. Все, кроме первой – это просто-напросто ОДЗ (ну в самом деле, просто взгляни на них), а первое – это так называемое условие сохранения знака.
К нему ты всегда можешь прийти, рассматривая случаи, когда \( \displaystyle 0<h\left( x \right)<1\) и когда \( \displaystyle h\left( x \right)>1\).
В частности, если \( \displaystyle 0<h\left( x \right)<1\), то неравенство \( \displaystyle lo{{g}_{h\left( x \right)}}f\left( x \right)>~lo{{g}_{h\left( x \right)}}g\left( x \right)\) влечет за собой \( \displaystyle f\left( x \right)<g\left( x \right)\).
С другой стороны, так как \( \displaystyle h\left( x \right)-1<0\) неравенство \( \displaystyle \left( f\left( x \right)-g\left( x \right) \right)\left( h\left( x \right)-1 \right)>0\) имеет место только тогда, когда \( \displaystyle f\left( x \right)-g\left( x \right)<0\) или \( \displaystyle f\left( x \right)<g\left( x \right)\).
Получили, что при \( \displaystyle 0<h\left( x \right)<1\) неравенства \( \displaystyle lo{{g}_{h\left( x \right)}}f\left( x \right)>~lo{{g}_{h\left( x \right)}}g\left( x \right)\) и \( \displaystyle \left( f\left( x \right)-g\left( x \right) \right)\left( h\left( x \right)-1 \right)>0\) равносильны (учитывая, конечно, ОДЗ). Аналогично ты можешь получить, что эти же неравенства будут равносильны и при \( \displaystyle h\left( x \right)>1\).
Но если ты и эту формулу забыл, то ничего страшного, просто придется дольше поработать. Ты всегда можешь решить логарифмическое неравенство, опираясь только на определение логарифмической функции. В частности, неравенство
\( \displaystyle lo{{g}_{h\left( x \right)}}f\left( x \right)>~lo{{g}_{h\left( x \right)}}g\left( x \right)\)Равносильно следующей системе:
\( \displaystyle \left\{ \begin{array}{l}\left[ \begin{array}{l}\left\{ \begin{array}{l}f(x)>g(x)\\h(x)>1\end{array} \right.\\\left\{ \begin{array}{l}f(x)<g(x)\\0<h(x)<1\end{array} \right.\end{array} \right.\\f(x)>0\\g(x)>0\\h(x)>0\\h(x)\ne 1\end{array} \right.\)Где сложное условие \( \displaystyle \left( f\left( x \right)-g\left( x \right) \right)\left( h\left( x \right)-1 \right)>0\) я заменил совокупностью из двух систем.
Решение любого сложного логарифмического уравнения я рекомендую начинать с ОДЗ.
В некоторых случаях это позволит тебе не решать одну из двух систем, поскольку будет заведомо известно, что ее решение не лежит в ОДЗ.
Ты уже в трепете перед этими сложными формулами? Я тебя понимаю. Однако, все, что я могу сказать: аппетит приходит во время еды.
И большинство «монструозных» задач сложного уровня, имеющих в своем составе логарифмы, сводятся в конечном счете к одному из неравенств вида (1)-(3), либо решаются при помощи некоторой замены переменной.
Я не хочу быть более голословным, поэтому перейду к примерам прямо сейчас. Обрати внимание, все следущие примеры взяты из ЕГЭ предыдущих лет!
Пример из ЕГЭ предыдущих лет №1 (на хорошую замену)
\( \displaystyle lo{{g}_{x}}3+2lo{{g}_{3x}}3-6lo{{g}_{9x}}3\le 0\)Решение:
Во многих случаях, при решении «сложных» неравенств, может полезной оказаться одна из следующих формул:
\( \displaystyle lo{{g}_{a}}b=\frac{lo{{g}_{c}}b}{lo{{g}_{c}}a}\), \( \displaystyle lo{{g}_{a}}b=\frac{1}{lo{{g}_{b}}a}\).
В данном случае мне удобно воспользоваться второй формулой. Понимаешь, почему? Да все потому, что все три логарифма содержат в себе тройку «наверху»!!
Если я преобразую исходное неравенство, то у меня получится:
Пример из ЕГЭ предыдущих лет №2 (на «сложную» замену переменной)
\( \displaystyle \frac{lo{{g}_{{{7}^{x+3}}}}49}{lo{{g}_{{{7}^{x+3}}}}\left( -49x \right)}\le \frac{1}{lo{{g}_{7}}lo{{g}_{\frac{1}{7}}}{{7}^{x}}}\)Решение:
Вначале найдем ОДЗ:
\( \displaystyle \left\{ \begin{array}{l}x\ne -1\\x\ne -\frac{1}{49}\\x\ne -3\\x<0\end{array} \right.\)Вы можете оспорить второе выражение системы. В самом деле, откуда оно берется?
А во всем виновато соотношение: \( \displaystyle lo{{g}_{a}}b=\frac{lo{{g}_{c}}b}{lo{{g}_{c}}a}\), которое применимо к нашему случаю даст:
\( \displaystyle \frac{lo{{g}_{{{7}^{x+3}}}}49}{lo{{g}_{{{7}^{x+3}}}}\left( -49x \right)}=lo{{g}_{\left( -49x \right)}}49=\frac{1}{lo{{g}_{49}}\left( -49x \right)}=\frac{1}{1+lo{{g}_{49}}\left( -x \right)}=\frac{2}{2+lo{{g}_{7}}\left( -x \right)}\)Второе выражение преобразуем вот так:
\( \displaystyle \frac{1}{lo{{g}_{7}}lo{{g}_{\frac{1}{7}}}{{7}^{x}}}=\frac{1}{lo{{g}_{7}}\left( -lo{{g}_{7}}{{7}^{x}} \right)}=\frac{1}{lo{{g}_{7}}\left( -xlo{{g}_{7}}7 \right)}=\frac{1}{lo{{g}_{7}}\left( -x \right)}.\)Тогда наше неравенство преобразуется к вот такому виду:
\( \displaystyle \frac{2}{2+lo{{g}_{7}}\left( -x \right)}\le \frac{1}{lo{{g}_{7}}\left( -x \right)}.\)Ага, теперь замена напрашивается сама собой!!
Пример из ЕГЭ предыдущих лет №3 (неравенство с переменным основанием)
\( \displaystyle lo{{g}_{{{x}^{2}}+1}}10<1\)Решение:
Мы можем преобразовать его к виду:
\( \displaystyle lo{{g}_{{{x}^{2}}+1}}10<lo{{g}_{{{x}^{2}}+1}}\left( {{x}^{2}}+1 \right)\)Тогда, наше неравенство имеет вид (1). Я напомню, что в этом случае решить наше неравенство – это все равно, что решить вот такую систему:
Пример из ЕГЭ предыдущих лет №4
\( \displaystyle lo{{g}_{12{{x}^{2}}-41x+35}}\left( 3-x \right)\le lo{{g}_{2{{x}^{2}}-5x+3}}\left( 3-x \right)\)Решение:
Данное неравенство имеет вид (2). Значит перейдем к равносильной ему системе:
\( \displaystyle \left\{ \begin{array}{l}\left( 12{{x}^{2}}-41x+34 \right)\left( 2-x \right)\left( 2{{x}^{2}}-5x+2 \right)\left( 10{{x}^{2}}-36x+32 \right)\le 0\\12{{x}^{2}}-41x+35>0\\2{{x}^{2}}-5x+3>0\\3-x>0\\12{{x}^{2}}-41x+35\ne 1\\2{{x}^{2}}-5x+3\ne 1\end{array} \right.\)Теперь твоя цель – решить методом интервалов каждое из указанных в системе неравенств, а затем найти область их пересечения. Я самоустраняюсь от этой (хоть и тривиальной, но достаточно трудоемкой) задачи, и доверяю ее тебе. Окончательный ответ будет вот таким:
\( \displaystyle \left( -\infty;\frac{1}{2}\right)\mathop{\cup }^{}\left(\frac{3}{2}; \frac{8}{5}\right]\)Итак….
В данной статье я постарался объяснить тебе подходы к решению одних из самых трудных задач, встречающихся в школьном курсе – решению логарифмических неравенств.
Я надеюсь, чтение и разбор примеров оказались для тебя полезными и время ты потратил не зря. Опять-таки повторюсь: чтобы освоить методы решения, тебе нужно совсем немного: всего три вещи: практика, практика и практика.
Мини-максный метод решения логарифмических неравенств
В дополнение к уже изложенному материалу (который, увы, не охватывает и не может охватывать весь спектр способов решения логарифмических неравенств), я рассмотрю еще один способ, который может быть полезен там, где ничего больше не помогает (но опять-таки, я сразу оговорюсь, что изложенный метод не является панацеей).
Данный метод будет основан на некоторых свойствах логарифмической функции: на ее монотонности и на наибольших и наименьших значениях на интервале ее существования.
Прежде чем приступать к рассмотрению метода, я напомню тебе, что такое монотонность функции:
Определение монотонности функции:
\( \displaystyle f\left( x \right)\) монотонно возрастает на \( \displaystyle \left[ a,b \right]\), если для любых \( \displaystyle {{x}_{1}},{{x}_{2}}\) из этого промежутка из того, что \( \displaystyle {{x}_{1}}<{{x}_{2}}\) следует, что \( \displaystyle f\left( {{x}_{1}} \right)<f\left( {{x}_{2}} \right)\) и наоборот, из того, что \( \displaystyle {{x}_{1}}>{{x}_{2}}\) следует, что \( \displaystyle f\left( {{x}_{1}} \right)>f\left( {{x}_{2}} \right).\)
Определение:
\( \displaystyle f\left( x \right)\) монотонно убывает на \( \displaystyle \left[ a,b \right]\), если для любых \( \displaystyle {{x}_{1}},~{{x}_{2}}\) из этого промежутка из того, что \( \displaystyle {{x}_{1}}<{{x}_{2}}\) следует, что \( \displaystyle f\left( {{x}_{1}} \right)>f\left( {{x}_{2}} \right)\) и наоборот, из того, что \( \displaystyle {{x}_{1}}>{{x}_{2}}\) следует, что \( \displaystyle f\left( {{x}_{1}} \right)<f\left( {{x}_{2}} \right).\)
Простые рисунки иллюстрируют эти определения:
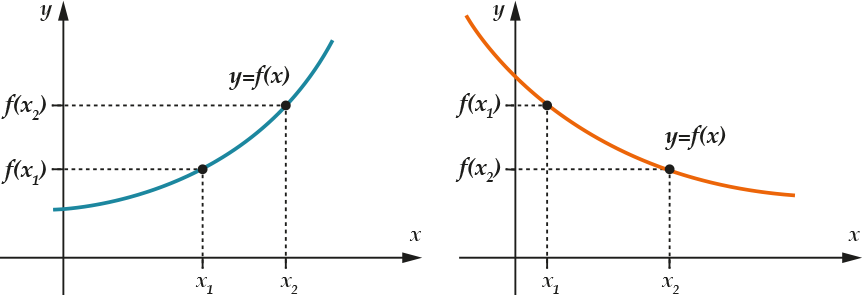
Функция на рисунке слева – монотонно возрастающая, а справа – монотонно убывающая. Теперь обратимся к логарифмической функции \( \displaystyle f(x)=lo{{g}_{a}}x4\), известно, что выполняется следующая:
Теорема: если \( \displaystyle a>1\), то функция \( \displaystyle f\left( x \right)=~lo{{g}_{a}}x\) является монотонно возрастающей, если \( \displaystyle 0<a<1\), то функция \( \displaystyle f\left( x \right)=~lo{{g}_{a}}x\) является монотонно убывающей.
На рисунке приведены примеры монотонно возрастающей и монотонно убывающей логарифмической функции. Теперь я могу приступать к рассмотрению одного из приемов решения логарифмических неравенств.
Рассмотренный здесь метод называется мини-максным.
Я думаю, что ты понимаешь, от каких слов произошло такое название? Верно, от слов минимум и максимум. Кратко метод можно представить в виде:
\( \displaystyle \left\{ \begin{array}{l}f\left( x \right)\le g\left( x \right)\\f\left( x \right)\ge A\\g\left( x \right)\le A\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}f\left( x \right)=g\left( x \right)\\f\left( x \right)\ge A\\g\left( x \right)\le A\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}f\left( x \right)=A\\g\left( x \right)=A\end{array} \right.\)Иногда данный метод позволяет решать на первый взгляд «безнадежные» неравенства вроде
\( \displaystyle lo{{g}_{2}}\left( 6x-{{x}^{2}}-7 \right)\ge {{7}^{\left| x-3 \right|}}\)Давай введем в рассмотрение две функции
\( \displaystyle f\left( x \right)=~lo{{g}_{2}}\left( 6x-{{x}^{2}}-7 \right)\), \( \displaystyle g\left( x \right)=~{{7}^{\left| x-3 \right|}}\)
Найдем для каждой из них область значений \( \displaystyle E\left( f \right),E\left( g \right)\):
Пусть \( \displaystyle t=6x-{{x}^{2}}-7\)
\( \displaystyle 6x-{{x}^{2}}-7=-{{\left( x-3 \right)}^{2}}+2,~\) то есть \( \displaystyle t\le 2\), с другой стороны, по определению логарифма \( \displaystyle t>0\).
Так как \( \displaystyle y=f\left( t \right)\) возрастает на \( \displaystyle \left( 0;2 \right]\).
Причем, при \( \displaystyle t\) стремящемся к нулю, \( \displaystyle f\left( t \right)\) стремится к минус бесконечности (смотри рисунок выше), а при \( \displaystyle t=2,~f\left( t \right)=f\left( 2 \right)=1\).
Таким образом, область значений \( \displaystyle f(x)\) есть множество:
\( \displaystyle E\left( f \right)=\left( -\infty ;1 \right].\)Теперь найдем область значений \( \displaystyle g(x)\): вновь введем замену \( \displaystyle z=\left| x-3 \right|,\) \( \displaystyle z\ge 0\) (по определению модуля), так как \( \displaystyle g\left( z \right)={{7}^{z}}\) возрастает на всей числовой прямой, то наименьшее значение \( \displaystyle g\left( z \right)\) при \( \displaystyle z\ge 0\) достигается при \( \displaystyle z=0\), \( \displaystyle g\left( 0 \right)=1\), \( \displaystyle g\left( z \right)>1\) при \( \displaystyle z>0\). Таким образом:
\( \displaystyle E\left( g \right)=\left[ 1;+\infty \right).\)Воспользуемся мини-максным методом: он говорит нам о том, что решение неравенства может иметь место только при
\( \displaystyle f\left( x \right)=g\left( x \right)=A\). В нашем случае \( \displaystyle A=1.\)
Тогда \( \displaystyle f\left( x \right)=1\) эквивалентно: \( \displaystyle lo{{g}_{2}}\left( 6x-{{x}^{2}}-7 \right)=1\) а из \( \displaystyle g\left( x \right)=1\) получится \( \displaystyle {{7}^{\left| x-3 \right|}}=1.\) Первое уравнение имеет корень: \( \displaystyle x=3\), это же число является и корнем второго уравнения. Тогда наше исходное неравенство имеет место только при \( \displaystyle x=3\).
Вот такой пример (позаковырестее) я предлагаю решить тебе самому:
\( \displaystyle \left\{ \begin{array}{l}lo{{g}_{\frac{1}{3}}}\left( 3+\left| sinx \right| \right)\ge {{2}^{\left| x \right|}}-2\\lo{{g}_{\left( x+2.5 \right)}}{{\left( \frac{x-5}{2x-3} \right)}^{2}}>0\end{array} \right.\)Давай посмотрим, что у нас получилось:
Я начну с анализа первого неравенства: Слева у меня стоит монотонно убывающая функция, а справа – монотонно возрастающая. Вначале мы разберемся с \( \displaystyle f\left( x \right)=lo{{g}_{\frac{1}{3}}}\left( 3+\left| sinx \right| \right)\), пусть \( \displaystyle t=3+\left| sinx \right|\), тогда из того, что \( \displaystyle 0\le \left| sinx \right|\le 1\), следует, что \( \displaystyle 3\le t\le 4\).
Функция \( \displaystyle f\left( t \right)\) является монотонно убывающей при \( \displaystyle 3\le t\le 4\), тогда своего наибольшего значения она достигает при \( \displaystyle t=3\), а наименьшего – при \( \displaystyle t=4\).
Тогда:
\( \displaystyle -lo{{g}_{3}}4\le f\left( t \right)\le -1\)Теперь рассмотрим \( \displaystyle g\left( x \right)={{2}^{\left| x \right|}}-2\), сделаем замену \( \displaystyle t=\left| x \right|,~t\ge 0\). Тогда \( \displaystyle g\left( t \right)={{2}^{t}}-2\) монотонно возрастает и наименьшего значения достигает при \( \displaystyle t=0.\) Это значение будет равно \( \displaystyle g\left( 0 \right)=-1.\) При \( \displaystyle t>0~g\left( t \right)>-1.\)
Вновь воспользуемся мини-максным методом. В данном случае первое неравенство может иметь место только при \( \displaystyle f\left( x \right)=g\left( x \right)=-1\). Ясно, что первое уравнение имеет бесконечное количество корней, задаваемых формулой
\( \displaystyle x=\pi n,~n\in Z.\)Тогда как второе имеет только один корень \( \displaystyle x=0\). Ясно, что при подстановке \( \displaystyle n=0\) в формулу корней первого уравнения, я получу, что \( \displaystyle x=0\). Тогда первое неравенство выполняется только при \( \displaystyle x=0\).
Что же теперь? Нужно ли нам решать второе неравенство? А смысл? Ведь если оно и имеет решение, то нам нужно будет его пересекать с тривиальным решением первого неравенства. Так не проще ли нам подставить во второе неравенство \( \displaystyle 0\) и проверить, имеет ли оно при этом место? Я думаю, что это не представляет никакого труда.
\( \displaystyle lo{{g}_{\left( 0+2.5 \right)}}{{\left( \frac{0-5}{2*0-3} \right)}^{2}}=lo{{g}_{2.5}}\left( \frac{25}{9} \right)>lo{{g}_{2.5}}1>0\)Тогда с чистой совестью записываю ответ: \( \displaystyle x=0\).
Конечно, мини-максный метод является не единственным методом решения сложных логарифмических неравенств, однако он в полной мере демонстрирует мощь «функционального» подхода к решению неравенств (кстати, и уравнений тоже).
Бонус: Вебинар по ЕГЭ №15 — логарифмические и тригонометрические
Подготовка к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Здравствуйте, у вас опечатка в системе для равносильного перехода третьего вида сложного неравенства. В первой строчке у вас дублируется скобка (g(x) — 1). Там последней должна быть (t (x) — 1). Проверьте, пожалуйста.
Спасибо, Ксения!
Добрый вечер! У меня возник вопрос. В одном из примеров вы пишете log0.3(−x+2)≤log0.3(2x−2)
Как и в предыдущем примере я сменяю знак, так как 0.3<1, получу:
−x−2≥2x−2
−3x≥0
x≤0
Объясните, пожалуйста, почему поменялся знак? Было (−x+2), а стало −x−2?
Ошиблись. Там знак не меняется.
у вас ответ неверный в последнем примере на переменное основание….верный: x<1/2, 3/2<x<=8/5…
Некоторые отзывы об этой статье за прошлые годы:
Анна
08 января 2018
Замечательный сайт, спасибо!
Ксения
16 января 2018
Очень крутой сайт. Все максимально просто и понятно написано. Теперь я действительно все понимаю.
Savva Muzurov
26 февраля 2018
Прекрасный сайт ) все предельно ясно и понятно )
Рашид
25 февраля 2019
Спасибо за сайт! Вроде разобрался, только надо будет выучить формулы для решения логарифмов с переменными основаниями. Админы класные)
Катька
24 марта 2019
Благодаря вашему сайту и данной статье я смогла сформулировать предложения для курсовой). Конечно, эту тему я знаю, но почему бы не подкрепить свои знания?) Автор, вы ничего не упустили, спасибо вам!)
людмила евгеньевна
13 августа 2019
спасибо за обстоятельность и легкость подачи. вспомнила логарифмы через 45 лет после окончания школы, сейчас учусь онлайн ,мне это помогло вспомнить даже то чего не знала
Марина
26 февраля 2020
Очень интересно и понятно рассказано. Спасибо огромное!!!