Метод интервалов
Метод интервалов тебе просто необходимо понять и знать его как свои пять пальцев!
Хотя бы потому, что он применяется для решения рациональных неравенств.
И потому, что, зная этот метод как следует, решать эти неравенства на удивление просто.
Чуть позже раскрою тебе пару секретов, как сэкономить время на решении этих неравенств.
Ну что, заинтриговал? Тогда поехали!
Метод интервалов — коротко о главном
Метод интервалов применяется для решения рациональных неравенств.
Он заключается в определении знака произведения по знакам сомножителей на различных промежутках.
Алгоритм решения рациональных неравенств методом интервалов:
- Переносим все в левую часть, справа оставляем только ноль;
- Находим ОДЗ;
- Наносим на ось все корни неравенства;
- Берем произвольный \( x\) из одного из промежутков и определяем знак в интервале, к которому относится корень, чередуем знаки, обращая внимание на корни, повторяющиеся в неравенстве несколько раз, от четности или нечетности количества раз их повторения зависит, меняется знак при прохождении через них или нет;
- В ответ пишем интервалы, соблюдая выколотые и не выколотые точки (смотри ОДЗ), ставя необходимые виды скобок между ними.
Суть метода интервалов
Суть метода в разложении неравенства на множители (повтори тему «Разложение на множители»), определении ОДЗ и знака сомножителей.
Сейчас все поясню.
Возьмем самый простенький пример: \( (x+1)\cdot ({x}-2)>0\).
Области допустимых значений (ОДЗ) здесь писать не надо, поскольку деления на переменную нет, и радикалов (корней) здесь не наблюдается.
На множители здесь все и так разложено за нас. Но не расслабляйся, это все, чтоб напомнить азы и понять суть!
Допустим, ты не знаешь метода интервалов, как бы ты стал решать это неравенство? Подойди логически и опирайся на то, что уже знаешь.
Во-первых, левая часть будет больше нуля если оба выражения в скобках либо больше нуля, либо меньше нуля, т.к. «плюс» на «плюс» дает «плюс» и «минус» на «минус» дает «плюс», так?
А если знаки у выражений в скобках разные, то в итоге левая часть будет меньше нуля.
А что же нам нужно, чтоб узнать те значения \( x\), при которых выражения в скобках будут отрицательными или положительными?
Нам нужно решить уравнение, оно точно такое же как неравенство, только вместо знака «\( >\)» будет знак «\(=\)«.
Корни этого уравнения и позволят определить те пограничные значения, при отступлении \( x\) от которых множители \( (x+1)\) и \( ({x}-2)\) будут больше или меньше нуля!
\( (x+1)\cdot ({x}-2)=0\) \( \displaystyle \left[ \begin{array}{l}x=-1\\x=2\end{array} \right.\)А теперь сами интервалы.
Что такое интервал?
Это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя какими-то числами – концами интервала. Эти промежутки в голове представить не так просто, поэтому интервалы принято рисовать, сейчас научу.
Рисуем ось \( X\), на ней располагается весь числовой ряд от \( -\infty \) и до \( +\infty \). На ось наносятся точки, те самые так называемые нули функции, значения, при которых выражение равняется нулю.
Эти точки «выкалываются» что означает, что они не относятся к числу тех значений, при которых неравенство верно. В данном случае, они выкалываются, т.к. знак в неравенстве \( >\), а не \(\ge\), то есть строго больше, а не больше или равно.

Хочу сказать, что ноль отмечать не обязательно, он без кружочков тут, а так, для понимания и ориентации по оси.
Ладно, ось нарисовали, точки (точнее кружочки) поставили, дальше что, как мне это поможет в решении? – спросишь ты.
Теперь просто…
Возьми значение для икса из интервалов по порядку и подставь их в свое неравенство и смотри, какой знак будет в результате умножения.
Короче, просто берем \( -2\) например, подставляем его сюда \( (x+1)\cdot ({x}-2)\), получится \( 4\), а \( 4>0\).
Значит на всем промежутке (на всем интервале) от \( -\infty \) до \( -1\), из которого мы брали \( -2\), неравенство будет справедливо.
Иными словами если икс от \( -\infty \) до \( -1\), то неравенство верно.
То же самое делаем и с интервалом от \( -1\) до \( 2\), берем \( 0\) или \( 1\), например, подставляем в \( (x+1)\cdot ({x}-2)\), определяем знак, знак будет «минус». И так же делаем с последим, третьим интервалом от \( 2\) до \( +\infty \), где знак получится «плюс».
Такая куча текста вышла, а наглядности мало, правда?
Взгляни еще раз на неравенство \( (x+1)\cdot ({x}-2)>0\).
Теперь все на ту же ось наносим еще и знаки, которые получатся в результате. Ломаной линией в моем примере обозначаем положительные и отрицательные участки оси.

Смотри на неравенство – на рисунок, опять на неравенство – и снова на рисунок, что-нибудь понятно?
Постарайся теперь сказать на каких промежутках икса, неравенство будет верно.
Правильно, от \( -\infty \) до \( -1\) неравенство будет справедливо и от \( 2\) до \( +\infty \).
А на промежутке от \( -1\) до \( 2\) неравенство \( <\) нуля и нас этот промежуток мало интересует, ведь у нас в неравенстве знак \( >\) стоит.
Ну, раз ты с этим разобрался, то дело за малым – записать ответ!
В ответ пишем те промежутки, при которых левая часть больше нуля, \( x\in (-\infty ;-1)\cup (2;+\infty )\), что читается, как икс принадлежит промежутку от минус бесконечности до минус одного и от двух до плюс бесконечности.
Стоит пояснить, что круглые скобки означают, что значения, которыми ограничен интервал не являются решениями неравенства, то есть они не включены в ответ, а лишь говорят о том, что до \( -1\), например, но \( -1\) не есть решение.
Теперь пример, в котором тебе придется не только интервал рисовать.
Пример 1
\( ({{x}^{2}}-1)\cdot ({x}-3)<0\)
Как думаешь, что надо сделать, прежде, чем точки на ось наносить? Ага, на множители разложить:
\( ({x}-1)\cdot (x+1)\cdot ({x}-3)<0\)
Рисуем интервалы и расставляем знаки, заметь точки у нас выколотые, потому, что знак строго меньше нуля:

Пришло время раскрыть тебе один секрет, который я обещал еще в начале этой темы!
Можно не подставлять значения из каждого интервала для определения знака, а определить знак в одном из интервалов, а в остальных просто чередовать знаки!
Таким образом, мы сэкономили немного времени на проставлении знаков – думаю, это выигранное время на ЕГЭ не помешает!
Пишем ответ:
\( x\in (-\infty \ ;-1)\cup (1\ ;3)\).
Пример №2
Теперь рассмотрим пример дробно-рационального неравенства – неравенство, обе части которого являются рациональными выражениями (см. «Рациональные уравнения»).
\( \frac{({x}-1)\cdot ({{x}^{2}}+2)}{{x}-4}\ge 0\)Что можешь сказать про это неравенство? А ты взгляни на него как на дробно-рациональное уравнение, что делаем в первую очередь?
Сразу видим, что корней нет, значит точно рациональное, но тут же дробь, да еще и с неизвестным в знаменателе!
Верно, ОДЗ надо!
Пример №3
\( \frac{1}{{{x}^{2}}-3x+2}\le \frac{1}{{x}-2}\)Раскладываем на множители и переносим все в одну сторону, нам ведь справа только ноль надо оставить, чтоб с ним сравнивать:
\( \displaystyle \begin{array}{l}\frac{1}{({x}-1)\cdot ({x}-2)}\le \frac{1}{{x}-2}\\\frac{1}{({x}-1)\cdot ({x}-2)}-\frac{1}{{x}-2}\le 0\\\frac{1-x+1}{({x}-1)\cdot ({x}-2)}\le 0\\\frac{-x+2}{({x}-1)\cdot ({x}-2)}\le 0\\\frac{{x}-2}{({x}-1)\cdot ({x}-2)}\ge 0\end{array}\)Обращаю твое внимание, что в последнем преобразовании, дабы получить в числителе \( \displaystyle {x}-2\) как и в знаменателе, умножаю обе части неравенства на \( -1\).
Помни, что при умножении обеих частей неравенства на \( -1\), знак неравенства меняется на противоположный!!!
Пишем ОДЗ:
\( \left\{ \begin{array}{l}x\ne 1\\x\ne 2\end{array} \right.\), иначе знаменатель обратится в ноль, а на ноль, как ты помнишь, делить нельзя!
Согласись, в получившемся неравенства так и подмывает сократить \( {x}-2\) в числителе и знаменателе! Этого делать нельзя, можно потерять часть решений или ОДЗ!
Теперь попробуй сам нанести точки на ось.
Замечу лишь, что при нанесении точек надо обратить внимание на то, что точка со значением \( 2\), которая исходя из знака \( \ge \), казалось бы, должна быть нанесена на ось как закрашенная, закрашенной не будет, она будет выколота!
Почему спросишь ты? А ты ОДЗ вспомни, не собираешься же ты на ноль делить так?
Запомни, ОДЗ превыше всего! Если все неравенство и знаки равенства говорят одно, а ОДЗ – другое, доверяй ОДЗ, великой и могучей!
Ну что, ты построил интервалы, я уверен, что ты воспользовался моей подсказкой по поводу чередования и у тебя получилось вот так (см. рисунок ниже) А теперь зачеркни, и не повторяй эту ошибку больше!
Какую ошибку? – спросишь ты.

Скажу так же, что бывают ситуации, когда есть корни неравенства, которые не входят в какой-либо промежуток, в ответ они записываются в фигурных скобках, вот так, например: \( \left\{ — \right.\left. 5 \right\}\).
Подробнее о таких ситуациях мы еще поговорим. А пока давай подведем итоги…
Алгоритм решения неравенств методом интервала
- Переносим все в левую часть, справа оставляем только ноль;
- Находим ОДЗ;
- Наносим на ось все корни неравенства;
- Берем произвольный ???? из одного из промежутков и определяем знак в интервале, к которому относится корень, чередуем знаки, обращая внимание на корни, повторяющиеся в неравенстве несколько раз, от четности или нечетности количества раз их повторения зависит, меняется знак при прохождении через них или нет;
- В ответ пишем интервалы, соблюдая выколотые и не выколотые точки (смотри ОДЗ), ставя необходимые виды скобок между ними.
Ну и наконец, наша любимая рубрика, «сделай сам»!
Примеры:
- \( \frac{{{x}^{2}}-10x+25}{{{x}^{2}}-3{x}-18}<0\);
- \( \frac{({{x}^{2}}-4x+4)\cdot ({{x}^{2}}-2x+1)}{{x}-1}\le 0\);
- \( \frac{{{({x}-1)}^{2}}\cdot (x+5)}{(x+2)\cdot x\cdot ({x}-3)\cdot {{({x}-4)}^{2}}}\ge 0\).
Ответы:
Метод интервалов для линейной функции
Линейной называется функция вида \( f\left( x \right)=ax+b\)
Рассмотрим для примера функцию \( f\left( x \right)={x}-3\).
Она положительна при \( x>3\) и отрицательна при \( x<3\). Точка \( x=3\) – нуль функции (\( f\left( 3 \right)=0\)).
Покажем знаки этой функции на числовой оси:
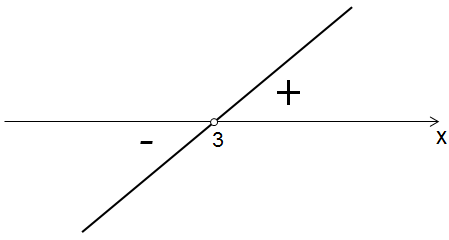
Говорим, что «функция меняет знак при переходе через точку \( x=3\)».
Видно, что знаки функции соответствуют положению графика функции: если график выше оси \( Ox\), знак «\( +\)», если ниже – «\( —\)».
Если обобщить полученное правило на произвольную линейную функцию, получим такой алгоритм:
- Находим нуль функции;
- Отмечаем его на числовой оси;
- Определяем знак функции по разные стороны от нуля.
Метод интервалов для квадратичной функции
Надеюсь, ты помнишь, как решаются квадратные неравенства? Если нет, прочти тему «Квадратные неравенства».
Напомню общий вид квадратичной функции: \( f\left( x \right)=a{{x}^{2}}+bx+c\).
Теперь вспомним, какие знаки принимает квадратичная функция.
Ее график – парабола, и функция принимает знак «\( +\)» при таких \( x\), при которых парабола выше оси \( Ox\), и «\( —\)» – если парабола ниже оси \( Ox\):
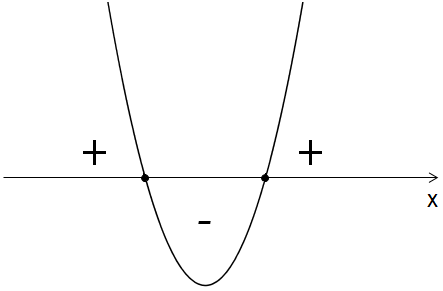
Если у функции есть нули (значения \( x\), при которых \( f\left( x \right)=0\)), парабола пересекает ось \( Ox\) в двух точках – корнях соответствующего квадратного уравнения.
Таким образом ось разбивается на три интервала, а знаки функции попеременно меняются при переходе через каждый корень.
Пожалуйста, загляни, если забыл, в статью о том, как использовать графики функций для решения уравнений, неравенств и систем.
А можно ли как-нибудь определить знаки, не рисуя каждый раз параболу?
Вспомним, что квадратный трехчлен можно разложить на множители: \( a{{x}^{2}}+bx+c=a\left( {x}-{{x}_{1}} \right)\left( {x}-{{x}_{2}} \right)\)
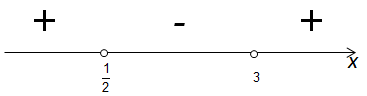
Например: \( 2{{x}^{2}}-7x+3=2\left( {x}-\frac{1}{2} \right)\left( {x}-3 \right)\).
Отметим корни на оси:

Мы помним, что знак функции может меняться только при переходе через корень.
Используем этот факт: для каждого из трех интервалов, на которые ось разбивается корнями, достаточно определить знак функции только в одной произвольно выбранной точке: в остальных точках интервала знак будет таким же.
В нашем примере: при \( x>3\) оба выражения в скобках положительны (подставим, например \( x=4\): \( 2\left( 4-\frac{1}{2} \right)\left( 4-3 \right)>0\)).
Ставим на оси знак «\( +\)»:
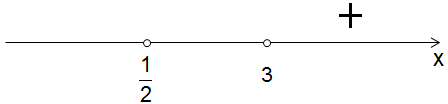
Далее, \( \frac{1}{2}<x<3\) (подставь в выражение \( 2\left( {x}-\frac{1}{2} \right)\left( {x}-3 \right)\) любой корень из этого интервала, например, \( x=2\)).
Первая скобка положительна, а вторая отрицательна. Значит, все произведение отрицательно: ставим на оси знак «\( —\)»:
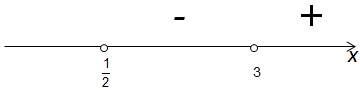
Ну и, при \( x<\frac{1}{2}\) (подставь, например, \( x=0\)) обе скобки отрицательны, значит, произведение положительно:
Случай, когда нулей у функции нет, или он всего один
Если их нет, то и корней нет. А значит, не будет и «перехода через корень». А значит, функция на всей числовой оси принимает только один знак.
Его легко определить, подставив в функцию \( x=0\).
Если корень только один, парабола касается оси \( Ox\), поэтому знак функции не меняется при переходе через корень. Какое правило придумаем для таких ситуаций?
Если разложить такую функцию на множители, получатся два одинаковых множителя:
\( a{{x}^{2}}+bx+c=a\left( {x}-{{x}_{1}} \right)\left( {x}-{{x}_{1}} \right)=a{{\left( {x}-{{x}_{1}} \right)}^{2}}\)А любое выражение в квадрате неотрицательно!
Поэтому знак функции и не меняется. В таких случаях будем выделять корень, при переходе через который знак не меняется, обведя его квадратиком:

Такой корень будем называть кратным.
Метод интервалов в неравенствах
Теперь любое квадратное неравенство можно решать без рисования параболы!
Достаточно только расставить на оси знаки квадратичной функции, и выбрать интервалы в зависимости от знака неравенства. Например:
\( 3{{x}^{2}}-5{x}-8\ge 0\text{ }\Leftrightarrow \text{ }3\left( x+1 \right)\left( {x}-\frac{8}{3} \right)\ge 0\)Отмерим корни на оси и расставим знаки:
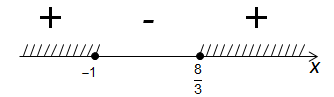
Нам нужна часть оси со знаком «\( +\)»; так как неравенство нестрогое, сами корни тоже включаются в решение:
\( x\in \left( -\infty ;-1 \right]\cup \left[ \frac{8}{3};+\infty \right)\).
Теперь рассмотрим рациональное неравенство – неравенство, обе части которого являются рациональными выражениями (см. «Рациональные уравнения»).
Рациональное неравенство
Пример 4
\( \frac{\left( {x}-2 \right)\left( x+3 \right)\left( {{x}^{2}}+1 \right)}{x\cdot \left( {x}-3 \right)}\ge 0\).
Все множители кроме одного – \( \left( {{x}^{2}}+1 \right)\) – здесь линейные, то есть, содержат переменную только в первой степени.
Такие линейные множители нам и нужны для применения метода интервалов – знак при переходе через их корни меняется.
А вот множитель \( \left( {{x}^{2}}+1 \right)\) вообще не имеет корней. Это значит, что он всегда положительный (проверь это сам), и поэтому не влияет на знак всего неравенства.
Значит, на него можно поделить левую и правую часть неравенства, и таким образом избавиться от него:
Пример 5: \( \frac{1}{{x}-3}\ge \frac{1}{{{x}^{2}}-5x+6}\).
Для применения метода интервалов нужно, чтобы в одной из частей неравенства был \( 0\). Поэтому перенесем правую часть налево:
\( \frac{1}{{x}-3}-\frac{1}{{{x}^{2}}-5x+6}\ge 0\).
Далее, в левой части нам необходимо получить произведение (желательно, линейных) множителей. Для этого приведем выражение к общему знаменателю и разложим его на такие множители:
Пример 6
И еще один очень показательный пример:
\( \frac{\left( {x}-1 \right)\left( x+3 \right){{\left( {x}-3 \right)}^{2}}{{\left( x+2 \right)}^{4}}}{\left( {x}-2 \right){{\left( x+3 \right)}^{2}}}\le 0\)Опять же, мы не сокращаем одинаковые множители числителя и знаменателя, так как, если сократим, нам придется специально запоминать, что нужно выколоть точку \( x=-3\).
Дальше, мы видим несколько кратных корней:
- \( x=3\): повторяется \( 2\) раза;
- \( x=-2\): \( 4\) раза;
- \( x=-3\): \( 3\) раза (\( 2\) в числителе и один в знаменателе).
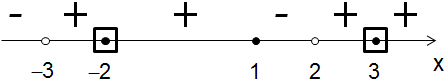
В случае четного количества поступаем так же, как и раньше: обводим точку квадратиком и не меняем знак при переходе через корень.
А вот в случае нечетного количества это правило не выполняется: знак все равно поменяется при переходе через корень. Поэтому с таким корнем ничего дополнительно не делаем, как будто он у нас не кратный.
Вышеописанные правила относятся ко всем четным и нечетным степеням.
Что запишем в ответе?
Примеры для самостоятельной работы
- \( \frac{\left( {{x}^{2}}-1 \right)\left( x+2 \right)}{\left( {x}-2 \right)}>0\)
- \( \frac{\left( {{x}^{2}}-2x+1 \right){{\left( x+1 \right)}^{3}}\left( {{x}^{2}}-1 \right)}{x\left( x+2 \right)}\le 0\)
Решения:
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Метод интервалов при решении рациональных и иррациональных уравнений и неравенств
В этом видео мы узнаем (вспомним) метод интервалов, поймём как и почему он работает.
Вспомним, как решать квадратные, рациональные неравенства, а также неравенства с модулем и иррациональные.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Здравствуйте, очень доступный и хороший материал. Жаль, что не рассматриваются неравенства с модулем. Спасибо
Здравствуйте, Лязят. Спасибо за теплые слова. У нас есть тема «Уравнения с модулем» Разберитесь с ней, пожалуйста. Неравенства решаются аналогично. Или же эта тема подробно разбирается на нашем платном тарифе «Репетитор«. Там вообще все очень подробно разбираем. Все темы ОГЭ и ЕГЭ. Еще подробнее, чем в этом учебнике.
Некоторые комментарии прошлых лет к этой статье:
Муниса
09 марта 2019
Спасибо огромное, очень помогли 🙂
ответить
Александр (админ)
09 марта 2019
Очень рады, Муниса. И тебе спасибо за найденные ошибки по другой теме )