Трапеция — определение, формулы и свойства
Перед тобой лучший гид по трапеции! Только то, что нужно. Без воды.
Основные определения, формулы и свойства.
Помни о своей цели!
Тебе нужно подготовиться к ЕГЭ по математике так, чтобы поступить в ВУЗ мечты!
Приступим?
Трапеция — коротко о главном
Что такое трапеция:
Трапеция – четырёхугольник, у которого две стороны параллельны (они называются основания), а две другие – нет (это боковые стороны).
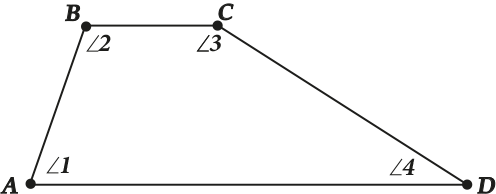
Сумма углов при каждой боковой стороне трапеции равна 180°
\( \displaystyle \angle 1+\angle 2=180{}^\circ \) и \( \displaystyle \angle 3+\angle 4=180{}^\circ \)
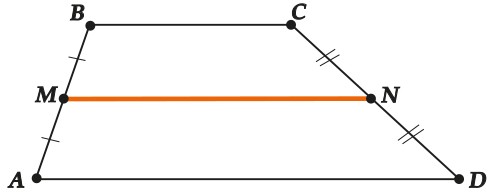
Средняя линия трапеции:
Средняя линия трапеции (\( \displaystyle MN\)) – отрезок, соединяющий середины боковых сторон: \( \displaystyle AM=MB,\ \ CN=ND\).
Средняя линия параллельна основаниям: \( \displaystyle MN\parallel BC\parallel AD\).
Длина средней линии трапеции равна полусумме длин оснований: \( \displaystyle MN=\frac{BC+AD}{2}\).
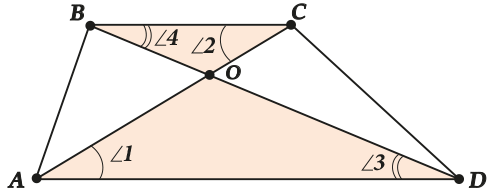
Диагонали трапеции:
Диагонали любой трапеции пересекаются в точке О.
Треугольники, образованные основаниями трапеции и отрезками диагоналей
(\( \displaystyle BOC\) и \( \displaystyle AOD\)) подобны по двум углам с коэффициентом подобия равным отношению оснований: \( \displaystyle k=\frac{BC}{AD}\).
Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны: \( \displaystyle {{S}_{\Delta AOB}}={{S}_{\Delta COD}}\).
Равнобедренная (равнобокая трапеция)
Равнобедренная (равнобокая) трапеция – это трапеция, у которой боковые стороны равны: \( \displaystyle AB=CD\).
Свойства равнобедренной трапеции:
Диагонали равны: \( \displaystyle AC=BD\);
Углы при основании равны: \( \displaystyle \angle A=\angle D,\text{ }\angle B=\angle C\);
Сумма противолежащих углов равна \( \displaystyle 180{}^\circ \): \( \displaystyle \angle A+\angle C=\angle B+\angle D=180{}^\circ \).
Стороны и диагональ равнобокой трапеции связаны соотношением: \( \displaystyle A{{C}^{2}}=B{{D}^{2}}=AD\cdot BC+A{{B}^{2}}\).

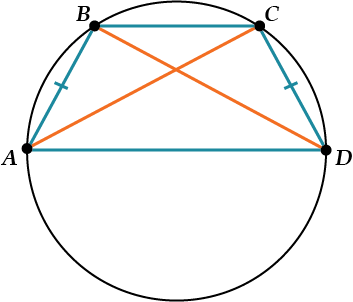
Если трапецию можно вписать в окружность…
Если трапецию можно вписать в окружность, то она – равнобокая.
Площадь трапеции
Площадь трапеции равна полусумме оснований, умноженной на высоту: \( \displaystyle {{S}_{ABCD}}=\frac{BC+AD}{2}\cdot h\).
Для справки: В нашем учебнике для подготовки к ЕГЭ по математике есть все темы планиметрии и стереометрии (да и алгебры тоже есть).
Что такое трапеция?
Трапеция – такой четырехугольник, у которого две стороны параллельны, а две другие – нет.
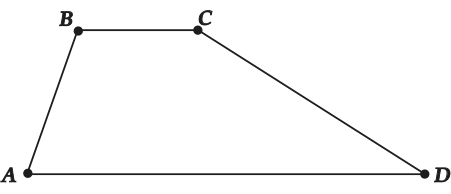
Параллельные стороны называются – основания, а непараллельные стороны называются боковые стороны.
Вот, смотри:
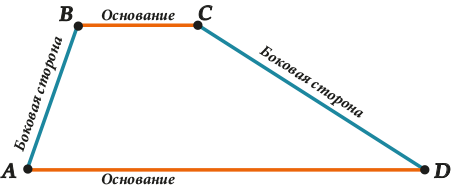
Оказывается, трапеция (как и треугольник) бывает равнобедренная.
Если боковые стороны трапеции равны, то она называется равнобедренной (или равнобокой).
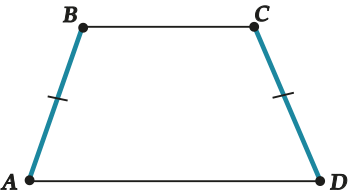
И тут возникает вопрос: а могут ли у трапеции быть равными ОСНОВАНИЯ?
А вот и нет. Тогда это получится не трапеция, а параллелограмм, потому что две стороны окажутся параллельны и равны (вспоминаем признаки параллелограмма)
Свойства трапеции
Итак, что ты должен знать о свойствах трапеции…
Сумма углов при каждой боковой стороне трапеции равна 180°. (у нас на рисунке \( \displaystyle \angle 1+\angle 2=180{}^\circ \) и \( \displaystyle \angle 3+\angle 4=180{}^\circ \))
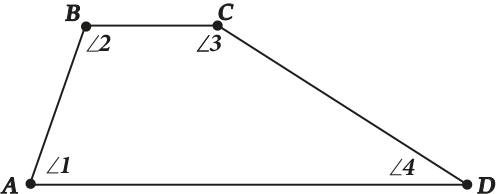
Почему так?
Ну, конечно, просто потому, что основания – параллельны, а боковая сторона – секущая.
Вот и получается, что \( \displaystyle \angle 1\) и \( \displaystyle \angle 2\) – внутренние односторонние углы при параллельных \( \displaystyle AD\) и \( \displaystyle BC\) и секущей \( \displaystyle AB\).
Поэтому \( \displaystyle \angle 1+\angle 2=180{}^\circ \).
И точно так же \( \displaystyle \angle 3\) и \( \displaystyle \angle 4\) – внутренние односторонние углы при тех же параллельных \( \displaystyle AD\) и \( \displaystyle BC\), но секущая теперь – \( \displaystyle CD\).
Видишь: главное, что играет роль – это параллельность оснований. Давай разберем еще некоторые свойства трапеции.
Как у всякого четырехугольника, у трапеции есть диагонали. Их две – посмотри на рисунки:
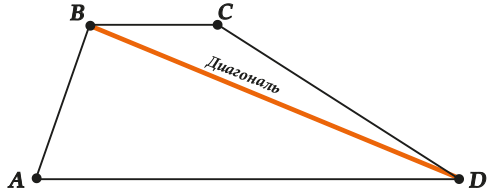
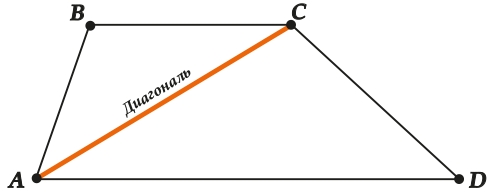
Снова порассуждаем об углах:
Опять \( \displaystyle AD\) и \( \displaystyle BC\) – параллельные, а диагональ \( \displaystyle AC\) – секущая. Поэтому \( \displaystyle \angle 1=\angle 2\).
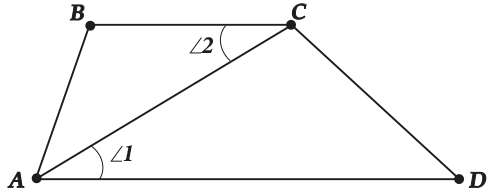
А теперь рассмотрим сразу 2 диагонали и 4 угла:
\( \displaystyle \angle 1=\angle 2\) \( \displaystyle \angle 3=\angle 4\)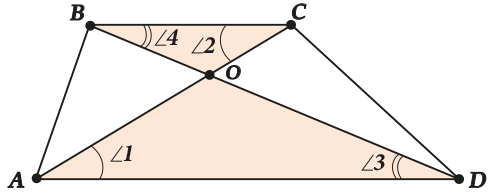
Что из этого может следовать?
Очень важный факт:
Треугольники \( \displaystyle BOC\) и \( \displaystyle AOD\) – подобны по двум углам.
Их коэффициент подобия равен отношению оснований: \( \displaystyle K=\frac{a}{b}\).
Средняя линия трапеции
Для начала – что же такое средняя линия трапеции?
Средняя линия трапеции –это отрезок, который соединяет середины боковых сторон трапеции.
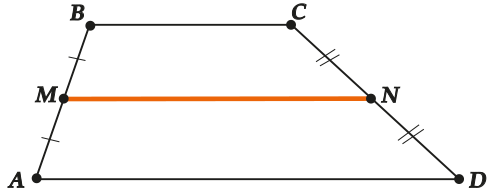
Оказывается, длину этой средней линии можно выразить через длины оснований трапеции. А именно, имеет место такая формула:
\( \displaystyle m=\frac{a+b}{2}\), то есть:
Длина средней линии трапеции равна полусумме (то есть половине суммы) длин оснований.
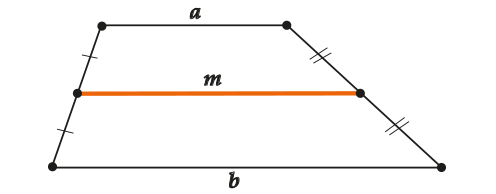
А еще…
Средняя линия трапеции параллельна ее основаниям.
Трапеция, вписанная в окружность
Даже если ты ещё не изучал темы «Окружность. Вписанный угол» и «Вписанный четырехугольник», тебе будет полезно (и, надеюсь, интересно) узнать следующий удивительный факт:
Если трапецию можно вписать в окружность, то она – равнобокая.
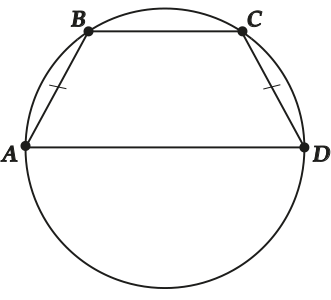
Доказывать это мы не будем (здесь, во всяком случае), а вот запомнить хорошо бы – пригодится!
Подведём итог – он короткий.
Самое важное, что есть в трапеции – две параллельные стороны и BCE свойства трапеции именно этим и определяются.
Так что, если у тебя в задаче трапеция, – используй параллельность и всё получится!
7 свойств трапеции
1-е свойство трапеции
Сумма углов при каждой боковой стороне трапеции равна 180°.
(у нас на рисунке \( \displaystyle \angle 1+\angle 2=180{}^\circ \) и \( \displaystyle \angle 3+\angle 4=180{}^\circ \))

Почему? \( \displaystyle AD\) и \( \displaystyle BC\) – параллельны, а \( \displaystyle AB\) и \( \displaystyle CD\) – секущие, поэтому:
- \( \angle 1+\angle 2=180{}^\circ \);
- \( \angle 3+\angle 4=180{}^\circ \).
2-е свойство трапеции
Треугольники \( \displaystyle BOC\) и \( \displaystyle AOD\) подобны по двум углам.
(\( \displaystyle \angle 1=\angle 2\) и \( \displaystyle \angle 3=\angle 4\) – как накрест лежащие)
3-е свойство трапеции
Сначала сформулируем основное определение, которое тебе нужно знать для понимания этого свойства трапеции:
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
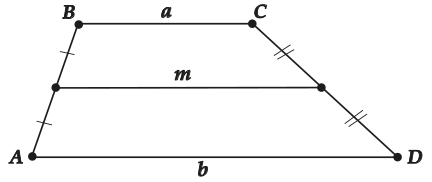
А теперь формула:
\( m=\frac{a+b}{2}\)А вот и само третье свойство трапеции:
Средняя линия трапеции равна полусумме оснований и параллельна им.
А это почему? Ту чуть – чуть сложнее – потребуется провести аж одну лишнюю линию!
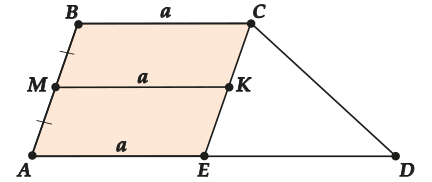
Итак, проведём \( \displaystyle CE\parallel AB\). Тогда четырехугольник \( \displaystyle ABCE\) – параллелограмм.
Возьмём середину \( \displaystyle M\) стороны \( \displaystyle AB\) и середину \( \displaystyle K\) стороны \( \displaystyle CE\).
Оба: \( \displaystyle MBCK\) и \( \displaystyle AMKE\) – снова параллелограммы (\( \displaystyle MB\parallel CK\) и \( \displaystyle MB=CK\); \( \displaystyle AM\parallel KE\) и \( \displaystyle AM=KE\)).
Ну вот, значит \( \displaystyle MK\parallel AD\), да ещё \( \displaystyle MK=BC=a\).
Поедем дальше.
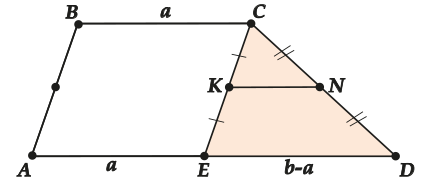
Проведём \( \displaystyle KN\) – среднюю линию в \( \displaystyle \Delta ECD\).
Знаем, что \( \displaystyle KN\parallel ED\) и \( KN=\frac{1}{2}ED\)
Что же из всего этого следует?
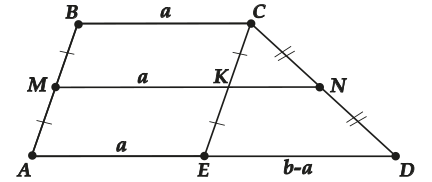
\( \displaystyle MN\parallel AD\) (так как через точку \( \displaystyle K\) можно провести лишь одну прямую параллельную \( \displaystyle AD\), поэтому \( \displaystyle MK\) и \( \displaystyle KN\) – одна прямая \( \displaystyle MN\))
\( \displaystyle MN=MK+KN=a+\frac{b-a}{2}\)
\( \displaystyle MN=\frac{a+b}{2}\)
Вот и доказали!
5-е свойство трапеции
В любой трапеции следующие четыре точки лежат на одной прямой:
- \( \displaystyle F\) и \( \displaystyle H\) – середины оснований
- \( \displaystyle E\) – точка пересечения продолжений боковых сторон;
- \( \displaystyle G\) – точка пересечения диагоналей.
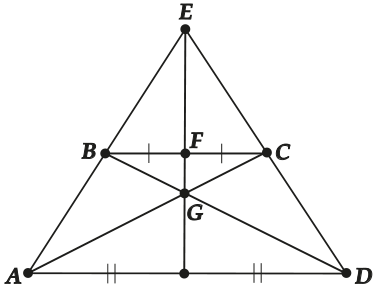
Эту теорему доказывать не будем – не пугайся. Заметим только, что ВЕРНО и ОБРАТНОЕ:
Если в каком-нибудь четырехугольнике какие-нибудь три из перечисленных четырёх точек окажутся на одной прямой, то четырёхугольник этот – ТРАПЕЦИЯ.
7-е свойство трапеции
Здесь мы ещё раз увидим, как полезно в трапеции бывает провести линию, параллельную или боковой стороне, или диагонали – сразу появляется новый взгляд.
Один раз мы уже так делали – в пункте про среднюю линию. А теперь ты узнал новый факт, который относительно часто встречается в задачах.
В трапеции с перпендикулярными диагоналями \( FH=\frac{AD+BC}{2}\)
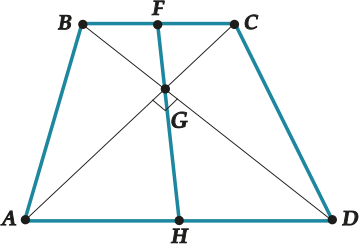
Давай докажем! Это уже целая задача, которая вполне может попасться прямо на ЕГЭ!
Ну вот, и ты теперь старайся с помощью новых знаний и методов решать задачки про трапецию – они обычно не слишком сложные.
Главное, твёрдо помнить все свойства трапеции и не забывать о параллельности оснований и иногда (в задачах посложнее) бывает полезно провести что-то параллельное или соединить боковые стороны.
Доказательство седьмого свойства трапеции
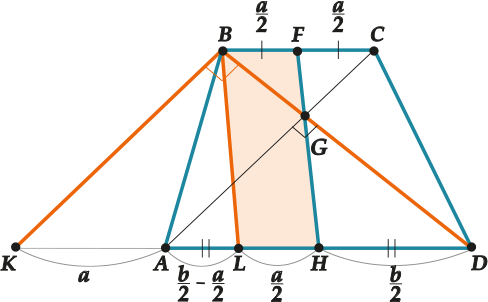
Проведём \( \displaystyle BK\parallel AC\) и \( \displaystyle BL\parallel FH\).
Обозначим \( \displaystyle BC=\text{ }a\); \( \displaystyle AD=b\).
Тогда:
- \( \displaystyle \Delta KBD\) – прямоугольный
- \( \begin{array}{l}\left\{ \begin{array}{l}LD=\frac{b}{2}+\frac{a}{2}=\frac{a+b}{2}\\LK=a+\frac{b}{2}-\frac{a}{2}=\frac{a+b}{2}\end{array} \right.\Rightarrow BL-медиана~в~\ \Delta KBD.\\\end{array}\)
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



А у меня задачка от 18 февраля 2020 года решилась.
Отлично, Александра!
Некоторые комментарии прошлых лет к этой статье:
никита
26 сентября 2018
вау помогло все так кратко и понятно
Дмитрий
18 декабря 2019
Очень помогает
Нурдана
18 февраля 2020
Определить площадь трапеции, если ее основания равны 6см и 11см, одна из боковых сторон 4см, а сумма углов при нижнем основании равна 90*. Олимпиадная задача
Алексей Шевчук
19 февраля 2020
Нурдана, в условии недостаточно данных. Сравни площади для случаев, если углы при основании равны 45 каждый и, например, если они 60 и 30 — площадь получится разная.