Квадратные неравенства
Чтобы разобраться, как решать квадратные неравенства, нам потребуется разобраться, что же такое квадратичная функция.
Зачем вообще нужна квадратичная функция? Какой у нее график? Где он применим?
Замечал, как летит брошенный мяч, по какой траектории движется струя в фонтане? А как думаешь как летит пуля?
По дуге? Самым верным ответом будет «по параболе»!
Парабола и есть график квадратичной функции.
Да стоит только оглядеться, и ты заметишь, что с параболой ты сталкиваешься ежедневно!
Таким образом, зная свойства квадратичной функции, можно будет решать многие практические задачи.
К примеру, под каким углом необходимо кинуть мяч, чтобы обеспечить наибольшую дальность полёта? Или, где окажется снаряд, если запустить его под определённым углом?
Итак, давай разбираться.
Квадратные неравенства — коротко о главном
Квадратичная функция–это функция вида: \( \displaystyle f\left( x \right)=a{{x}^{2}}+bx+c=0\), \( \displaystyle a\ne 0\)
График квадратичной функции – парабола. Её ветви направлены вверх, если \( \displaystyle a>0\), и вниз, если \( \displaystyle a<0\):
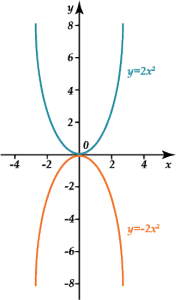
Если требуется найти числовой промежуток, на котором квадратный трёхчлен больше нуля, то это числовой промежуток, где парабола лежит выше оси \( Ox\).
Если требуется найти числовой промежуток, на котором квадратный трёхчлен меньше нуля, то это числовой промежуток, где парабола лежит ниже оси \( Ox\).
Виды квадратных неравенств
Все квадратные неравенства сводятся к следующим четырём видам:
\( \displaystyle \left. \begin{array}{l}a{{x}^{2}}+bx+c\ \ge 0\\a{{x}^{2}}+bx+c>0\\a{{x}^{2}}+bx+c\le 0\\a{{x}^{2}}+bx+c<0\end{array} \right\rangle a\ne 0\)Алгоритм решения квадратных неравенств:
1) Запишем соответствующее неравенству квадратное уравнение (просто меняем знак неравенства \( >,\text{ }<,\text{ }\ge ,\text{ }\le \) на знак равенства «\( \displaystyle=\)»).
Пример:
\( 2{{x}^{2}}+x-3\ge 0\)2) Найдём корни этого уравнения:
\( {{x}_{1}}=-\frac{3}{2};\text{ }{{x}_{2}}=1\)3) Отметим корни на оси \( Ox\) и схематично покажем ориентацию ветвей параболы («вверх» или «вниз»)
4) Расставим на оси знаки, соответствующие знаку квадратичной функции: там где парабола выше оси, ставим «\( +\)», а там где ниже – «\( —\)».
5) Выписываем интервал(ы), соответствующий(ие) «\( +\)» или «\( —\)», в зависимости от знака неравенства. Если неравенство нестрогое, корни входят в интервал, если строгое — не входят.
\( x\in \left( -\infty ;-\frac{3}{2} \right]\cup \left[ 1;+\infty \right)\)Квадратичная функция
Итак, давай разбираться.
Квадратичная функция – это функция, которую можно записать вот такой формулой: \( y=a{{x}^{2}}+bx+c\), где \( x\) – независимая переменная, \( a\), \( b\) и \( c\) – некоторые числа, при этом \( a\ne 0\).
К примеру, \( y=2{{x}^{2}}-3x+4\). Чему здесь равны \( a\), \( b\) и \( c\)?
Ну, конечно, \( a=2\), \( b=-3\) и \( c=4\)!
Как уже упоминалось в теме «Квадратные уравнения», графиком такой функции выступает парабола.
В зависимости от значения \( a\) ветви графика направлены вверх или вниз:
- если \( a>0\), то ветви параболы направлены вверх;
- если \( a<0\), то ветви параболы направлены вниз.
Для того, чтобы легко это запомнить, обратимся к хорошо известным тебе смайликам:
- Если \( a>0\), т.е. a – положительное число, раз положительное, значит все хорошо – улыбаемся! А ветви графика тем временем направлены вверх 🙂
- Если \( a<0\), т.е. a – отрицательное число, а раз отрицательное, значит, есть повод взгрустнуть, а ветви графика тем временем будут направлены вниз 🙁
При этом точки пересечения параболы с осью \( x\), называются нулями функции и являются корнями соответствующего квадратного уравнения:
\( y=a{{x}^{2}}+bx+c=0\)А теперь еще раз тоже самое но более сжато (то есть на языке математики)
Прежде чем говорить о теме «квадратные неравенства», вспомним что такое квадратичная функция и что из себя представляет её график.
Квадратичная функция – это функция вида \( f\left( x \right)=a{{x}^{2}}+bx+c=0\), \( a\ne 0\)
Другими словами, это многочлен второй степени.
График квадратичной функции – парабола (помнишь, что это такое?)
- если \( a>0\), то ветви параболы направлены вверх;
- если \( a<0\), то ветви параболы направлены вниз.
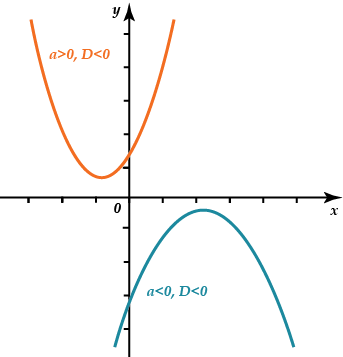
Если парабола не пересекает ось Х и ее ветви направлены вверх, функция при всех значениях Х принимает лишь положительные значения.
Если парабола не пересекает ось Х и ее ветви направлены вниз – лишь отрицательные.
В случае, когда у уравнения (\( 1\)) ровно один корень (например, если дискриминант равен нулю), это значит, что график касается оси \( Ox\):

Тогда, аналогично предыдущему случаю, при \( a>0\) функция неотрицательна \( \left( f(x) \ge 0 \right)\) при всех \( x\), а при \( a<0\) – неположительна \( \left( f(x) \le 0 \right)\).
Так вот, мы ведь недавно уже научились определять, где квадратичная функция больше нуля, а где – меньше:
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток, если строгое — не входят.
Если корень только один, – ничего страшного, будет везде один и тот же знак. Если корней нет, всё зависит только от коэффициента \( a\): если \( a>0\), то всё выражение больше 0, и наоборот.
Ну что, уловил? Тогда давай смотреть примеры!
Пример 1
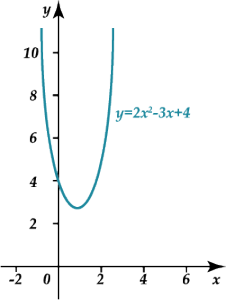
На рисунке выше изображён график функции \( y=2{{x}^{2}}-3x+4\).
Как мы уже отмечали, \( a=2\), а это больше нуля (улыбаемся), поэтому ветви графика направлены вверх.
Кроме того, можно заметить, что данный график не пересекает ось \( x\). Помнишь, что в таком случае происходит, если решать уравнение \( 2{{x}^{2}}-3x+4=0\)?
Все верно, корней такое уравнение иметь не будет, так как y принимает только положительные значения (не принимает значения, равные \( 0\))!
Если забыл, то вперёд повторять «Квадратные уравнения»!
А что, если \( a=-2\), т.е. меньше нуля? Ну конечно, мы «грустим», а, значит, ветви будут направлены вниз! Давай посмотрим на графике.
Пример 2
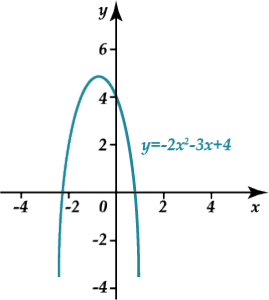
На этом рисунке изображён график функции \( y=-2{{x}^{2}}-3x+4\).
Так как \( a=-2\), т.е. меньше нуля, ветви параболы направлены вниз.
Кроме того, ты, наверное, уже заметил, что ветви этой параболы пересекают ось \( x\), а значит, уравнение \( -2{{x}^{2}}-3x+4=0\) имеет 2 корня, а функция принимает как положительные и отрицательные значения!
В самом начале, когда мы давали определение квадратичной функции, было сказано, что \( b\) и \( c\) – некоторые числа.
А могут ли они быть равны нулю? Ну конечно, могут!
Даже открою еще больший секрет (который и не секрет вовсе, но упомянуть о нем стоит): на эти числа (\( b\) и \( c\)) вообще никакие ограничения не накладываются!
Ну что, давай посмотрим, что будет с графиками, если \( b\) и \( c\) равны нулю.
Пример 3

Как видно, графики рассматриваемых функций (\( y=2{{x}^{2}}\) и \( y=-2{{x}^{2}}\)) сместились так, что их вершины находятся теперь в точке с координатами \( \left( 0;0 \right)\)
То есть на пересечении осей \( x\) и \( y\), на направлении ветвей это никак не отразилось.
Таким образом, можно сделать вывод, что \( b\) и \( c\) отвечают за «передвижения» графика параболы по системе координат.
График функции \( y=2{{x}^{2}}\) касается оси \( x\) в точке \( \left( 0;0 \right)\). Значит, уравнение \( 2{{x}^{2}}=0\) имеет один корень.
Таким образом, функция принимает значения больше либо равные нулю.
Придерживаемся той же логики с графиком функции \( y=-2{{x}^{2}}\).
Он касается оси x в точке \( \left( 0;0 \right)\). Значит, уравнение \( -2{{x}^{2}}=0\) имеет один корень.
Таким образом, функция принимает значения меньше либо равные нулю, то есть \( y\le 0\).
Значит, чтобы определить знак выражения, первое, что необходимо сделать – это найти корни уравнения. Это нам очень пригодится.
Квадратные неравенства
Квадратное неравенство – это неравенство, состоящее из одной квадратичной функции. Таким образом, все квадратные неравенства сводятся к следующим четырём видам:
\( \left. \begin{array}{l}a{{x}^{2}}+bx+c\ge 0\\a{{x}^{2}}+bx+c>0\\a{{x}^{2}}+bx+c\le 0\\a{{x}^{2}}+bx+c<0\end{array} \right\rangle a\ne 0\)
При решении таких неравенств нам пригодятся умения определять, где квадратичная функция больше, меньше, либо равна нулю.
То есть:
- Если перед нами неравенство вида \( a{{x}^{2}}+bx+c>0\), то фактически задача сводится к тому, чтобы определить числовой промежуток значений \( x\), при котором парабола лежит выше оси \( x\).
- если перед нами неравенство вида \( a{{x}^{2}}+bx+c<0\), то фактически задача сводится к тому, чтобы определить числовой промежуток значений x, при котором парабола лежит ниже оси \( x\).
Если неравенства нестрогие (\( a{{x}^{2}}+bx+c\ \ge 0\) и \( a{{x}^{2}}+bx+c\le 0\)), то корни (координаты \( x\) пересечений параболы с осью \( x\)) включаются в искомый числовой промежуток, при строгих неравенствах – исключаются.
Это все достаточно формализовано, однако не надо отчаиваться и пугаться! Сейчас разберём примеры, и все станет на свои места.
При решении квадратных неравенств будем придерживаться приведённого алгоритма, и нас ждёт неизбежный успех!
Алгоритм решения квадратных неравенств
1) Запишем соответствующее неравенству квадратное уравнение (просто меняем знак неравенства \( >,\text{ }<,\text{ }\ge ,\text{ }\le \) на знак равенства «\( \displaystyle=\)»).
Пример:
\( 2{{x}^{2}}+x-3\ge 0\)2) Найдём корни этого уравнения:
\( {{x}_{1}}=-\frac{3}{2};\text{ }{{x}_{2}}=1\)3) Отметим корни на оси \( Ox\) и схематично покажем ориентацию ветвей параболы («вверх» или «вниз»)
4) Расставим на оси знаки, соответствующие знаку квадратичной функции: там где парабола выше оси, ставим «\( +\)», а там где ниже – «\( —\)».
5) Выписываем интервал(ы), соответствующий(ие) «\( +\)» или «\( —\)», в зависимости от знака неравенства. Если неравенство нестрогое, корни входят в интервал, если строгое — не входят.
\( x\in \left( -\infty ;-\frac{3}{2} \right]\cup \left[ 1;+\infty \right)\)Разобрался? Тогда вперёд закреплять!
11 решенных квадратных неравенств
Примеры 4 — 11
- \( 3{{x}^{2}}-4{x}-2\ge 0\)
- \( -3{{x}^{2}}-17x+6<0\)
- \( 4{{x}^{2}}+4x+1\le 0\)
- \( 4{{x}^{2}}+3x+18>0\)
- \( -3{{x}^{2}}+2x+5\le 0\)
- \( 25{{x}^{2}}-30x+9>0\)
- \( 2{{x}^{2}}+4x+3<0\)
- \( {{x}^{2}}\le 9\)
Ну что, получилось? Если возникли затруднения, то разбирайся в решениях.
Решение примера №4
\( 3{{x}^{2}}-4{x}-2\ge 0\)Запишем соответствующее квадратное уравнение:
\( 3{{x}^{2}}-4{x}-2=0\)Найдём корни данного квадратного уравнения:
\( D={{\left( -4 \right)}^{2}}-4\cdot 3\cdot \left( -2 \right)=40\)
\( {{x}_{1}}=\frac{-\left( -4 \right)+\sqrt{40}}{2\cdot 3}=\frac{4+2\sqrt{10}}{6}=\frac{2}{3}+\frac{1}{3}\sqrt{10}=\frac{1}{3}\left( 2+\sqrt{10} \right);\)
\( {{x}_{2}}=\frac{-\left( -4 \right)-\sqrt{40}}{2\cdot 3}=\frac{4-2\sqrt{10}}{6}=\frac{2}{3}-\frac{1}{3}\sqrt{10}=\frac{1}{3}\left( 2-\sqrt{10} \right)\)
Схематично отметим полученные корни на оси и расставим знаки:

Выпишем интервалы, соответствующие знаку «\( +\)», так как знак неравенства «\( \ge \)». Неравенство нестрогое, поэтому корни включаются в интервалы:
\( x\in \left( -\infty ;\frac{1}{3}\left( 2-\sqrt{10} \right) \right]\cup \left[ \frac{1}{3}\left( 2+\sqrt{10} \right);\infty \right)\)Решение примера №5
\( -3{{x}^{2}}-17x+6<0\)
Запишем соответствующее квадратное уравнение:
\( -3{{x}^{2}}-17x+6=0\)
Найдём корни данного квадратного уравнения:
\( D={{\left( -17 \right)}^{2}}-4\cdot 6\cdot \left( -3 \right)=289+72=361\)
\( {{x}_{1}}=\frac{-\left( -17 \right)+\sqrt{361}}{2\cdot \left( -3 \right)}=\frac{17+19}{-6}=-\frac{36}{6}=-6;\)
\( {{x}_{2}}=\frac{-\left( -17 \right)-\sqrt{361}}{2\cdot \left( -3 \right)}=\frac{17-19}{-6}=\frac{2}{6}=\frac{1}{3};\)
Схематично отметим полученные корни на оси и расставим знаки:
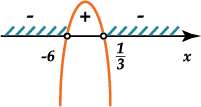
Выпишем интервалы, соответствующие знаку «\( —\)», так как знак неравенства «\( <\)». Неравенство строгое, поэтому корни не включаются в интервалы:
\( x\in \left( -\infty ;-6 \right)\cup \left( \frac{1}{3};\infty \right)\)Решение примера №6
\( 4{{x}^{2}}+4x+1\le 0\)Запишем соответствующее квадратное уравнение:
\( 4{{x}^{2}}+4x+1=0\)
Найдём корни данного квадратного уравнения:
\( D={{4}^{2}}-4\cdot 4\cdot 1=0\Rightarrow \)данное уравнение имеет один корень
\( x=\frac{-4\pm \sqrt{0}}{2\cdot 4}=\frac{-4}{8}=-\frac{1}{2}\)
Схематично отметим полученные корни на оси и расставим знаки:
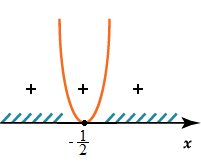
Выпишем интервалы, соответствующие знаку «\( —\)», так как знак неравенства «\( \le \)». При любом \( x\) функция \( y=4{{x}^{2}}+4+1\) принимает неотрицательные значения. Так как неравенство нестрогое, то ответом будет \( x=-\frac{1}{2}\).
Решение примера №7
\( 4{{x}^{2}}+3x+18>0\)
Запишем соответствующее квадратное уравнение:
\( 4{{x}^{2}}+3x+18=0\)
Найдём корни данного квадратного уравнения:
\( D={{3}^{2}}-4\cdot 4\cdot 18=9-288=-279\Rightarrow \) данное уравнение корней не имеет
Схематично нарисуем график параболы и расставим знаки:
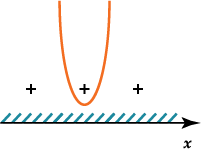
Выпишем интервалы, соответствующие знаку «\( +\)», так как знак неравенства «\( >\)». При любом \( x\) функция \( y=4{{x}^{2}}+3x+18\) принимает положительные значения, следовательно, решением неравенства будет интервал:
\( x\in \left( -\infty ;\infty \right)\)Решение примера №8
\( -3{{x}^{2}}+2x+5\le 0\) \( D=4-4\cdot \left( -3 \right)\cdot 5=64={{8}^{2}}\) \( {{x}_{1}}=\frac{-2+8}{-6}=-1;\text{ }{{x}_{2}}=\frac{-2-8}{-6}=\frac{5}{3}\)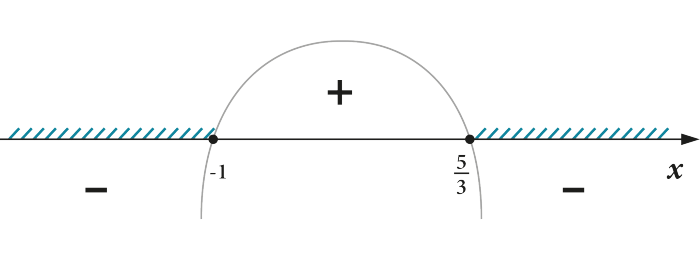
Решение примера №9
\( 25{{x}^{2}}-30x+9>0\) \( D={{\left(-30 \right)}^2}-4\cdot 25 \cdot 9 = 0\) \( {{x}_{1,2}}=\frac{30}{50}=\frac{3}{5}=0,6\)
Решение примера №10
\( 2{{x}^{2}}+4x+3<0\)
\( D={{4}^{2}}-4\cdot 2\cdot 3=-8<0\)
Корней нет, поэтому всё выражение в левой части принимает знак старшего коэффициента: \( 2>0 \Rightarrow 2{{x}^{2}}+4x+3>0\) при всех \( x\). А значит, решений неравенства нет.
Решение примера №11
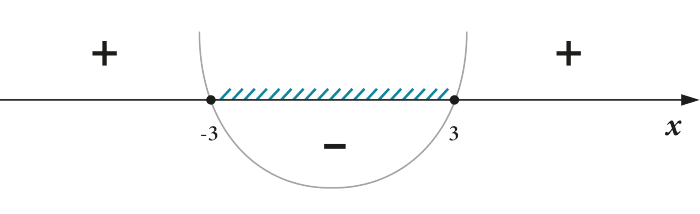
\( {{x}^{2}}\le 9\text{ }\Leftrightarrow \text{ }{{x}^{2}}-9\le 0\)Если квадратичная функция в левой части «неполная» – тем проще находить корни:
\( {{x}_{1}}=-3;\text{ }{{x}_{2}}=3\).
Бонус: Вебинары из нашего курса по подготовке к ЕГЭ по математике
Метод интервалов при решении рациональных и иррациональных уравнений и неравенств
В этом видео мы узнаем (вспомним) метод интервалов, поймём как и почему он работает.
Вспомним, как решать квадратные, рациональные неравенства, а также неравенства с модулем и иррациональные.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Александр
16 декабря 2019
Спасибо дружище, очень благодарен
Дарья
07 января 2020
Спасибо огромное за замечательный сайт!
Александр (админ)
07 января 2020
Дарья, и тебе спасибо. Очень приятно!