Квадратичная функция
Проверь себя, ответь на эти вопросы:
- Как выглядит квадратичная функция в общем виде (формула)?
- Как называется график квадратичной функции?
- Как влияет старший коэффициент на график квадратичной функции?
- Как построить график квадратичной функции?
- Какие есть варианты расположения графика?
В конце статьи ты будешь знать ответы на эти вопросы.
Поехали!
Квадратичная функция — коротко о главном
Квадратичная функция – функция вида \( y=a{{x}^{2}}+bx+c\), где \( a\ne 0\), \( b\) и \( c\) – любые числа (коэффициенты), \( c\) – свободный член.
График квадратичной функции – парабола.
Вершина параболы: \( \displaystyle {{x}_{в}}=\frac{-b}{2a}\).
Квадратичная функция вида: \( y=a{{x}^{2}}\).
Если коэффициент \( \displaystyle \mathbf{a}<\mathbf{0}\), ветви параболы направлены вниз, если \( \displaystyle \mathbf{a}>\mathbf{0}\) — ветви параболы направлены вверх.
Чем больше значение \( \displaystyle a\) (по модулю), тем у́же становится парабола (ветви становятся более крутыми). И наоборот, чем меньше \( \displaystyle a\), тем парабола шире.
Варианты расположения параболы в зависимости от коэффициента \( \displaystyle a\) и дискриминанта \( \displaystyle D={{b}^{2}}-4ac\).
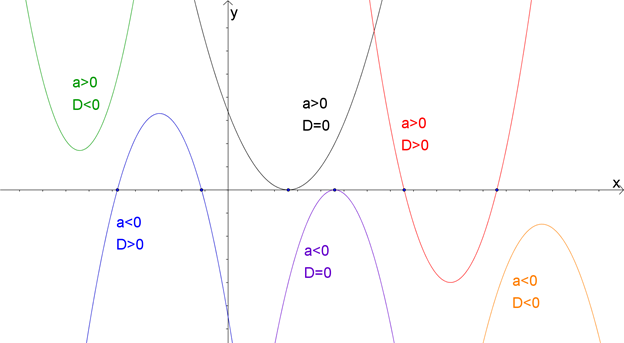
Алгоритм построения графика квадратичной функции — параболы:
- Найти координаты вершины;
- Построить ось симметрии, проанализировать куда направлены ветви параболы;
- Найти точки пересечения параболы с осью \( \displaystyle Ox\) (нули), если они есть, решив уравнение \( \displaystyle 0=a{{x}^{2}}+bx+c\);
- Найти точку пересечения с осью \( \displaystyle Oy\), решив уравнение \( \displaystyle y=a\cdot 0+b\cdot 0+c=c\).
Что такое функция?
Не знаешь? Тогда сперва прочитай тему «Функции» – она несложная, но очень важная.
А мы пока повторим.
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Что значит «допустимому»? Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции».
Все дело в понятии «область определения»:
Для некоторых функций не все аргументы можно подставить в зависимость.
Например, для функции \( y=\sqrt{x}\) отрицательные значения аргумента \( x\) – недопустимы.
Кстати, а с линейной функцией ты уже дружишь? Про нее все написано в теме «Линейная функция» – там ты поймешь, что в функциях ничего страшного нет и научишься понимать и использовать коэффициенты (это циферки перед буквой \( x\)).
И еще, надеюсь, ты умеешь решать квадратные уравнения? Освежить память можно, почитав тему «Квадратные уравнения».
Итак, приступим!
Квадратичная функция — подробнее
Квадратичная функция – это функция вида \( y=a{{x}^{2}}+bx+c\), где \( a\ne 0\), \( b\) и \( c\) – любые числа (они и называются коэффициентами).
Число \( a\) называют старшим или первым коэффициентом такой функции, \( b\) – вторым коэффициентом, а \( c\) – свободным членом.
Другими словами, квадратичная функция – это зависимость, содержащая аргумент в квадрате. Отсюда и ее название.
Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения \( D\left( y \right)\) и область значений\( E\left( y \right)\).
Какими могут быть значения аргумента квадратичной функции \( y=a{{x}^{2}}+bx+c\)? Правильно, любыми. Ведь в эту формулу можно подставить любое число (в отличии, например, от функции \( y=\frac{1}{x}\) – в нее нельзя подставить \( x=0\)).
Значит, область определения – все действительные числа:
\( D\left( y \right)=\mathbb{R}\) или \( D\left( y \right)=\left( -\infty ;+\infty \right)\).
А теперь множество значений. Все ли значения может принимать функция?
Достаточно рассмотреть самую простую квадратичную функцию \( y={{x}^{2}}\) \( \left( a=1,\text{ }b=0,\text{ }c=0 \right)~\), чтобы убедиться в обратном: ведь какое бы число мы не возводили в квадрат, результат всегда будет больше или равен нулю.
Значит, эта функция всегда не меньше нуля.
А вот больше нуля она может быть сколько угодно: ведь бесконечно большой x в квадрате будет еще больше.
Таким образом, можем написать для \( y={{x}^{2}}:E\left( y \right)=\left[ 0;+\infty \right)\).
В каждом отдельном случае область значений будет разная, но всегда – ограниченная.
График квадратичной функции
Наверняка ты слышал, что график квадратичной функции называется параболой. Как она выглядит? Сейчас нарисуем
Кстати мы очень подробно разобрали как быстро и правильно рисовать параболу. Переходи по ссылке и всему научишься.
Начнем с простейшей квадратичной функции – \( y={{x}^{2}}\).
Составим таблицу значений:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 4 |
Нарисуем эти точки на координатной плоскости и соединим их плавной линией:

Именно так и выглядит парабола. Самая нижняя ее точка называется вершиной, а части спарва и слева от вершины называем ветвями параболы. Как видим, ветви симметричны относительно вертикали, проходящей через вершину.
Рассмотрим теперь другую функцию: \( y={{x}^{2}}-2{x}-3\).
Составим таблицу значений:
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 5 | 0 | -3 | -4 | -3 | 0 | 5 |

Сравним два рисунка.
Видно, что это как будто одна и та же парабола, просто расположенная в разных местах.
Во второй параболе вершина переместилась в точку \( \left( 1;-4 \right)\), а ветви переехали вместе с ней.
Да, так оно и есть: все параболы с одинаковым старшим коэффициентом, a выглядят одинаково – даже при разных остальных коэффициентах.
Кстати, если хочешь научиться быстро и правильно рисовать график квадратичной функции, то переходи по ссылке, там отличная статья.
Коэффициенты квадратичной функции
Давай разберем, на что влияют коэффициенты квадратичной функции.
Начнем со старшего коэффициента.
Будем рассматривать функции вида \( y=a{{x}^{2}}\) (\( b=0\), \( c=0\) – пусть не мешают).
Построим на одном рисунке графики нескольких функций: при \( a= -2,\text{ }-1,\frac{1}{2},\text{ }1,\text{ }3:\)
Что ты видишь? Чем они отличаются? Какую закономерность можно заметить?
Во-первых, это невозможно не заметить, если \( \displaystyle \mathbf{a}<\mathbf{0}\), ветви парабол направлены вниз, а если \( \displaystyle \mathbf{a}>\mathbf{0}\) – вверх.
Так, хорошо.
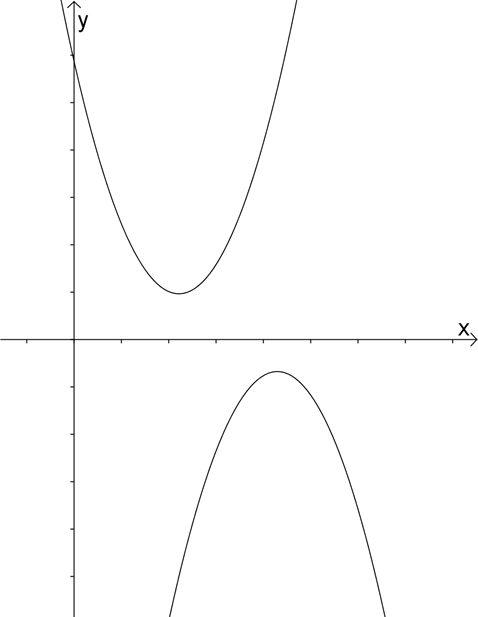
Значит, если парабола пересекает ось \( \displaystyle Ox\) в двух точках, то у нас два корня квадратного уравнения.
Если не пересекает – корней нет.
Но бывает ведь, что дискриминант уравнения равен нулю, и тогда только один корень. В этом случае парабола касается оси \( \displaystyle Ox\) вершиной:

А что такое вершина параболы?
Вершина параболы
Корень уравнения в этом случае указывает на вершину параболы. Если вспомнить формулу корня квадратного уравнения при \( \displaystyle D=0\), получим формулу вершины:
\( \displaystyle {{x}_{в}}=\frac{-b}{2a}\).
Это тоже бывает очень полезно.
Итак, всего возможны шесть разных вариантов расположения параболы. Вот они все на одном рисунке:

А теперь порешаем задачки.
Решение задач
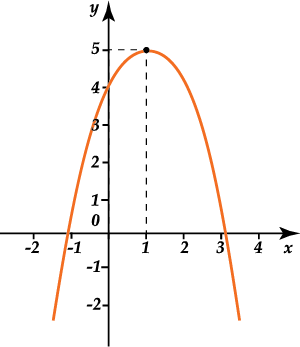
1. График какой из функций избражен на рисунке?
a) \( y=-{{x}^{2}}+2x+5\)
b) \( y={{x}^{2}}-2x+5\)
c) \( y=-{{x}^{2}}-2x+4\)
d) \( y=-{{x}^{2}}+2x+4\)
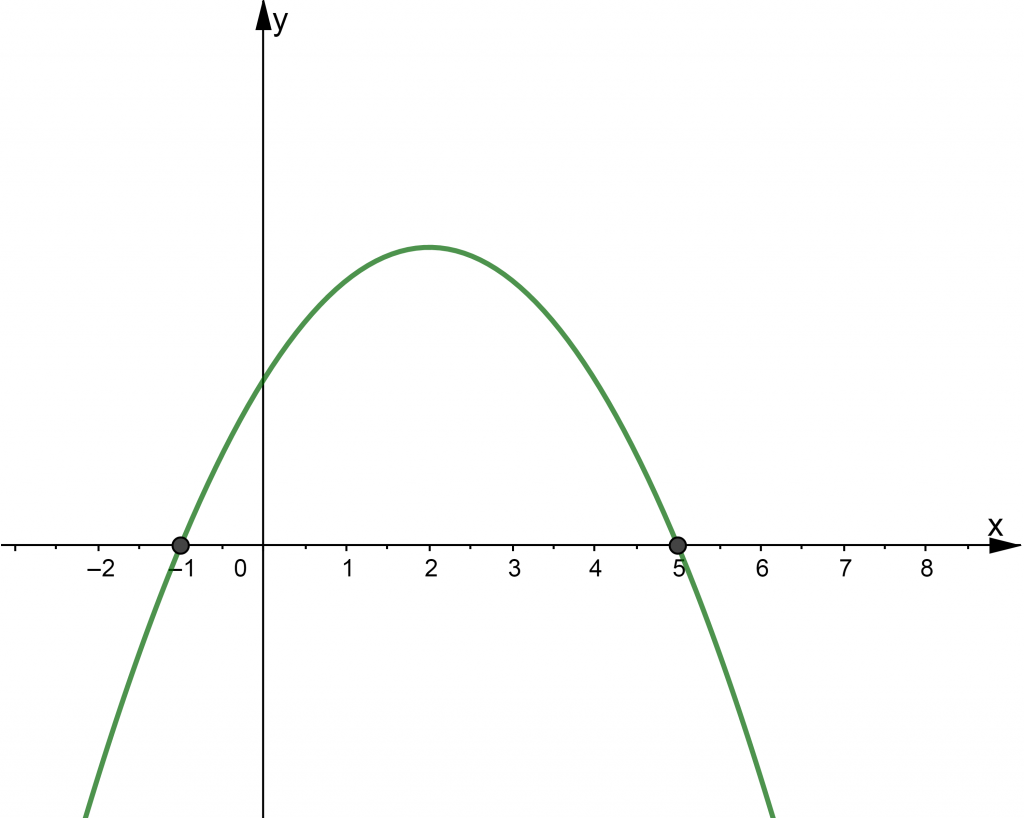
2. Найдите сумму корней квадратного уравнения \( a{{x}^{2}}+bx+c=0\), если на рисунке приведен график функции \( y=a{{x}^{2}}+bx+c\):

3. Найдите произведение корней квадратного уравнения \( a{{x}^{2}}+bx+c=0\), если на рисунке приведен график функции \( y=a{{x}^{2}}+bx+c\):
4. По графику функции \( y={{x}^{2}}+bx+c\) определите коэффициенты \( b\) и \( c\):

Решения
1. Первое: куда «смотрят» ветви параболы? Вниз. А что это значит? Правильно, \( \displaystyle a<0\). То есть вариант b) сразу не подходит.
Дальше посмотрим на точку пересечения с осью \( \displaystyle Oy:y=4\). Что нам дает эта точка? Вспоминай.
Это – свободный член c. Значит, \( \displaystyle c=4\) – отбросим вариант a).
Ну что же, \( \displaystyle a=-1,c=4,\) осталось определить b. Тут нам поможет вершина. Напоминаю, что ее координата вычисляется по формуле: \( \displaystyle {{x}_{в}}=\frac{-b}{2a}\).
В нашем случае \( \displaystyle {{x}_{в}}=1\). Тогда:
\( \displaystyle 1=\frac{-b}{2\cdot \left( -1 \right)}\text{ }\Rightarrow \text{ }b=2\).
Итак, наша парабола задается формулой: \( \displaystyle y=-{{x}^{2}}+2x+4\). Это вариант ответа d)
2. Проще простого: корни – это точки пересечения параболы с осью \( \displaystyle Ox\).
Смотрим: \( \displaystyle {{x}_{1}}=1\), \( \displaystyle {{x}_{2}}=5\). Значит, их сумма \( \displaystyle {{x}_{1}}+{{x}_{2}}=6\).
3. То же самое: \( \displaystyle {{x}_{1}}=-1\), \( \displaystyle {{x}_{2}}=5\). Произведение: \( \displaystyle {{x}_{1}}\cdot {{x}_{2}}=-5\).
4. Хм… Ну, коэффициент с мы бы нашли, да только по оси \( \displaystyle Oy\) нет обозначений. Зато показаны точки пересечения с осью \( \displaystyle Ox\). А это ведь корни уравнения \( \displaystyle {{x}^{2}}+bx+c=0:{{x}_{1}}=-1,{{x}_{2}}=4\).
Как это нам поможет?
Кстати, чему равен старший коэффициент?
Он равен \( \displaystyle 1\). Как называется такое квадратное уравнение? Вспоминай: оно называется приведенным. Теперь догадался? Можно ведь применить теорему Виета. Точно! Ведь она говорит нам, что сумма корней равна второму коэффициенту с обратным знаком:
\( \displaystyle {{x}_{1}}+{{x}_{2}}=-b\),
а произведение – свободному члену:
\( \displaystyle {{x}_{1}}\cdot {{x}_{2}}=c\).
Ну вот и решили: \( \displaystyle b=-\left( -1+4 \right)=-3\), \( \displaystyle c=-1\cdot 4=-4\).
Ответ: \( \displaystyle -3;\text{ -}4.\)
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)
Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.
Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики.
На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях).
Мы рассмотрим:
- степенную функцию (линейную, квадратичную, обратную зависимость, корни),
- тригонометрические и обратные тригонометрические,
- показательную и
- логарифмическую функции.
Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



3. То же самое: x1=−1, x2=3. Произведение: x1⋅x2=−3.
Простите, может я чего-то не понимаю или это просто опечатка, но на графике второй корень = 5. Или нет?
Дилнура, спасибо, там действительно 5, а не 3. Исправил
Спасибо. Зарегистрировалась. Поработала. Все доступно, понятно. Внука готовлю к ЕГЭ-22.
Удачи, Елена! Вам и вашему внуку. Почему-то у нас бабушки и дедушки, которые готовят внуков к ЕГЭ, встречаются чаще, чем родители)