Линейная функция
Зависимость одной величины от другой математики называют функций одной величины от другой.
Количество денег — это функция вашей зарплаты (иногда говорят «от зарплаты»).
Вес — это функция от съеденных круассанов. Чем меньше съел, тем меньше весишь.
Расстояние — это функция времени. Чем дольше ты будешь идти, тем больше пройдешь.
Ну а теперь перейдем к одному из видов функций – линейной функции.
Линейная функция — коротко о главном
Линейная функция –это функция вида \( y=kx+b\), где \( k\) и \( b\) – любые числа (коэффициенты).
Рассмотрим, как коэффициенты влияют на месторасположение графика:
- \( k\) — отвечает за угол наклона графика (\( \displaystyle k=tg\alpha \))
- \( \displaystyle b\) — точка пересечения с \( \displaystyle Oy\)
Общие варианты представлены на рисунке:
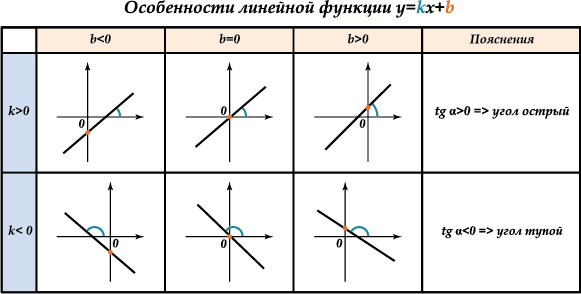
Линейная функция
Но сначала официальное определение «Функции» – теперь ты его поймешь. Держи в уме: деньги – зарплата, вес – круассаны, расстояние – время.
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Что значит «допустимому»?
Все дело в понятии «область определения»: для некоторых функций не все аргументы «одинаково полезны» — не все можно подставить в зависимость.
Например, для функции \( y=\sqrt{x}\) отрицательные значения аргумента \( x\) – недопустимы.
Ну и вернемся, наконец, к теме данной статьи.
Линейной называется функция вида \( y=kx+b\), где \( k\) и \( b\) – любые числа (они называются коэффициентами).
Другими словами, линейная функция – это такая зависимость, что функция прямо пропорциональна аргументу.
Как думаешь, почему она называется линейной?
Все просто: потому что графиком этой функции является прямая линия. Но об этом чуть позже.
Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения \( D\left( y \right)\) и область значений \( E\left( y \right)\).
Область определения линейной функции
Какими могут быть значения аргумента линейной функции \( y=kx+b\)? Правильно, любыми. Это значит, что область определения – все действительные числа:
\( D\left( y \right)=\mathbb{R}\)
или \( D\left( y \right)=\left( -\infty ;+\infty \right)\).
А множество значений?
Область значений линейной функции
Тут тоже все просто: поскольку функция прямо пропорциональна аргументу, то чем больше аргумент \( x\), тем больше значение функции \( y\).
Значит, \( y\) так же как и \( x\) может принимать все возможные значения, то есть \( E\left( y \right)=\mathbb{R}\), верно?
Верно, да не всегда. Есть такие линейные функции, которые не могут принимать любые значения. Как думаешь, в каком случае возникают ограничения?
Вспомним формулу: \( y=kx+b\). Какие нужно выбрать коэффициенты \( k\) и \( b\), чтобы значение функции y не зависело от аргумента \( x\)?
А вот какие: \( b\) – любое, но \( k=0\). И правда, каким бы ни был аргумент \( x\), при умножении на \( k=0\) получится \( 0\)!
Тогда функция станет равна \( y=0\cdot x+b=b\), то есть она принимает одно и то же значение при всех \( x\):
\( y = kx + b:{\rm{ }}\left[ \begin{array}{l}E\left( y \right) = \mathbb{R}{\rm{ при }}k \ne 0\\E\left( y \right) = \left\{ b \right\}{\rm{ при }}k = 0.\end{array} \right.\)Теперь рассмотрим несколько задач на линейную функцию.
Три задачи на линейную функцию
- При увеличении аргумента функции \( y=kx+b\) на \( 2\), функция увеличилась на \( 4\). Найдите коэффициент \( k\).
- При увеличении аргумента функции \( y=kx+b\) на \( 1\), функция уменьшилась на \( 3\). Найдите коэффициент \( k\).
- Дана функция \( y=kx+b\). При \( x=3:y=1\), а при \( x=5:y=-1\). Определите коэффициенты \( k\) и \( b\) функции.
Решение задачи №1
Пусть начальное значение аргумента равно некому числу \( {{x}_{1}}\). После увеличения на \( 2\) аргумент стал равен: \( {{x}_{2}}={{x}_{1}}+2\).
Чему была равна функция до увеличения? Подставляем аргумент в формулу:
Решение задачи №2
Аналогично предыдущей задаче:
Начальное значение аргумента равно \( {{x}_{1}}\), конечное – \( {{x}_{2}}={{x}_{1}}+1\).
Начальное значение функции: \( {{y}_{1}}=k{{x}_{1}}+b\);
конечное значение функции: \( {{y}_{2}}=k{{x}_{2}}+b=k\left( {{x}_{1}}+1 \right)+b=k{{x}_{1}}+k+b\).
В этот раз функция не увеличилась, а уменьшилась. Это значит, что конечное значение будет меньше начального, а значит, изменение (разность конечного и начального) будет отрицательным:
Определение прямой пропорциональной зависимости
Если проанализировать решения этих двух задач, можно прийти к важному выводу.
При изменении аргумента линейной функции на \( \Delta x\) функция изменяется на \( k\cdot \Delta x\). То есть изменение функции всегда ровно в \( \mathbf{k}\) раз больше изменения аргумента.
По сути это является определением прямой пропорциональной зависимости.
Решение задачи №3
Подставим известные значения аргумента и функции в формулу \( y=kx+b\):
\( 1=k\cdot 3+b\)
\( -1=k\cdot 5+b\)
Получили два уравнения относительно \( k\) и \( b\). Теперь достаточно решить систему этих двух уравнений:
График линейной функции
Как я уже упоминал ранее, график такой функции – прямая линия.
Как известно из геометрии, прямую можно провести через две точки (то есть, если известны две точки, принадлежащие прямой, этого достаточно, чтобы ее начертить).
Предположим, у нас есть функция линейная функция \( y=2x+1\). Чтобы построить ее график, нужно вычислить координаты любых двух точек.
То есть нужно взять любые два значения аргумента \( x\) и вычислить соответствующие два значения функции.
Затем для каждой пары \( \left( x;y \right)\) найдем точку в системе координат, и проведем прямую через эти две точки.
Проще всего найти функцию, если аргумент \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).
Итак, первая точка имеет координаты \( \left( 0;1 \right)\).
Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).
Вторая точка имеет координаты \( \left( 1;3 \right)\).
Ставим эти две точки на координатной плоскости:
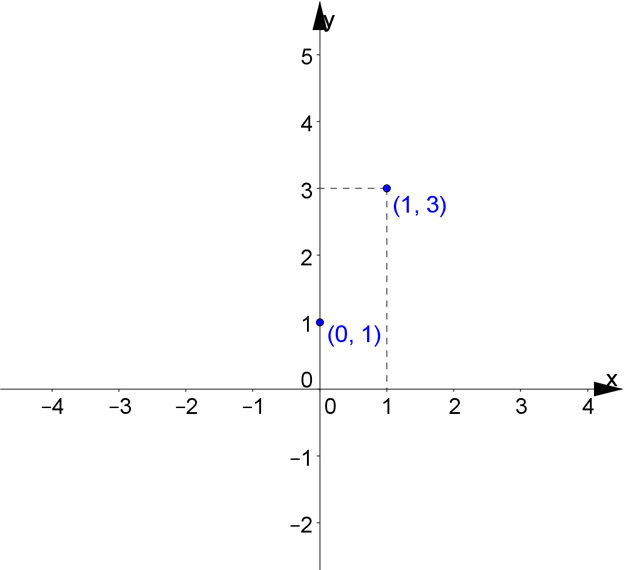
Теперь прикладываем линейку, и проводим прямую через эти две точки:
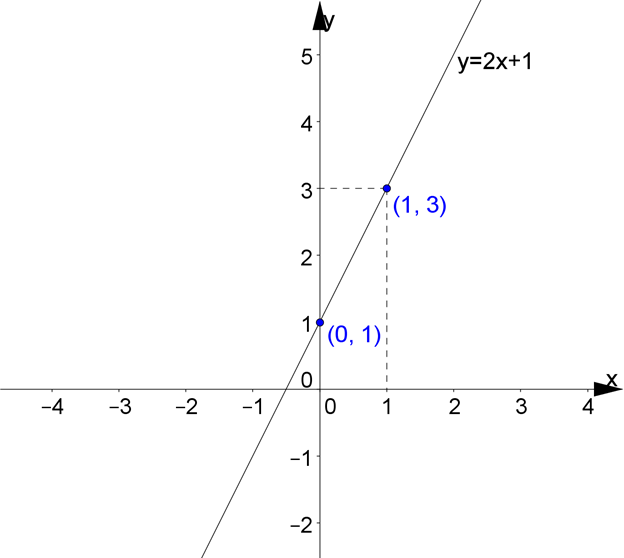
Вот и все, график построен!
Давай теперь на этом же рисунке построим еще два графика: \( y={x} -1\) и \( y=-x+2\).
Построй их самостоятельно так же: посчитай значение y для любых двух значений \( x\), отметь эти точки на рисунке и проведи через них прямую.
Должно получиться так:
Видно, что все три прямые по-разному наклонены и в разных точках пересекают координатные оси. Все дело тут в коэффициентах \( \displaystyle k\) и \( \displaystyle b\).
Давай разберемся, на что они влияют.
Коэффициенты линейной функции
Для начала выясним, что делает коэффициент \( \displaystyle b\). Рассмотрим функцию \( \displaystyle y=x+b\), то есть \( \displaystyle k=1\).
Меняя \( \displaystyle b\) будем следить, что происходит с графиком.
Итак, начертим графики для разных значений \( \displaystyle b:b=-2,\text{ -}1,\text{ }0,\text{ }1,\text{ }2\):
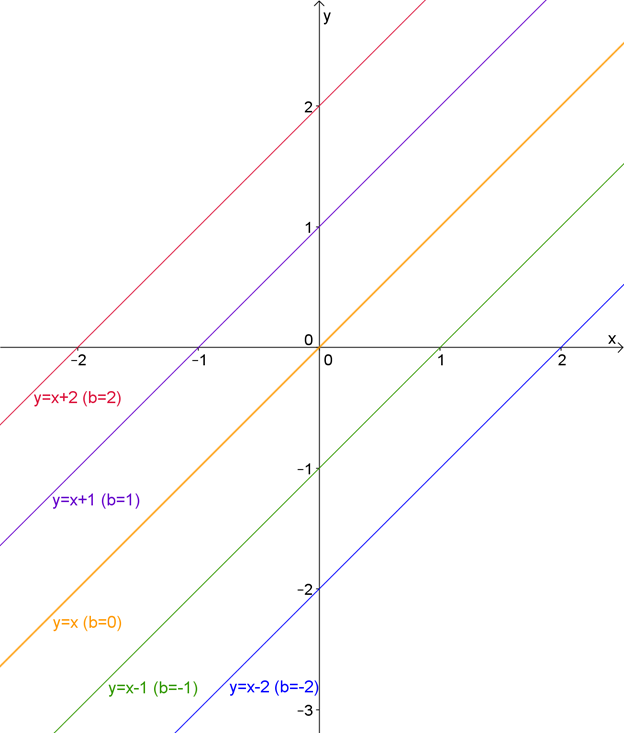
Что ты можешь сказать о них? Чем отличаются графики?
Это сразу видно: чем больше \( \displaystyle b\), тем выше располагается прямая.
Более того, заметь такую вещь: график пересекает ось \( \displaystyle \mathbf{y}\) в точке с координатой, равной \( \displaystyle \mathbf{b}\)!
И правда. Как найти точку пересечения графика с осью \( \displaystyle y\)? Чему равен \( \displaystyle x\) в такой точке?
В любой точке оси ординат (это название оси \( \displaystyle y\), если ты забыл) \( \displaystyle x=0\).
Значит достаточно подставить \( \displaystyle x=0\) в функцию, и получим ординату пересечения графика с осью \( \displaystyle y\):
\( \displaystyle y=k\cdot 0+b=b\)
Теперь по поводу \( \displaystyle k\). Рассмотрим функцию \( \displaystyle \left( b=0 \right).\) Будем менять \( \displaystyle k\) и смотреть, что происходит с графиком.
Построим графики для \( \displaystyle k=-3,\text{ -}1,\text{ }0,\text{ }1,\text{ }2:\)
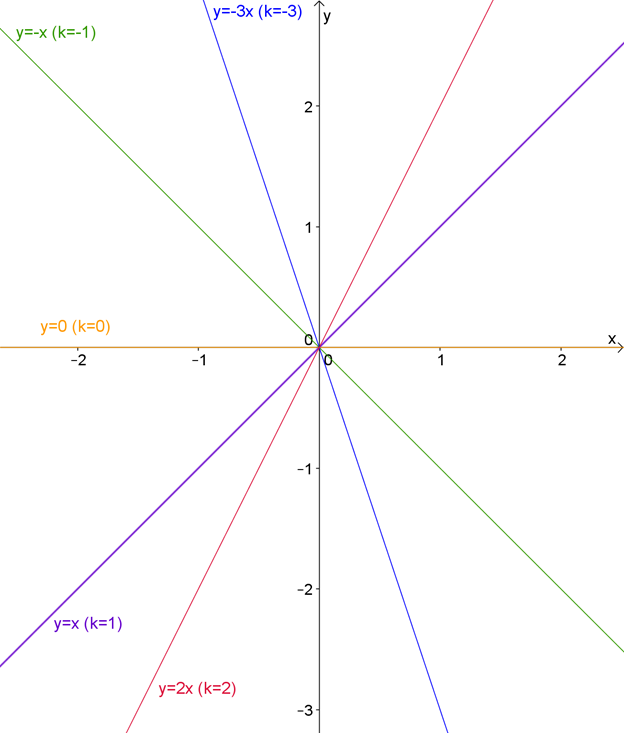
Так, теперь ясно: \( \displaystyle k\) влияет на наклон графика.
Чем больше \( \displaystyle k\) по модулю (то есть несмотря на знак), тем «круче» (под большим углом к оси абсцисс – \( \displaystyle Ox\)) расположена прямая.
Если \( \displaystyle k>0\), график наклонен «вправо», при \( \displaystyle k<0\) – «влево». А когда \( \displaystyle k=0\), прямая располагается вдоль оси абсциссс.
Давай разбираться. Начертим новый график \( \displaystyle y=kx+b\):
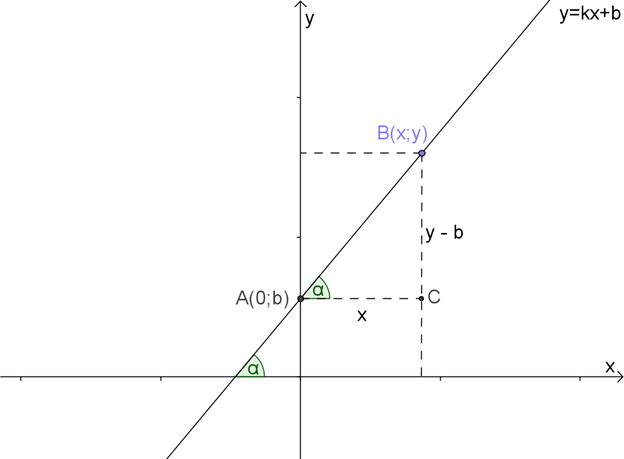
Выберем на графике две точки \( \displaystyle A\) и \( \displaystyle B\). Для простоты выберем точку \( \displaystyle A\) на пересечении графика с осью ординат. Точка \( \displaystyle B\) – в произвольном месте прямой, пусть ее координаты равны \( \displaystyle \left( x;y \right)\).
Рассмотрим прямоугольный треугольник \( \displaystyle ABC\), построенный на отрезке \( \displaystyle AB\) как на гипотенузе.
Из рисунка видно, что \( \displaystyle AC=x\), \( \displaystyle BC=y-b\).
Подставим \( \displaystyle y=kx+b\) в \( \displaystyle BC:BC=y-b=kx+b-b=kx\).
Получается, что \( BC = k \cdot AC{\rm{ }} \Rightarrow {\rm{ }}k = \frac{{BC}}{{AC}} = {\mathop{\rm tg}\nolimits} \alpha \).
Итак, коэффициент \( \displaystyle k\) равен тангенсу угла наклона графика, то есть угла между графиком и осью абсциссс.
Именно поэтому его (коэффициент \( \displaystyle k\)) обычно называют угловым коэффициентом.
В случае, когда \( k < 0,{\mathop{\rm tg}\nolimits} \alpha < 0,\) что соответствует тупому углу:
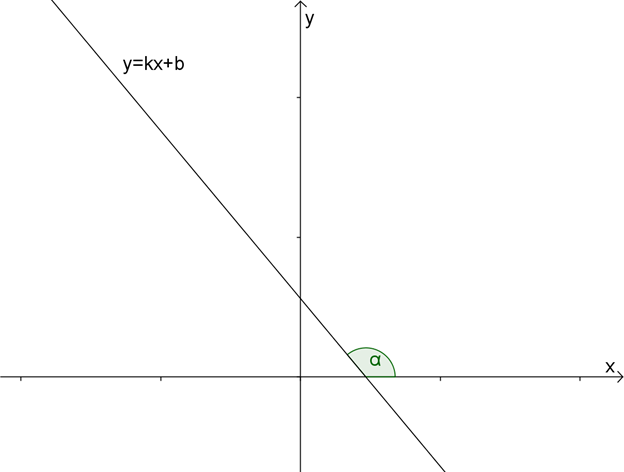
Если же \( \displaystyle k=0\), тогда и \( {\mathop{\rm tg}\nolimits} \alpha = 0,\) следовательно \( \displaystyle \alpha =0\), то есть прямая параллельна оси абсцисс.
Понимать геометрическое значение коэффициентов очень важно, оно часто используется в различных задачах на линейную функцию.
Разбор еще трех задач на линейную функцию
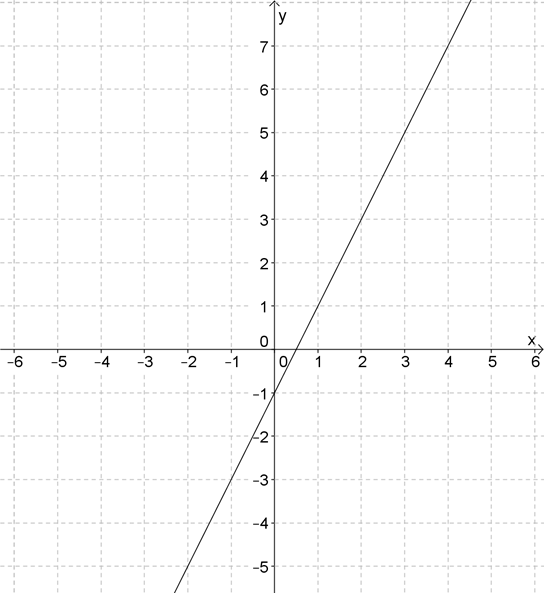
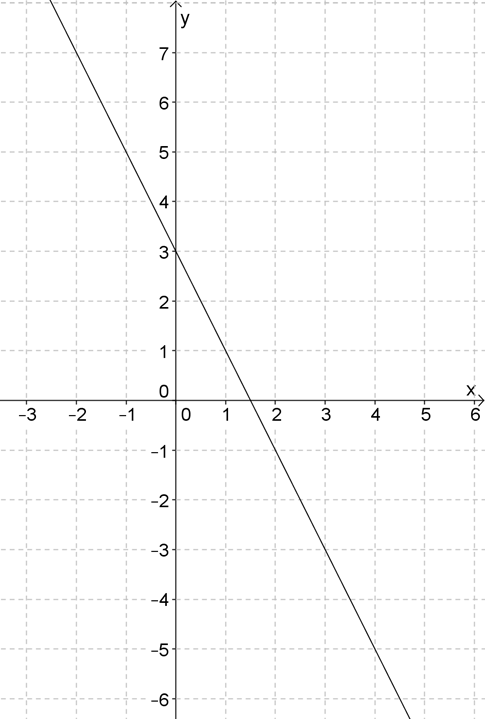
1. Найдите коэффициенты \( \displaystyle k\) и \( \displaystyle b\) линейной функции, график которой приведен на рисунке. Запишите уравнение этой функции.
2. Найдите коэффициенты \( \displaystyle k\) и \( \displaystyle b\) линейной функции, график которой приведен на рисунке. Запишите уравнение этой функции.
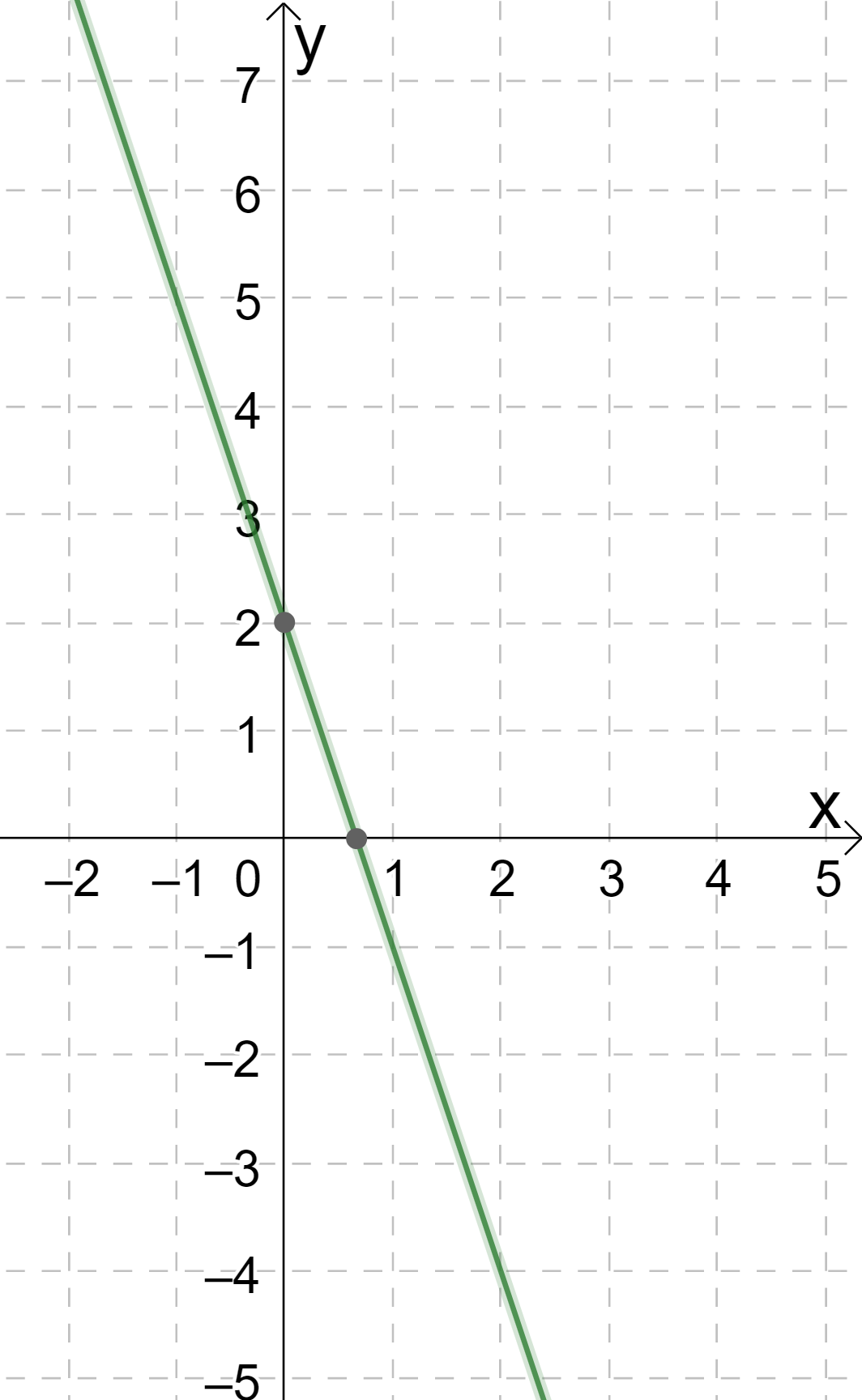
3. График какой из функций изображен на рисунке?
a) \( y=-2x+3\)
b) \( y=2x+3\)
c) \( y=3x+2\)
d) \( y=-3x+3\)
Решение задачи №1
Коэффициент \( b\) найти проще простого – это ведь точка пересечения графика с осью \( \displaystyle Oy\):
\( \displaystyle b=-1\)
Угловой коэффициент \( \displaystyle k\) – это тангенс угла наклона прямой.
Для его нахождения выберем две точки \( \displaystyle A\) и \( \displaystyle B\) на графике и построим прямоугольный треугольник с гипотенузой \( \displaystyle AB\):
Решение задачи №2
Все аналогично предыдущей задаче.
\( b=2\)
Поскольку график наклонен «влево», угол между ним и осью абсцисс тупой, а значит, угловой коэффициент отрицательный.
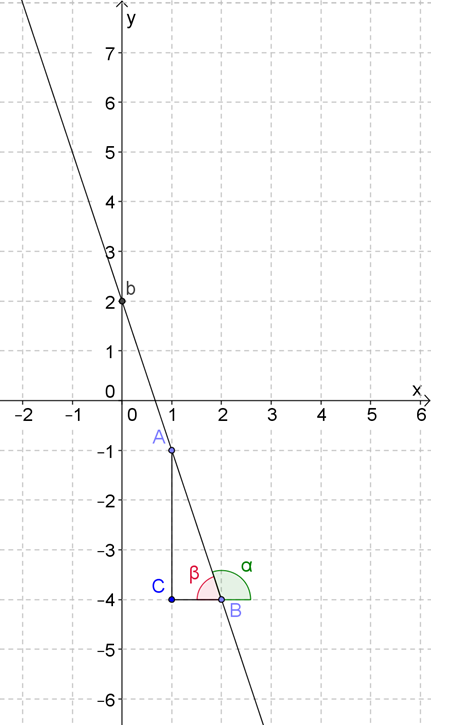
Чтобы было проще найти тангенс угла наклона \( \alpha \), рассмотрим смежный с ним угол \( \beta \).
Тангенсы смежных углов равны по модулю, и противоположны по знаку:
Решение задачи №3
И снова в первую очередь смотрим на \( \displaystyle b:b=3\). Значит, есть смысл рассматривать только функции a), b) и d).
Теперь посмотрим, каким должен быть угловой коэффициент?
Во-первых, он должен быть отрицательным, значит, выбрасываем ответ b). Остается a) и d).
Чтобы выбрать из них, придется найти тангенс угла наклона графика:
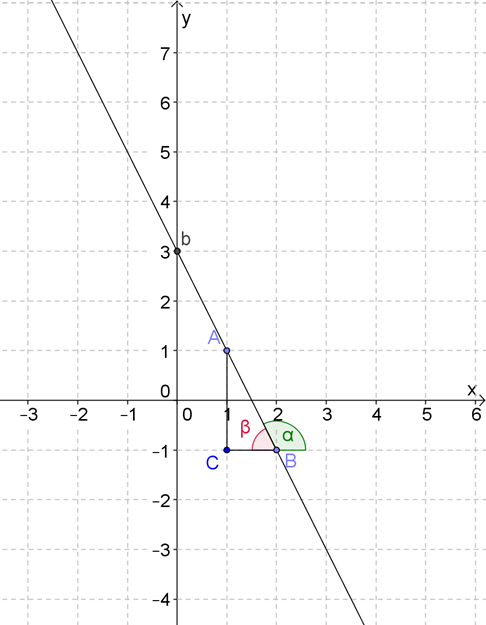
Отлично, значит уравнение этой прямой выглядит так:
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)
Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.
Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики.
На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях).
Мы рассмотрим:
- степенную функцию (линейную, квадратичную, обратную зависимость, корни),
- тригонометрические и обратные тригонометрические,
- показательную и
- логарифмическую функции.
Преобразования графиков функций. ЕГЭ 18. Задачи с параметром.
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



7 класс. Начала изучать линейную функцию. Понятнее еще не встречала объяснения, а перелопатила я немало ресурсов. Подскажите с какого класса можно приходить на подготовку к ГИА?
Я бы не выделял отдельно подготовку к ОГЭ (сейчас ГИА так называется). Куда важнее знать и понимать математику и развивать математическое мышление. Если все это будет, к ОГЭ подготовитесь в 9 классе быстро. А вот математическое мышление развивать нужно начинать чем раньше, тем лучше. Для этого этот учебник и создан )