ОДЗ. Область допустимых значений

ОДЗ – это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.

Например, если перед тобой уравнение $\displaystyle \sqrt{x}=y$ , то ни $\displaystyle x$ , ни $\displaystyle y$ не могут быть отрицательными:

$\displaystyle \left\{ \begin{array}{l}x\ge 0;\\y\ge 0.\end{array} \right.$

Часто в задачах бывает очень важно учесть ОДЗ и «вычеркнуть» те решения, которые на самом деле решениями не являются.

Иначе ты сделаешь глупую, очень глупую ошибку и не получишь то, что заслужил на ЕГЭ!

Читай эту статью и ты будешь знать об ОДЗ все!

ОДЗ — коротко о главном

ОДЗ – это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.

Функции, для которых важна ОДЗ:

Тип функции	ОДЗ
Обратная зависимость	$\displaystyle y=\frac{a}{x}:\text{ }x\ne 0$ .
Корень	$\displaystyle \sqrt{x}=y:\text{ }\left\{ \begin{array}{l}x\ge 0;\\y\ge 0.\end{array} \right.$
Показательная функция	$\displaystyle {{y}^{x}}=z:\text{ }\left\{ \begin{array}{l}y>0;\\z>0.\end{array} \right.$
Логарифмическая функция	$\displaystyle {{\log }_{x}}y=a:\text{ }\left\{ \begin{array}{l}x>0;\\x\ne 1;\\y>0.\end{array} \right.$
Тригонометрические функции	$\displaystyle -1\le \sin x\le 1;$ $\displaystyle -1\le \cos x\le 1;$ $y = {\mathop{\rm tg}\nolimits} x:{\rm{ }}x \ne \frac{\pi }{2} + \pi n,{\rm{ }}n \in \mathbb{Z};$ $y = {\mathop{\rm ctg}\nolimits} x:{\rm{ }}x \ne \pi n,{\rm{ }}n \in \mathbb{Z}{\rm{.}}$

ОДЗ (Область допустимых значений) — подробнее

Давай разберем пример, наглядно показывающий, что такое ОДЗ:

Решим уравнение $\displaystyle \sqrt{2x+3}=x$ .

Все очень просто, если ты уже освоил тему «Иррациональные уравнения».

Возводим левую и правую части уравнения в квадрат:

$\displaystyle 2x+3={{x}^{2}}\text{ }\Leftrightarrow \text{ }{{x}^{2}}-2{x}-3=0$ .

Теперь решаем квадратное уравнение. Я воспользуюсь теоремой Виета (если забыл, что это такое, – посмотри тему «Квадратные уравнения »).

Получаем корни:

$\displaystyle \left[ \begin{array}{l}x=3\\x=-1\end{array} \right.$

Вроде все? А давай-ка теперь сделаем проверку – подставим полученные значения в начальное уравнение:

$\displaystyle x=3:\text{ }\sqrt{2\cdot 3+3}=3\text{ }\Leftrightarrow \text{ }\sqrt{9}=3$ – все верно.

$\displaystyle x=-1:\text{ }\sqrt{2\cdot \left( -1 \right)+3}=-1\text{ }\Leftrightarrow \text{ }\sqrt{1}=-1$ – неверно! А все почему?

Да потому, что мы не учли ОДЗ!

По определению квадратный корень из любого числа не может быть отрицательным.

Значит, глядя на уравнение $\displaystyle \sqrt{2x+3}=x$ мы должны сразу же написать:

$\displaystyle \left\{ \begin{array}{l}x\ge 0;\\2x+3\ge 0.\end{array} \right.$

Если помнишь тему «Иррациональные уравнения», ты сразу скажешь, что второе условие в этой системе писать необязательно. И правда, мы ведь потом возведем все в квадрат, и получится, что $\displaystyle 2x+3={{x}^{2}}$ , а значит – автоматически неотрицательно.

Итак, с помощью этих рассуждений приходим к такой области допустимых значений:

$\displaystyle x\ge 0$ .

Тогда сразу становится ясно, что корень $\displaystyle x=-1$ не подходит. И остается единственный ответ $\displaystyle x=3$ .

Всего мы изучаем несколько разных функций, для которых важна ОДЗ. Вот они со своими ОДЗ в удобной табличке.

Функции, для которых важна ОДЗ

Тип функции	ОДЗ
Обратная зависимость	$\displaystyle y=\frac{a}{x}:\text{ }x\ne 0$ .
Корень	$\displaystyle \sqrt{x}=y:\text{ }\left\{ \begin{array}{l}x\ge 0;\\y\ge 0.\end{array} \right.$
Показательная функция	$\displaystyle {{y}^{x}}=z:\text{ }\left\{ \begin{array}{l}y>0;\\z>0.\end{array} \right.$
Логарифмическая функция	$\displaystyle {{\log }_{x}}y=a:\text{ }\left\{ \begin{array}{l}x>0;\\x\ne 1;\\y>0.\end{array} \right.$
Тригонометрические функции	$\displaystyle -1\le \sin x\le 1;$ $\displaystyle -1\le \cos x\le 1;$ $y = {\mathop{\rm tg}\nolimits} x:{\rm{ }}x \ne \frac{\pi }{2} + \pi n,{\rm{ }}n \in \mathbb{Z};$ $y = {\mathop{\rm ctg}\nolimits} x:{\rm{ }}x \ne \pi n,{\rm{ }}n \in \mathbb{Z}{\rm{.}}$

Рассмотрим примеры с каждой из этих функций:

ОДЗ обратной зависимости

$\displaystyle \frac{{{x}^{2}}}{{{\left( {x}-1 \right)}^{2}}}=\frac{x}{{{x}^{2}}-2x+1}$ .

Замечаем, что в знаменателе правой части формула сокращенного умножения:

$\displaystyle \frac{{{x}^{2}}}{{{\left( {x}-1 \right)}^{2}}}=\frac{x}{{{\left( {x}-1 \right)}^{2}}}$ .

ОДЗ: $\displaystyle {x}-1\ne 0\text{ }\Rightarrow \text{ }x\ne 1.$

Теперь можно спокойно избавляться от одинаковых знаменателей:

$\displaystyle {{x}^{2}}=x\text{ }\Leftrightarrow \text{ }x\left( {x}-1 \right)=0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}x=0\\x=1\end{array} \right.$

Согласно ОДЗ второй корень не подходит.

Ответ: $\displaystyle 0$ .

ОДЗ степенной функции

$\displaystyle \sqrt{2-x}=x$ .

Такой пример мы уже рассматривали, поэтому реши его самостоятельно.

Ответ: $\displaystyle 1$ .

ОДЗ показательной функции

$\displaystyle {{x}^{{{x}^{2}}-2x}}={{x}^{3}}$

Не пугайся, тут все просто:

ОДЗ: $\displaystyle x>0$

Обе части уравнения строго положительны, поэтому делим все на правую часть:

$\displaystyle \frac{{{x}^{{{x}^{2}}-2x}}}{{{x}^{3}}}=1\text{ }\Leftrightarrow \text{ }{{x}^{{{x}^{2}}-2{x}-3}}=1$

Теперь возможны два варианта: либо основание степени равно $\displaystyle 1$ , либо показатель равен $\displaystyle 0$ :

$\displaystyle \left[ \begin{array}{l}x=1\\{{x}^{2}}-2{x}-3=0\end{array} \right.\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}x=1\\x=3\\x=-1\end{array} \right.$

(квадратное уравнение реши сам)

Теперь вспомним ОДЗ: корень $\displaystyle x=-1$ – «сторонний».

Ответ: $\displaystyle 1;\text{ }3$ .

ОДЗ логарифмической функции

$\displaystyle {{\log }_{x}}\left( x+2 \right)=2$ .

ОДЗ: $\displaystyle \left\{ \begin{array}{l}x+2>0\\x>0\\x\ne 1\end{array} \right.\text{ }\Rightarrow \text{ }\left\{ \begin{array}{l}x>0\\x\ne 1.\end{array} \right.$

$\displaystyle {{\log }_{x}}\left( x+2 \right)=2\text{ }\Leftrightarrow \text{ }{{x}^{2}}=x+2\text{ }\Leftrightarrow \text{ }{{x}^{2}}-{x}-2=0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}x=-1\\x=2\end{array} \right.$

С учетом ОДЗ нужно отбросить отрицательный корень:

Ответ: $\displaystyle 2$ .

ОДЗ тригонометрической функции

$\displaystyle \frac{{{{\sin }^2}x}}{{\cos x}} = {\mathop{\rm tg}\nolimits} x$

ОДЗ: $\displaystyle x\ne \frac{\pi }{2}+\pi n,\text{ }n\in \mathbb{Z}$ .

Для наглядности изображу область допустимых значений на единичной окружности в виде выколотых точек:

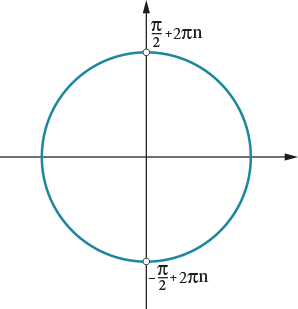
odz oblast dopustimyh znachenij trigonometriya

$\displaystyle \frac{{{{\sin }^2}x}}{{\cos x}} = {\mathop{\rm tg}\nolimits} x \Leftrightarrow \frac{{\sin x}}{{\cos x}} \cdot \sin x = {\mathop{\rm tg}\nolimits} x \Leftrightarrow {\mathop{\rm tg}\nolimits} x \cdot \sin x = {\mathop{\rm tg}\nolimits} x \Leftrightarrow {\mathop{\rm tg}\nolimits} x\left( {\sin x — 1} \right) = 0 \Leftrightarrow$

$\displaystyle \left[ \begin{array}{l}{\mathop{\rm tg}\nolimits} x = 0\\\sin x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \pi n,{\rm{ }}n \in \mathbb{Z}\\x = \frac{\pi }{2} + 2 \pi k,{\rm{ }}k \in \mathbb{Z}\end{array} \right.$

Очевидно, что вторая группа корней не подходит по ОДЗ.

Ответ: $\displaystyle x=\pi n,\text{ }n\in \mathbb{Z}$ .

Сдай ЕГЭ на 90+ с автором этого учебника

Алексей Шевчук — учитель с 20-летним стажем

математика, информатика, физика

Запишитесь на занятия:

+7 (905) 541-39-06

alexei.shevchuk@youclever.org

сотни моих учеников поступили в лучшие ВУЗы страны

автор самого понятного учебника по математике YouClever, по которому учатся десятки тысяч школьников и учителей;

закончил МФТИ, преподавал на малом физтехе;

профессиональный репетитор c 2003 года;

преподаю как на русском, так и на английском языках, готовлю к международным экзаменам;

в 2021 году сдал ЕГЭ на 100 баллов;

ОДЗ. Область допустимых значений

ОДЗ — коротко о главном

ОДЗ (Область допустимых значений) — подробнее