График линейной функции
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое линейная функция.
Начнем с небольшой проверки:
Если хоть один вопрос вызвал затруднения, прочти тему «Линейная функция».
Приступим к покорению линий и графиков!
График линейной функции — коротко о главном
График линейной функции – прямая линия. Прямую можно провести через две точки.
Чтобы построить график линейной функции вида y=kx+b, нужно:
- вычислить координаты любых двух точек (взять любые два значения аргумента x и вычислить соответствующие два значения y,
- для каждой пары ( x;y ) найти точку в системе координат, и провести прямую через эти две точки.
Рассмотрим пример для функции \( y=2x+1\):
Проще всего найти функцию, если аргумент: \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).
Итак, первая точка имеет координаты \( \left( 0;1 \right)\).
Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).
Вторая точка имеет координаты \( \left( 1;3 \right)\).
Угловой коэффициент \( \displaystyle k\) – это тангенс угла наклона прямой.
Для его нахождения выберем две точки \( \displaystyle A\) и \( \displaystyle B\) на графике и построим прямоугольный треугольник с гипотенузой \( \displaystyle AB\)
\( \displaystyle k=tg\alpha =\frac{BC}{AC}=\frac{2}{1}=2\)Построение графика линейной функции
Итак, ты уже умеешь обращаться с линейной функцией, анализировать ее график и строить его по точкам. Кстати, сколько нужно точек, чтобы построить график линейной функции?
Скажу сразу, эта тема настолько простая, что много нового ты здесь не выучишь. Но ты научишься не теряться во всяких нестандартных ситуациях.
Итак, дамы и господа, линейная функция:
\( \displaystyle y=kx+b\)
Построение графика линейной функции: ты берешь два каких-либо икса, (например, \( \displaystyle 0\) и \( \displaystyle 1\)), подставляешь их в формулу, находишь соответствующие игреки.
Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо.
Но бывает, что функция задана по-другому, например, неявно. Сейчас разберем, как быстро справляться с такими ситуациями.
Пример неявно заданной линейной функции
Постройте график уравнения \( \displaystyle 2y+3x=6\).
Ну а что тут сложного? Чтобы произвести построение графика линейной функции выражаем y и строим по точкам.
Это да, но можно сделать проще и интересней!
Выясним, в какой точке эта прямая будет пересекать ось \( \displaystyle Ox\).
Что характерно для этой точке? Правильно, \( \displaystyle y=0\). Так и пишем:
\( \displaystyle 2\cdot 0+3x=6\text{ }\Rightarrow \text{ }x=2\)А теперь проделаем то же самое с другой осью: в какой точке график пересекает ось \( \displaystyle Oy\)?
\( \displaystyle x=0\text{ }\Rightarrow \text{ }2y+3\cdot 0=6\text{ }\Rightarrow \text{ }y=3\)Бум! Вот и они – две точки графика. Осталось только приложить линейку:
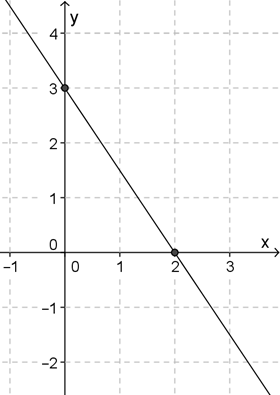
Согласись, это было быстро и просто!
А теперь сам:
\( \displaystyle 4x-5y=3\)Ладно, а как еще можно задать функцию?
Ну, например словесно:
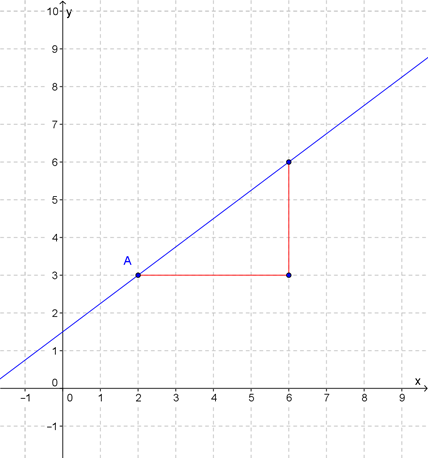
Прямая проходит через точку \( \displaystyle A\left( 2;3 \right)\), а ее угловой коэффициент равен \( \displaystyle 0,75\).
Ну что же, вспоминаем: что такое угловой коэффициент?
Что такое угловой коэффициент
Это, с одной стороны, коэффициент при \( \displaystyle x\), а с другой – это тангенс угла между прямой и осью \( \displaystyle Ox\).
Вот это мы и используем когда делаем построение графика линейной функции: ставим точку \( \displaystyle A\), и рисуем прямоугольный треугольник так, что один его катет параллелен оси \( \displaystyle Ox\), а другой – перпендикулярен.
При этом второй катет должен быть ровно в \( \displaystyle 0,75\) раз больше первого.
Очень удобно в этом случае, чтобы первый катет был равен \( \displaystyle 4\), тогда второй будет равен \( \displaystyle 3\):
4 примера построения графика линейных функций
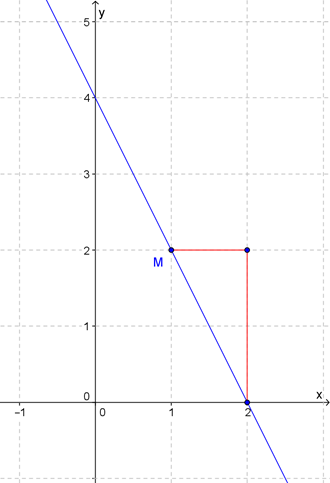
Пример №1
Прямая, уравнение которой имеет вид \( y=-2x+b\) (\( b\) неизвестно), проходит через точку \( M\left( 1;2 \right)\). Постройте ее.
Справился?
Должно получиться вот так:
Пример №2
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).
Строить график прямой \( y=-1,5x+1\) нельзя.
О, это что-то новенькое. Про параллельность прямых мы еще не учили.
Но как обычно, все просто. Нарисуем несколько параллельных прямых на координатной плоскости:
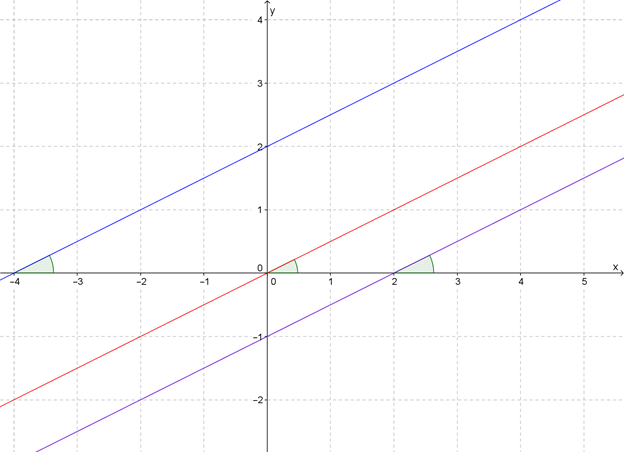
Что у них общего? Вообще, какие параметры важны для графиков? Конечно же, коэффициенты \( k\) и \( b\).
И сразу становится ясно: раз \( k\) отвечает за наклон, а наклон у них одинаковый (это же параллельные прямые, а ось \( Ox\) – секущая), значит, у них одинаковый коэффициент \( k\)!
Вернемся к задаче. Напомню условие:
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).
Итак, угловой коэффициент нашей прямой \( y=-1,5x+1\) равен угловому коэффициенту прямой , то есть \( -1,5\). Теперь задача становится точь в точь как мы решали до этого:
Пример №3
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( -1;2 \right)\) и параллельной прямой \( y=2x+8\).
Строить график прямой \( y=2x+8\) нельзя.
Ответ: \( y=2x+4\).
Пример №4
И еще один тип прямых. Самый простой из всех.
\( y=\frac{{{x}^{2}}-1}{x+1}\)Хм… Даже на линейную функцию непохоже, чего это он самый простой?
А вот почему: достаточно небольшого преобразования, и получится самая обычная линейная функция:
\( y=\frac{{{x}^{2}}-1}{x+1}=\frac{\left( x-1 \right)\left( x+1 \right)}{x+1}=x-1\)Вот и все!
А, нет, не все… еще ведь ОДЗ: на ноль делить нельзя, бла бла бла…
Ладно, ничего сложного здесь нет: \( x+1\ne 0\text{ }\Rightarrow \text{ }x\ne -1\).
Это и есть все отличие от обычной прямой: просто надо будет выколоть из графика одну точку: \( y=x-5\).
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)
Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.
Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики.
На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях).
Мы рассмотрим:
- степенную функцию (линейную, квадратичную, обратную зависимость, корни),
- тригонометрические и обратные тригонометрические,
- показательную и
- логарифмическую функции.
Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Нелли
09 мая 2019
Спасибо
Александр (админ)
09 мая 2019
Пожалуйста, Нелли. Удачи на экзаменах!
Мм
25 ноября 2019
Я учусь в 7 классе и т.к меня не было много дней я не мог самостоятельно понять тему по книге.
Александр (админ)
05 мая 2020
И какова дальше эта история, Мм? Вы разобрались с этой темой? С помощью нашего учебника?
ыпрчпатсап
05 мая 2020
ееееееееееееее пятёрка!!!!!!