Расстояние от точки до прямой
Это совсем короткая тема. И совсем не сложная.
Но она очень полезная в решении задач по стереометрии!
Более того, БОЛЬШИНСТВО задач стереометрии просят тебя найти какое-то расстояние в пространстве. Между диагональю и точкой, например…
Читай эту статью и сможешь без труда найти расстояние от точки до прямой!
Как найти расстояние от точки до прямой в пространстве?
Чтобы найти расстояние от точки до прямой в пространстве, нужно из этой точки опустить перпендикуляр на прямую и найти длину этого перпендикуляра.
Вот так:

В задачах, как правило, отрезок \(\displaystyle AH\) – это высота какой-либо фигуры (чаще всего – треугольника).
Давай убедимся в этом на примерах.
Задача:
Дан куб \( \displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\) с ребром, равным \( \displaystyle 2\).
Найти расстояние от точки \( \displaystyle {{A}_{1}}\) до прямой \( \displaystyle D{{C}_{1}}\).
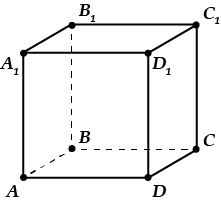
Решаем:
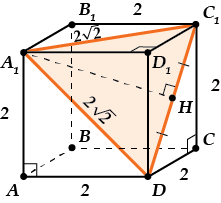
Первым делом организуем треугольник. Как?
Да очень просто – соединим точку \( \displaystyle {{A}_{1}}\) с точками \( \displaystyle D\) и \( \displaystyle {{C}_{1}}\).
Так можно делать в любой задаче, потому что любые три точки лежат в одной плоскости.
Итак, получился треугольник \( \displaystyle {{A}_{1}}{{C}_{1}}D.\)
Теперь найдем требуемое расстояние от точки до прямой:
Чтобы найти расстояние от точки \( \displaystyle {{A}_{1}}\) до прямой \( \displaystyle D{{C}_{1}}\), теперь достаточно найти высоту \( \displaystyle {{A}_{1}}H\) в \( \displaystyle \Delta {{A}_{1}}{{C}_{1}}D.\)
Что же это за треугольник? Смотри внимательно:
\( \displaystyle {{A}_{1}}{{C}_{1}}\) – диагональ квадрата со стороной \( \displaystyle 2\), значит \( \displaystyle {{A}_{1}}{{C}_{1}}^{2}={{2}^{2}}+{{2}^{2}}=8\), то есть \( \displaystyle {{A}_{1}}{{C}_{1}}=2\sqrt{2}\).
Но \( \displaystyle {{A}_{1}}D\) – тоже диагональ квадрата со стороной \( \displaystyle 2\), значит \( \displaystyle {{A}_{1}}{{D}^{2}}={{2}^{2}}+{{2}^{2}}=8\); \( \displaystyle {{A}_{1}}D=2\sqrt{2}\).
А \( \displaystyle D{{C}_{1}}\)? Конечно же , и это диагональ квадрата со стороной \( \displaystyle 2\), поэтому \( \displaystyle D{{C}_{1}}^{2}={{2}^{2}}+{{2}^{2}}=8\); \( \displaystyle D{{C}_{1}}=2\sqrt{2}\).
Что вышло? Равносторонний треугольник получился!
\( \displaystyle {{A}_{1}}{{C}_{1}}={{A}_{1}}D=D{{C}_{1}}=2\sqrt{2}\).
Значит, \( \displaystyle AH\) — не только высота, но и медиана, \( \displaystyle H{{C}_{1}}=\frac{D{{C}_{1}}}{2}=\frac{2\sqrt{2}}{2}=\sqrt{2}\).
Осталось применить теорему Пифагора:
\( \displaystyle {{A}_{1}}{{H}^{2}}={{A}_{1}}{{C}_{1}}^{2}-H{{C}_{1}}^{2}={{\left( 2\sqrt{2} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}=6\).
Следовательно, расстояние от точки до прямой равно:
\( \displaystyle {{A}_{1}}H=\sqrt{6}\).
Задача решена. И теперь глянь как можно подготовиться к ЕГЭ…
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org


