5 способов разложения многочлена на множители
Для чего нужно раскладывать многочлен на множители?
Чтобы облегчить себе жизнь! После того как ты это сделаешь, выражение станет намного проще и ты легко сможешь с ним «разобраться»!
Ты как бы делишь одну большую и сложную проблему, на несколько маленьких и простых и потом разбираешься с каждой маленькой проблемой по отдельности.
Как этому научиться?
Прочитай эту статью. Сначала мы разберем что означают все «сложные» слова.
Потом объясним все пять способов разложения многочлена на множители.
И затем разберем на примерах как это делать.
Let’s dive right in… (Поехали!) 🙂
Существует 5 основных способов разложения многочлена на множители:
- вынесение общего множителя за скобки;
- использование формул сокращенного умножения;
- метод группировки;
- метод выделения полного квадрата;
- разложение квадратного трехчлена на множители.
Основные определения (разбираемся со «сложными» словами)
Одночлены
Одночленами могут быть числа, переменные, произведения чисел и переменных, а так же переменные в степени (если забыл, что такое степень, посмотри тему «Степень и ее свойства»)
Например:
- \( 4\)
- \( x\)
- \( 4x\)
- \( 4{{x}^{2}}\)
- \( 4{{x}^{2}}y\)
Все это – одночлены. Видишь у них нет знаков «+» или «-«, как бы нет других членов.
Многочлены
Многочлен – это выражение, состоящее из суммы (или разности) нескольких одночленов различного вида:
- \( 4{{x}^{2}}+9x\)
- \( 2{{x}^{3}}-16{{x}^{2}}+4x\)
- \( 8x\cdot 4{{y}^{2}}-12+4{{x}^{2}}y-3{{y}^{2}}\cdot {{x}^{4}}+6-5{{y}^{2}}{{x}^{4}}\)
Множители
Так, ну давай по порядку. Как нетрудно догадаться, слово «множитель» происходит от слова «умножать».
Возьмем, например, число \( 12\), разложить его на множители означает расписать его в виде «умножения» или, как принято говорить в математике «произведения» множителей.
Так \( 12\) мы можем получить, умножив \( 2\) на \( 6\).
А \( 6\), в свою очередь, можно представить как произведение \( 2\) и \( 3\).
Чтоб было более наглядно, обратимся к картинке:
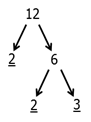
На картинке мы видим пошаговое разложение на множители, те которые подчеркнуты – это множители, которые дальше разложить уже нельзя.
То есть их нельзя уже представить в виде произведения (можно конечно представить каждое из них как единица, умноженная на само число, но это нам ничего не дает).
Я обещал, что картинка все разъяснит, ну разве из нее не понятно, что, \( 12=2\cdot 6\), а \( 6=2\cdot 3\)?
Вот и я говорю, что элементарно!
Иными словами, \( 2\cdot 2\cdot 3=12\).
Тут \( 2\), еще раз \( 2\) и \( 3\) – это и есть множители, на которые мы раскладываем.
Зачем нужно раскладывать многочлен на множители?
Это самый главный вопрос. Я уже говорил – чтобы облегчить тебе жизнь.
Раскладывая многочлен на множители, ты упрощаешь выражение! Ты как бы делишь одну большую и сложную проблему, на несколько маленьких и простых и потом разбираешься с каждой маленькой проблемой по отдельности.
А теперь «официальное» определение.
Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. При этом каждый множитель может быть как многочленом, так и одночленом.
Для чего нужно знать все пять способов?
Потому что нет универсального способа, подходящего для всех многочленов.
Давай посмотрим на каждый из них…
5 способов разложения многочлена на множители
1. Вынесение общего множителя за скобки
\( \displaystyle ac+bc=c(a+b)\)2. Формулы сокращенного умножения
\( \begin{array}{l}\left[ 1 \right]\ \ \ \ {{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\\\left[ 2 \right]\ \ \ \ {{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\\\left[ 3 \right]\ \ \ \ {{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)\\\left[ 4 \right]\ \ \ \ {{\left( a+b \right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\\\left[ 5 \right]\ \ \ \ {{\left( a-b \right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\\\left[ 6 \right]\ \ \ \ {{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\\\left[ 7 \right]\ \ \ \ {{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\end{array}\)3. Метод группировки
Применяется если преобразование не очевидно. Здесь, например, можно переставить второй член на другое место:

\( {{x}^{3}}-5{{x}^{2}}y-3xy+15{{y}^{2}}\)
Группируем члены парами, получаем:
\( ({{x}^{3}}-5{{x}^{2}}y)-(3xy-15{{y}^{2}})\)
\( {{x}^{2}}(x-5y)-3y(x-5y)\)
\( ({{x}^{2}}-3y)(x-5y)\)
4. Выделение полного квадрата
Можно преобразовать многочлен и привести к виду разности квадратов, например и применить формулу сокращенного умножения
\( {{x}^{4}}-4{{x}^{2}}-1=\underbrace{{{x}^{4}}-2\cdot 2\cdot {{x}^{2}}+4}_{\text{ }{{\left( {{x}^{2}}-2 \right)}^{2}}}-4-1={{\left( {{x}^{2}}-2 \right)}^{2}}-5=\left( {{x}^{2}}-2+\sqrt{5} \right)\left( {{x}^{2}}-2-\sqrt{5} \right)\)5. Разложение квадратного трехчлена на множители
Квадратный трехчлен – многочлен вида
\( a{{x}^{2}}+bx+c=0\)Теорема. Если квадратное уравнение \( a{{x}^{2}}+bx+c=0\) имеет корни \( {{x}_{1}},\text{ }{{x}_{2}}\), то его можно записать в виде:
\( a{{x}^{2}}+bx+c=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)\).
Подробнее о каждом из 5-ти способов разложения на множители
1. Вынесение общего множителя за скобки
Это один из самых элементарных способов упростить выражение. Для применения этого метода давай вспомним распределительный закон умножения относительно сложения (не пугайся этих слов, ты обязательно знаешь этот закон, просто мог забыть его название).
Закон гласит:
Чтобы сумму двух чисел умножить на третье число, нужно каждое слагаемое умножить на это число и полученные результаты сложить.
Иначе говоря, \( a\left( b\text{ }+\text{ }c \right)\text{ }=\text{ }ab\text{ }+\text{ }ac\).
Так же можно проделать и обратную операцию, \( ab\text{ }+\text{ }ac\text{ }=\text{ }a\left( b\text{ }+\text{ }c \right)\).
Вот именно эта обратная операция нас и интересует. Как видно из образца, общий множитель а, можно вынести за скобку.
Подобную операцию можно проделывать как с переменными, такими как \( x\) и \( y\), например, так и с числами: \( 6\text{ }+\text{ }8\text{ }=\text{ }2\left( 3\text{ }+\text{ }4 \right)\).
Да, это слишком элементарный пример, так же, как и приведенный ранее пример, с разложением числа \( 12\), ведь все знают, что числа \( 6\), \( 8\) и \( 12\) делятся на \( 2\).
А как быть, если вам досталось выражение посложнее:
\( 3xy+123y\)?
Как узнать на что, например, делится число \( 123\).
Нееет! С калькулятором-то любой сможет, а без него слабо?
А для этого существуют признаки делимости, эти признаки действительно стоит знать, они помогут быстро понять, можно ли вынести за скобку общий множитель.
Признаки делимости
Запомнить их не так сложно, скорее всего, большинство из них и так тебе были знакомы, а что-то будет новым полезным открытием, подробнее в таблице:
| Делится на: | Признак делимости числа на данный делитель |
|---|---|
| 2 | Оканчивается на: 0, 2, 4, 6, 8 |
| 3 | Сумма цифр делится на 3 |
| 4 | Две последние цифры делятся на 4 |
| 5 | Последняя цифра 5 или 0 |
| 7 | Разность между числом десятков и удвоенной цифрой единиц делится на семь |
| 9 | Сумма цифр делится на 9 |
| 10 | Последняя цифра – ноль |
| 11 | Разность между суммой цифр, стоящих на нечетных местах, и суммой цифр, стоящих на четных местах, делится на 11 |
Что ж, вернемся к выражению \( 3xy+123y\), может вынести за скобку \( y\) да и хватит с него?
Нет, у математиков принято упрощать, так по полной, выносить ВСЕ, что выносится!
И так, с игреком все понятно, а что с числовой частью выражения? Оба числа нечетные, так что на \( 2\) разделить не удастся.
Можно воспользоваться признаком делимости на \( 3\), сумма цифр \( 1\), \( 2\) и \( 3\), из которых состоит число \( 123\), равна \( 6\), а \( 6\) делится на \( 3\), значит и \( 123\) делится на \( 3\).
Зная это, можно смело делить в столбик, в результате деления \( 123\) на \( 3\) получаем \( 41\) (признаки делимости пригодились!).
Таким образом, число \( 3\) мы можем вынести за скобку, так же, как y и в результате имеем:
\( 3xy\text{ }+\text{ }123y\text{ }=\text{ }3y\cdot \left( x\text{ }+\text{ }41 \right)\).
Чтобы удостовериться, что разложили все верно, можно проверить разложение, умножением!
Также общий множитель можно выносить и в степенных выражениях.
Вот тут, например, \( 2{{x}^{3}}-16{{x}^{2}}+4x\), видишь общий множитель?
У всех членов этого выражения есть иксы – выносим, все делятся на \( 2\) – снова выносим, смотрим что получилось: \( 2{{x}^{3}}-16{{x}^{2}}+4x=2x({{x}^{2}}-8x+2)\).
2. Формулы сокращенного умножения
Формулы сокращенного умножения уже упоминались в теории, если ты с трудом помнишь что это, то тебе стоит освежить их в памяти «Формулы сокращенного умножения».
А вот здесь можно решить вместе с нашим репетитором Алексеем Шевчуком 119 задач на формулы сокращенного умножения!
А вот здесь наше видео о том, какой навык, относящийся к формулам сокращенного умножения является самым сложным и самым важным — выделение полного кавдрата!
Справка.
Эти видео — часть нашего курса подготовки к ЕГЭ по математике. Можно провести бесплатный «тест-драйв» этого курса. Например, посетить наши пробные вебинары.
В чем суть разложения на множители с помощью формул сокращенного умножения?
Суть этого разложения в том, что бы заметить в имеющемся перед тобой выражении какую-то определенную формулу, применить ее и получить, таким образом, произведение чего-то и чего-то, вот и все разложение.
Формулы сокращенного умножения (таблица)
А теперь попробуй, разложи на множители следующие выражения, используя приведенные выше формулы:
- \( \displaystyle 16{{b}^{2}}-8b+1\)
- \( \displaystyle -42c+9{{c}^{2}}+49\)
- \( \displaystyle {{\left( 5\text{a} \right)}^{2}}-3\)
- \( \displaystyle \frac{\left( 4\text{a}+2\text{b} \right)\cdot \left( 4\text{a}-2\text{b} \right)}{16{{\text{a}}^{2}}+4{{\text{b}}^{2}}-16\text{ab}}\)
- \( \displaystyle {{\left( 3\text{a} \right)}^{3}}-1\)
Вот что должно было получиться:
3. Метод группировки
А вот тебе еще примерчик:
\( \displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}\)
Ну и что с ним делать будешь? Вроде бы и на \( \displaystyle 3\) что-то делится и на \( \displaystyle 5\), а что-то на \( \displaystyle x\) и на \( \displaystyle y\)
Но все вместе на что-то одно не разделишь, ну нет тут общего множителя, как не ищи, что, так и оставить, не раскладывая на множители?
Тут надо смекалку проявить, а имя этой смекалке – группировка!
Применяется она как раз, когда общие делители есть не у всех членов. Для группировки необходимо найти группки слагаемых, имеющих общие делители и переставить их так, чтобы из каждой группы можно было получить один и тот же множитель.
Переставлять местами конечно не обязательно, но это дает наглядность, для наглядности же можно взять отдельные части выражения в скобки, их ставить не запрещается сколько угодно, главное со знаками не напутать.
Не очень понятно все это? Объясню на примере:
В многочлене \( \displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}\) ставим член – \( \displaystyle 3xy\) после члена – \( \displaystyle 5x2y\) получаем:
\( \displaystyle {{x}^{3}}-5{{x}^{2}}y-3xy+15{{y}^{2}}\)
Группируем первые два члена вместе в отдельной скобке и так же группируем третий и четвертый члены, вынеся за скобку знак «минус», получаем:
А теперь смотрим по отдельности на каждую из двух «кучек», на которые мы разбили выражение скобками.
Хитрость в том, чтоб разбить на такие кучки, из которых можно будет вынести максимально большой множитель, либо, как в этом примере, постараться сгруппировать члены так, чтобы после вынесения из кучек множителей за скобку у нас внутри скобок оставались одинаковые выражения.
Из обеих скобок выносим за скобки общие множители членов, из первой скобки \( \displaystyle {{x}^{2}}\), а из второй \( \displaystyle 3y\), получаем:
\( \displaystyle {{x}^{2}}(x-5y)-3y(x-5y)\)
Но это же не разложение!
После разложения должно остаться только умножение, а пока у нас многочлен просто поделен на две части…
НО! Этот многочлен имеет общий множитель. Это \( \displaystyle (x-5y)\)
\( \displaystyle (x-5y)\)за скобку и получаем финальное произведение \( \displaystyle ({{x}^{2}}-3y)(x-5y)\)
Бинго! Как видишь, тут уже произведение и вне скобок нет ни сложения, ни вычитания, разложение завершено, т.к. вынести за скобки нам больше нечего.
Может показаться чудом, что после вынесения множителей за скобки у нас в скобках остались одинаковые выражения \( \displaystyle (x-5y)\), которые опять же мы и вынесли за скобку.
И вовсе это не чудо, дело в том, что примеры в учебниках и в ЕГЭ специально сделаны так, что большинство выражений в заданиях на упрощение или разложение на множители при правильном к ним подходе легко упрощаются и резко схлопываются как зонтик при нажатии на кнопку, вот и ищи в каждом выражении ту самую кнопку.
Что-то я отвлекся, что у нас там с упрощением? Замысловатый многочлен принял более простой вид: \( \displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}=({{x}^{2}}-3y)(x-5y)\).
Согласись, уже не такой громоздкий, как был?
4. Выделение полного квадрата
Иногда для применения формул сокращенного умножения (повтори тему «Формулы сокращенного умножения») необходимо преобразовать имеющийся многочлен, представив одно из его слагаемых в виде суммы или разности двух членов.
В каком случае приходится это делать, узнаешь из примера:
Многочлен \( \displaystyle {{x}^{2}}-4x+2\) в таком виде не может быть разложен при помощи формул сокращенного умножения, поэтому его необходимо преобразовать.
Возможно, поначалу тебе будет не очевидно какой член на какие разбивать, но со временем ты научишься сразу видеть формулы сокращенного умножения, даже если они не присутствуют не целиком, и будешь довольно быстро определять, чего здесь не хватает до полной формулы, а пока – учись, студент, точнее школьник.
Для полной формулы квадрата разности здесь нужно \( \displaystyle 4\) вместо \( \displaystyle 2\).
Представим третий член \( \displaystyle 2\) как разность \( \displaystyle 4-2\), получим: \( \displaystyle {{x}^{2}}-4x+4-2=({{x}^{2}}-4x+4)-2\)
К выражению в скобках можно применить формулу квадрата разности (не путать с разностью квадратов!!!), имеем: \( \displaystyle {{\left( x-2 \right)}^{2}}-2\), к данному выражению можно применить формулу разности квадратов (не путать с квадратом разности!!!), представив \( \displaystyle 2\), как \( \displaystyle \sqrt{2}\), получим: \( \displaystyle (x-2-\sqrt{2})(x-2+\sqrt{2})\).
Не всегда разложенное на множители выражение выглядит проще и меньше, чем было до разложения, но в таком виде оно становится более подвижным, в том плане, что можно не париться про смену знаков и прочую математическую ерунду.
Ну а вот тебе для самостоятельного решения, следующие выражения нужно разложить на множители.
Примеры:
- \( \displaystyle 25{{m}^{2}}-49{{n}^{2}};\)
- \( \displaystyle {{b}^{2}}-{{(a+1)}^{2}};\)
- \( \displaystyle {{(x-y)}^{2}}-{{(x+y+1)}^{2}};\)
- \( \displaystyle {{x}^{2}}+2{x}-3\)
- \( \displaystyle {{x}^{2}}+6x+5;\)
Решения:
5. Разложение квадратного трехчлена на множители
О разложении квадратного трехчлена на множители смотри далее в примерах разложения.
Примеры 5 способов разложения многочлена на множители
1. Вынесение общего множителя за скобки. Примеры
Помнишь, что такое распределительный закон? Это такое правило: \( \displaystyle ac+bc=c\left( a+b \right)\)
Пример 1:
Разложить многочлен на множители \( \displaystyle 10{{x}^{4}}-15{{x}^{3}}\).
Пример 2:
Разложи на множители \( \displaystyle 12{{y}^{3}}-2y\).
Решения двух примеров:
2. Формулы сокращенного умножения. Примеры
Чаще всего используем формулы разность квадратов, разность кубов и сумма кубов. Помнишь эти формулы? Если нет, срочно повтори тему «Формулы сокращенного умножения»!
Пример 1:
Разложите на множители выражение \( \displaystyle {{x}^{3}}-8{{y}^{6}}\).
Пример 2:
Разложите на множители многочлен \( \displaystyle {{x}^{4}}-1\).
Решение примеров 1 и 2:
3. Метод группировки. Примеры
Иногда можно поменять слагаемые местами таким образом, чтобы из каждой пары соседних слагаемых можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен превратится в произведение.
Пример:
Разложите на множители многочлен \( \displaystyle 2{{x}^{3}}+{{x}^{2}}y-6xy-3{{y}^{2}}\).
Решение:
4. Метод выделения полного квадрата. Примеры
Если многочлен удастся представить в виде разности квадратов двух выражений, останется только применить формулу сокращенного умножения (разность квадратов).
Пример:
Разложите на множители многочлен \( \displaystyle {{x}^{2}}+6{x}-7\).
Решение:
\( \begin{array}{*{35}{l}}{{x}^{2}}+6{x}-7=\underbrace{{{x}^{2}}+2\cdot 3\cdot x+9}_{квадрат\ суммы\ {{\left( x+3 \right)}^{2}}}-9-7={{\left( x+3 \right)}^{2}}-16= \\
=\left( x+3+4 \right)\left( x+3-4 \right)=\left( x+7 \right)\left( x-1 \right) \\
\end{array} \)
Пример:
Разложите на множители многочлен \( \displaystyle {{x}^{4}}-4{{x}^{2}}-1\).
Решение:
\( \begin{array}{*{35}{l}}{{x}^{4}}-4{{x}^{2}}-1=\underbrace{{{x}^{4}}-2\cdot 2\cdot {{x}^{2}}+4}_{квадрат\ разности{{\left( {{x}^{2}}-2 \right)}^{2}}}-4-1={{\left( {{x}^{2}}-2 \right)}^{2}}-5= \\
=\left( {{x}^{2}}-2+\sqrt{5} \right)\left( {{x}^{2}}-2-\sqrt{5} \right) \\
\end{array} \)
5. Разложение квадратного трехчлена на множители. Пример
Квадратный трехчлен – многочлен вида \( \displaystyle a{{x}^{2}}+bx+c=0\), где \( \displaystyle x\) – неизвестное, \( \displaystyle a\), \( \displaystyle b\), \( \displaystyle c\) – некоторые числа, причем \( \displaystyle a\ne 0\).
Значения переменной \( \displaystyle x\), которые обращают квадратный трехчлен в ноль, называются корнями трехчлена. Следовательно, корни трехчлена – это корни квадратного уравнения \( \displaystyle a{{x}^{2}}+bx+c=0\).
Если не помнишь, как находить эти корни, читай тему «Квадратные уравнения».
Теорема.
Если квадратное уравнение \( \displaystyle a{{x}^{2}}+bx+c=0\) имеет корни \( \displaystyle {{x}_{1}},\text{ }{{x}_{2}}\), то его можно записать в виде: \( \displaystyle a{{x}^{2}}+bx+c=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)\).
Пример:
Разложим на множители квадратный трехчлен: \( \displaystyle 2{{x}^{2}}+5x-3\).
Сначала решим квадратное уравнение: Теперь можно записать разложение данного квадратного трехчлена на множители:
\( \displaystyle \begin{array}{l}2{{x}^{2}}+5x-3=0.\\{{x}_{1,2}}=\frac{-5\pm \sqrt{{{5}^{2}}-4\cdot 2\cdot \left( -3 \right)}}{2\cdot 2}=\frac{-5\pm \sqrt{25+24}}{4}=\frac{-5\pm 7}{4};\\{{x}_{1}}=\frac{1}{2};\text{ }{{x}_{2}}=-3.\end{array}\)\( \displaystyle 2{{x}^{2}}+5x-3=2\left( x-\frac{1}{2} \right)\left( x+3 \right)\).
Подготовка к ЕГЭ на 90+ в мини-группах
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Разложить на множители x^4+2x+1
Аб+а^2? Разложить
Здравствуйте!
Помогите разложить на множители 128a⁷+b⁷.
Света, (2a)⁷+b⁷ = (2a+b)((2a)⁶ — (2a)⁵*b + (2a)⁴ * b² — (2a)³ * b³ + (2a)² * b⁴ — (2a) * b⁵ + b⁶)
Все замечательно. Но не могу разложить такое 15а^2 +14ab — 8b^2.
Ответ Алексея Шевчука:
Ирина, один из вариантов раскладывать подобные выражения — приравнять к нулю и решить квадратное уравнение относительно одной из переменных. Например, если за переменную считать a, то получится: D = 196b^2 + 480b^2 = 676b^2 = (26b)^2 => a = 2b/5 или a = -4b/3. Это даёт нам разложение 15(a — 2b/5)(a + 4b/3) = (5a — 2b)(3a + 4b).
Прекрасное изложение, спасибо! Успехов и продвижения вам!
Спасибо, Марьяна. Очень приятно слышать. И вам успехов и удачи!
1 из 100 сайтов нормальных
Спасибо, Захар. Заходите )
t^2*(t+12)^3-t*(t+12)^12*(t-6)^2 подскажите, пожалуйста, как разложить на множители
Здравствуйте, Татьяна!
Сначала давайте вынесем (t+12)^3, получим:
(t+12)^3(t^2 — t(t+12)^9(t-6)^2)
Смотрим на вторую скобку. Там у обеих частей есть t, вынесем:
t(t+12)^3(t — (t+12)^9(t-6)^2)
Я думаю, вторую скобку разложить больше не получится.
Спасибо за материал, а то везде дальше перечня и формул и примитивных примеров ничего нет. Подскажите, если можно, что делать с числителем.
5х^2-х-4/х^3-1 ???
Ирина, спасибо за отзыв. Я перешлю Алексею Шевчуку ваш вопрос, но он может не ответить. Сейчас очень загружены ((
Здравствуй, Ирина!
Давай начнем со знаменателя: внизу у тебя разность кубов, распиши ее по формуле (x^3-1^3=(x-1)(x^2+1*x*1^2))
Теперь посмотрим на числитель. Главная хитрость в том, что любой квадратный многочлен ax^2+bx+c (у тебя это 5x^2-x-4) можно представить в виде a(x-x1)(x-x2), где x1, x2 – решения квадратного уравнения.
То есть ты решаешь 5x^2-x-4=0, находишь его корни. Это -0.8 и 1, значит, ты можешь написать, что 5x^2-x-4=5(x-1)(x+0.8)
Как круто! Куб в знаменателе я тоже увидел конечно, а вот что делать с числителем не догадался ) Спасибо, Саша!
Некоторые комментарии прошлых лет к этой статье:
Гостинец
25 февраля 2018
Вау, я всю тему поняла! Поздравьте меня, подарите подарочки!!!!!!!!!!!!!!!
Александр (админ)
25 февраля 2018
Ну ты, крута! :)) От нас лучики счастья тебе! Хочешь понять еще лучше? Объясни кому-нибудь, кто не понимает.
Александр (Адин)
25 февраля 2018
Кстати, Гостинец, понять мало! Нужно обязательно набить руку. Нужно порешать примеры на эту тему. Причем чем быстрее ты это сделаешь, тем лучше закрепиться навык и на экзамене рука не дрогнет )) Возьми учебник и решай. Обязательно! Или можешь у нас на 100gia.ru Там все есть для подготовки к экзамену.
Геннадий
13 декабря 2018
Какой же Вы умница (без иронии!). Просто восхищаюсь. Самое ценное — с разъяснениями зачем нужно, что дает соответствующее знание.
(Админ)
28 января 2019
Спасибо, Геннадий. Поздно отвечаю, потому что поздно заметил. Но… доброе слово и кошке приятно! ) Еще раз спасибо!
Евгений
05 апреля 2019
а если сложные штуки попадутся и ни один метод не поможет.. (сложно просто догадаться будет). к примеру, y*y-x*y+4*x-7*y+12=0.. как бы не очевидно, вообще не очевидно. Сложный подход.
Александр (админ)
14 апреля 2019
Евгений, так, конечно, может быть. Но чем лучше ты подготовлен, чем больше задач решил, чем сложнее были задачи, которые ты сам решил, тем выше вероятность, что ты сможешь решить самые сложные задачи.
Когда ты находишь решение задач, ты приобретаешь навык не просто решать знакомые задачи, а находить решение сложных задач, которые ты никогда раньше не видел. И вполне возможно на экзамене именно так и случится: ты быстро решишь стандартные задачи и найдешь способ решить нестандартные в оставшееся время.
Любава
01 марта 2018
(x 2 −1 2 )(x 2 +1)мне непонятно это во 2 методе в последнем решении
Алексей Шевчук
03 марта 2018
Любава, это формула сокращённого умножения разность квадратов. Подробнее здесь: https://youclever.org/book/formuly-sokrashhennogo-umnozheniya-1#raznost-kvadratov
Рина
09 сентября 2018
4а^4+5а^2+1 Помогите пожалуйста
Александр (админ)
01 февраля 2019
Рина, это почти квадратное уравнение. Если бы уравнение было на самом деле квадратным, вот таким: 4а^2+5а+1 ты бы знала что с ним делать? А как его сделать таким? Подсказка: назови а^2 другой буквой, например b запиши новое уравнение и найди чему равно b…. Не забудь потом посчитать чему равно a.
Рина
09 сентября 2018
И спасибо!
Александр (админ)
11 февраля 2019
!!!
двоечник
11 февраля 2019
Что-то легко..
Александр (админ)
11 февраля 2019
Легко? В этом и цель. Спасибо.
Михаил
11 февраля 2019
Учась в школе, прорешал все задачи из задачника Сканави… Сейчас, спустя 17 лет, пытаюсь вспомнить основы 🙁
Александр (админ)
11 февраля 2019
Получается? )
Михаил
11 февраля 2019
Зачем все это нужно?
Александр (админ)
11 февраля 2019
Что «все это»? Математика?
Артем
11 февраля 2019
Завтра пробный экзамен по матану, пытаюсь вспомнить разложение на множители и формулы сокращенного умножения)
Александр (админ)
11 февраля 2019
Я так понимаю первый или второй курс университета? Да, Артем? Удачи!
Максим
11 февраля 2019
Почему в «Разложение на множители. Примеры методов разложения: 3. Метод группировки. Примеры.» после оборачивания в скобки у 3y^2 поменялся знак?
Алексей Шевчук
11 февраля 2019
Максим, за скобками знак «минус» — это значит, что мы вынесли множитель (-1). Легко проверить, правильный ли там знак: если раскроешь скобки обратно, должно получиться то, что было в начале.
Генадий
11 февраля 2019
Какой же Вы умница (без иронии!). Просто восхищаюсь. Самое ценное — с разъяснениями зачем нужно, что дает соответствующее знание.
Александр (админ)
11 февраля 2019
Спасибо, Генадий. Поздно отвечаю, потому что поздно заметил. Но… доброе слово и кошке приятно! ) Еще раз спасибо!
Ариадна
24 февраля 2019
Спасибо за материал. Действительно, ваш сайт очень помогает. Дальнейшего развития вам.
Александр (админ)
24 февраля 2019
Спасибо, Ариадна! И вам удачи во всех начинаниях!
Никита
27 февраля 2019
Здравствуйте, подскажите пожалуйста порядок решения 4 примера из примеров к подтеме «Формулы сокращенного умножения», никак не могу одолеть аналогичные уравнения.
Алексей Шевчук
27 февраля 2019
Никита, спасибо, в ответе были перепутаны знаки. На всякий случай, поясню как решать. Числитель у нас и так уже разложен на множители, осталось разложить знаменатель. Название подтемы — главная подсказка здесь: необходимо распознать и применить формулу сокращённого умножения, в данном случае это квадрат разности (4a-2b)^2. Дальше одну скобку сокращаем, затем выносим 2 за скобки в оставшихся числителе и знаменателе и сокращаем эту двойку.
Никита
28 февраля 2019
Благодарю
Алексей
09 мая 2019
a4 −12a3 +48a2 −64a это пример не на выделение полного квадрата, а на применение формулы куба разности. Поэтому этот пример лучше поместить в другой подраздел. Кроме того, хорошо бы добавить ещё одну полезную формулу сокращённого умножения: (x+a)(x+b)=x2+(a+b)x+ab.
Алексей Шевчук
23 мая 2019
Алексей, спасибо за замечание, теперь пример в нужном разделе. Формула (x+a)(x+b)=x2+(a+b)x+ab полезна, согласен, но это уже следующий уровень:) Пока что лучше эту формулу не запоминать, а использовать теорему Виета и формулу разложения квадратного трёхчлена на множители.
Сергей
09 июля 2019
Проверьте пожалуйста формулировку: Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. Превращающее сумму… Чего? А если многочлен — разность? Может я чего-то не понял?
Алексей Шевчук
13 июля 2019
Сергей, разность всегда можно представить как сумму с отрицательным слагаемым, например: 5-3 = 5+(-3). Поэтому выражения со знаками + или — называют общим словом «сумма».
Ксения
01 октября 2019
Великолепная статья! Спасибо огромное. Все стало на свои места. Все стало понятно!
Алексей Шевчук
15 октября 2019
Спасибо за отзыв, Ксения, очень рад, что учебник вам помогает
Ксенья
06 октября 2019
как можно разложить на множители 4^179+1. Помогите пожалуйста!!!
Алексей Шевчук
07 октября 2019
Сумма степеней порядка 2n + 1 (нечётных): x^(2n+1) + y^(2n+1) = (x + y) (x^(2n) – x^(2n–1)*y + x^(2n–2)*y^2 – …– x*y^(2n–1) + y^(2n)) = (4+1)(4^178-4^177+4^176-…-4+1) . К сожалению, короче не получится
Лисенок
09 октября 2019
Спасибо огромное за статью. Все понятно, и ровно столько сколько нужно, без лишней воды. Благодаря Вам я поняла наконец-то эту тему 🙂
Александр (админ)
09 октября 2019
Лисенок, как приятно слышать! И тебе спасибо! Удачи на всех экзаменах!
Алексей Шевчук
15 октября 2019
Очень рад, что статья помогла. Спасибо за отзыв!
ниважна
01 декабря 2019
ВАУ! Спасибо огромное ))просто в моем учебнике почему то не очень понятно)))а мама занята все время))))
Александр (админ)
01 декабря 2019
Мама может оставаться занятой. YouClever решает! (с) 🙂 Если серьезно, то очень приятно читать такие комментарии, Ниважна. Для того этот учебник и писали, чтобы было понятно. Удачи тебе!
Аня
03 февраля 2020
Есть у вас что нибудь на тему ЛИНЕЙНЫХ УРАВНЕНИЙ (неравенств,функций)?))) Кстати спасибо за прошлую тему.)))
Александр (админ)
04 февраля 2020
Аня, конечно есть. Вот здесь оглавление, всего, что есть. Там и линейные уравнения и неравенства и функции. https://youclever.org/book/ А что за прошлая тема? )))
brff
20 мая 2020
а как быть с примером 25a-ab^2? По статье ничего не понял..
Фаридун
11 июня 2020
Общий множитель у нас а . Значит выносим из-за скобки , тогда получим a(25-b^2)
Александр (админ)
11 июня 2020
Спасибо, Фаридун
Фаридун
11 июня 2020
Разложите на множители : a^3+b^3+c^3-3abc
Алексей Шевчук
11 июня 2020
Фаридун, классная задача! Рассмотрите (a+b+c)^3. Если раскрыть скобки, мы там увидим a^3+b^3+c^3+…+6abc (вместо троеточия ещё куча слагаемых). Вычтем и прибавим 3abc, тогда получим: (a+b+c)^3 = a^3+b^3+c^3+…+9abc — 3abc. Это значит, что можно выразить искомое выражение (обозначим его за X): X = (a+b+c)^3 — … — 9abc. В получившемся выражении можно 9abc разбить на 3 слагаемых 3abc, и тогда получится разлжить на множители группировкой. Напишите, что получилось?
Ангелина
23 июня 2020
Здравствуйте! Пожалуйста, помогите с разложением выражения на множители. 4+0,25х^2-2х. Я решила как (2-0,5х)^2, но гдз говорит (0,5х-2)^2. Не понимаю, это одно и тоже, или я что-то не понимаю… Спасибо большое заранее
Алексей Шевчук
23 июня 2020
Ангелина, это одно и то же, всё правильно.
Здравствуйте, помогите, пожалуйста, разложить на множители x⁵ — 32
Елена, (x-2)(x^4+2x^3+4x^2+8x+16)