Тригонометрическая окружность
Привет! Сегодня я научу тебя делать универсальную шпаргалку по тригонометрии, которая называется тригонометрическая окружность.
Ты научишься:
- Обобщению всех тригонометрических функций на произвольные (абсолютно произвольные!) положительные и отрицательные углы;
- Градусной и радианной мере углов, связи между ними;
- Знакам тригонометрических функций для всех углов по четвертям;
- Способу вычисления значений тригонометрических функций (не нужно помнить никаких таблиц!)
Самое главное?
Если ты поймешь, что такое тригонометрическая окружность, то вся дальнейшая тригонометрия тебе покажется не более чем легкой прогулкой.
Открою секрет: с помощью окружности даже можно решать уравнения и неравенства!
Итак, давай приступим.
Тригонометрическая окружность — коротко о главном
Главный инструмент тригонометрии — это тригонометрическая окружность, она позволяет измерять углы, находить их синусы, косинусы и прочее.
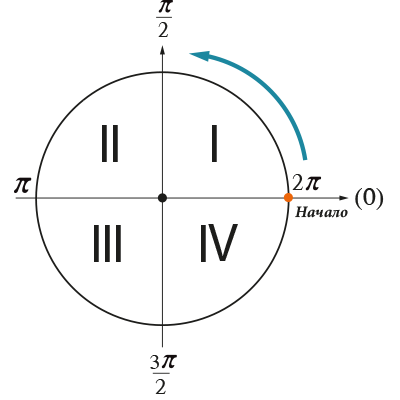
Есть два способа измерять углы:
- Через градусы
- Через радианы
\( \displaystyle 180{}^\circ =\pi ~рад.\)
Чтобы пересчитать угол из градусов в радианы, нужно применить вот такую незамысловатую формулу:
\( \displaystyle P~рад.=\frac{\alpha {}^\circ \cdot \pi }{180}\)
И наоборот: от радиан к градусам:
\( \displaystyle y=sin\ \alpha \)
\( \displaystyle x=cos\ \alpha \)
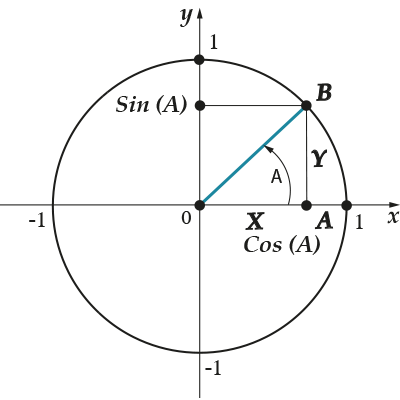
Чтобы найти синус и косинус угла, нужно:
- Провести единичную окружность с центром, совпадающим с вершиной угла.
- Найти точку пересечения этого угла с окружностью.
- Её «иксовая» координата – это косинус искомого угла.
- Её «игрековая» координата – это синус искомого угла.
Формулы приведения:
Это формулы, позволяющие упростить сложные выражения тригонометрической функции.
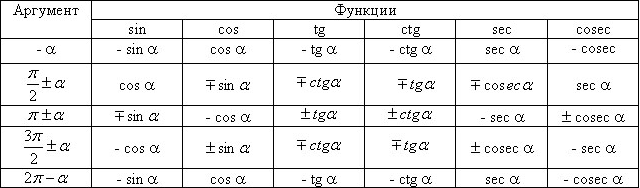
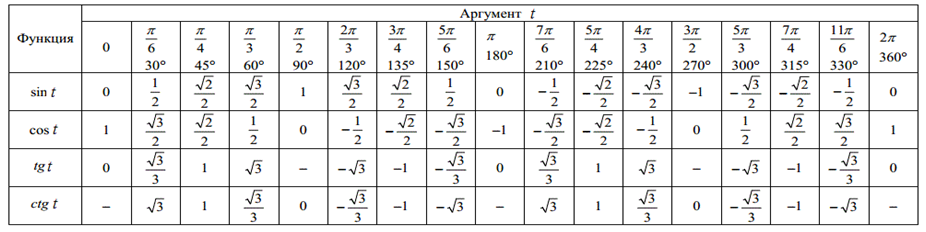
Эти формулы помогут тебе не запоминать вот такую таблицу:
Что нужно повторить
Вот, что тебе нужно повторить, если ты это забыл:
- Что такое синус, косинус, тангенс, котангенс (острого угла в прямоугольном треугольнике);
- Теорема Пифагора (куда уж без нее!);
- Система координат.
Вот картинка, которая кратко напомнит тебе, что такое эти синусы, косинусы и т. д.
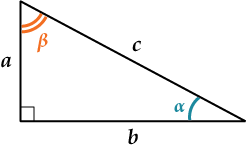
Также давай вспомним основные соотношения между синусами, косинусами, тангенсами одного и второго острых углов прямоугольного треугольника:
- \( \displaystyle \alpha +\beta =90{}^\circ \)
- \( \displaystyle cos\ \alpha =sin\ \beta \)
- \( \displaystyle sin\ \alpha =cos\ \beta \)
- \( \displaystyle tg\ \alpha =ctg\ \beta \)
То есть:
Синус одного острого угла равен косинусу другого (и наоборот), тангенс одного острого угла равен котангенсу другого (и наоборот).
Данные утверждения были доказаны в других статьях. Мы же здесь с тобой уже будем почивать на лаврах, пожиная эти плоды.
Построение тригонометрической окружности
А теперь сделай вот что: возьми-ка в руки циркуль и нарисуй любую (самую любую, но лучше достаточно немаленькую) окружность.
Получилось?

Ну да ладно, задачка не самая сложная. Так, ты не потерял ту точку, в которой у тебя был центр (куда ты прикладывал острую ножку циркуля)? Я вот у себя потерял, растяпа! Ну ладно, найду!
А что пока делать тебе?
А вот что: проведи через эту точку две линии, которые пересекаются «прямым крестиком», то есть под прямым углом. И пусть их точка пересечения – это центр (который ты не потерял!) окружности.
Нарисовал? У меня получилось что-то вроде вот этого.

Правда я чуть-чуть поторопился и сразу «обозвал» эти прямые \( \displaystyle x\) и \( \displaystyle y\) и точку пересечения через \( \displaystyle O\).
А что такое в таком случае \( \displaystyle R\)?
Это радиус нашей окружности.
Как называлась наша тема? Единичная окружность.
Тогда будем считать ( но не будем так рисовать!), что \( \displaystyle R=1\ \).
А рисовать мы так не будем, потому что на такой крошечной картинке ты ничего не разберешь! Ты же понимаешь, что когда инженеры проектируют самолеты, скажем, они не рисуют его в натуральную величину?
Так и мы не будем рисовать единичную окружность в самом деле единичной. Это нам нужно исключительно для удобства.
Теперь отмечаем: \( \displaystyle OR=1\). Что же мы с тобой на самом деле сделали? А вот что:
Мы поместили нашу окружность в систему координат \( \displaystyle \mathbf{X0Y}\), сделав центр окружности началом координат!
Это позволит изучать свойства такой окружности уже не с геометрической, а с математической точки зрения. Этот подход был придуман хитрым математиком и философом Рене Декартом еще в 17 веке!
Перегнать фигуру в цифры, каково, а?
Но допустим, мы поместили нашу окружность в координаты. В скольких точках она пересекается с осями системы координат?
В четырех. Вот они:
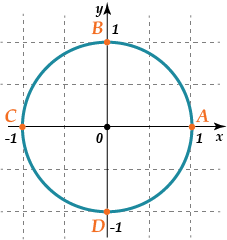
Эти точки \( \displaystyle \left( A;\ B;\ C;\ D \right)\) имеют координаты:
\( \displaystyle A\left( 1,0 \right)\); \( \displaystyle B\left( 0,1 \right)\); \( \displaystyle C\left( -1;0 \right)\); \( \displaystyle D\left( 0;-1 \right)\).
Теперь вспомни, как называются области, на которые этот «координатный крестик» делит всю плоскость?
Они называются координатные четверти.
Тогда посмотри на рисунок. Наша окружность тоже оказалась разрезанной на 4 равные дольки. Давай пронумеруем каждую из этих долек против часовой стрелки:
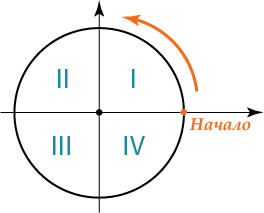
Ты уже можешь догадаться, как называются эти самые дольки:
1 четверть, 2 четверть, 3 четверть, 4 четверть
(Прямо как четверти в школе!)
Углы на тригонометрической окружности
Теперь давай сделаем еще вот что. Снова посмотрим на предыдущую картинку.
Чему на ней равен \( \displaystyle \angle AOB\)?
Он равен \( \displaystyle 90{}^\circ \).
Также, как и \( \displaystyle \angle BOC\), как и угол \( \displaystyle \angle COD\), и угол \( \displaystyle \angle DOA\).
\( \displaystyle \angle \text{AOB}=\angle \text{BOC}=\angle \text{COD}=\angle \text{DOA}=90{}^\circ \)
Тогда чему равна их сумма?
Она равна \( \displaystyle 360{}^\circ \).
Вместе же эти 4 угла составляют всю окружность целиком!
Градусная мера окружности равна \( \displaystyle 360{}^\circ \)!
\( \displaystyle \angle A\text{OC}=\angle \text{AOB}+\angle \text{BOC}=180{}^\circ \)
Что еще можно вытянуть? А вот что:
\( \displaystyle \angle A\text{OD}=\angle \text{AOB}+\angle \text{BOC}+\angle \text{COD}=270{}^\circ \)
Отметим эти значения также на нашей окружности:
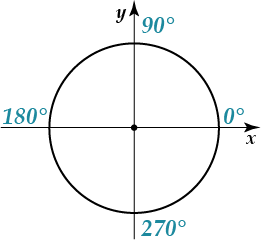
Однако, ты нередко можешь увидеть и вот такую картинку:
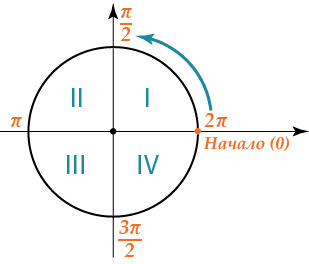
где вместо привычных нам градусов появляются некие буковки «пи» \( \displaystyle \pi \) с цифрами.
В чем же тут дело, кто прав и кто виноват?
Ну так вот, кто прав, кто виноват, решать, увы, не нам. Но чтобы «воз не был поныне там», нам нужно уделить этому моменту пару минут времени.
В самом деле, есть два способа измерять углы:
- Через градусы
- Через радианы
Как измерять углы через градусы мы все знаем. Это нам привычно. Однако в некоторых случаях их измеряют по-другому (как в градуснике есть несколько шкал: цельсий, кельвин, фаренгейт и т. д.), а именно: через радианы.
Для того, чтобы перейти от одной формы записи к другой, используется вот такое основное соотношение:
\( \displaystyle 180{}^\circ =\pi ~рад.\)
И все, больше знать ничего не надо!
По пропорции ты легко получишь, что для того, чтобы пересчитать угол из градусов в радианы, нужно применить вот такую незамысловатую формулу:
\( \displaystyle P~рад.=\frac{\alpha {}^\circ \cdot \pi }{180}\)
И наоборот: от радиан к градусам:
\( \displaystyle \alpha {}^\circ =\frac{P~рад.\cdot 180}{\pi }\)
Ты должен уметь ориентироваться и в той, и в другой форме записи.
Потренируйся на следующих примерах:
- Перевести угол в \( \displaystyle 30\) градусов в радианы;
- Перевести угол \( \displaystyle \frac{\pi }{4}\) радиан в градусы;
- Перевести угол в \( \displaystyle 60\) градусов в радианы;
- Перевести угол в \( \displaystyle \frac{\pi }{2}\) радиан в градусы;
- Перевести угол в \( \displaystyle 120\) градусов в радианы;
- Перевести угол в \( \displaystyle \frac{3\pi }{4}\) радиан в градусы;
- Перевести угол в \( \displaystyle 150\) градусов в радианы.
Я сделаю только первые два, а остальные реши сам!
- \( P~рад.=\frac{30\cdot \pi }{180}=\frac{\pi }{6}\), тогда угол в \( \displaystyle 30\) градусов равен углу в \( \displaystyle \frac{\pi }{6}\) радиан;
- \( \alpha {}^\circ =\frac{\frac{\pi }{4}\cdot 180}{\pi }=\frac{45\pi }{\pi }=45{}^\circ \), тогда угол в \( \displaystyle \frac{\pi }{4}\) радиан равен углу в \( \displaystyle 45\) градусов.
Все очень просто, не так ли? Остальные значения ты можешь найти в следующей таблице:
| \( \displaystyle 0{}^\circ \) | \( \displaystyle 30{}^\circ \) | \( \displaystyle 45{}^\circ \) | \( \displaystyle 60{}^\circ \) | \( \displaystyle 90{}^\circ \) | \( \displaystyle 120{}^\circ \) | \( \displaystyle 135{}^\circ \) | \( \displaystyle 150{}^\circ \) | \( \displaystyle 180{}^\circ \) |
| \( \displaystyle 0\) | \( \displaystyle \frac{\pi }{6}\) | \( \displaystyle \frac{\pi }{4}\) | \( \displaystyle \frac{\pi }{3}\) | \( \displaystyle \frac{\pi }{2}\) | \( \displaystyle \frac{2\pi }{3}\) | \( \displaystyle \frac{3\pi }{4}\) | \( \displaystyle \frac{5\pi }{6}\) | \( \displaystyle \pi \) |
| \( \displaystyle 210{}^\circ \) | \( \displaystyle 225{}^\circ \) | \( \displaystyle 240{}^\circ \) | \( \displaystyle 270{}^\circ \) | \( \displaystyle 300{}^\circ \) | \( \displaystyle 315{}^\circ \) | \( \displaystyle 330{}^\circ \) | \( \displaystyle 360{}^\circ \) |
| \( \displaystyle \frac{7\pi }{6}\) | \( \displaystyle \frac{5\pi }{4}\) | \( \displaystyle \frac{4\pi }{3}\) | \( \displaystyle \frac{3\pi }{2}\) | \( \displaystyle \frac{5\pi }{3}\) | \( \displaystyle \frac{7\pi }{4}\) | \( \displaystyle \frac{11\pi }{6}\) | \( \displaystyle 2\pi \) |
Так что впредь не удивляйся, когда ты увидишь вместо привычных градусов углы в радианах. Теперь ты знаешь, что это такое, и с чем его едят!
Подведем предварительные, но очень важные итоги:
- В первой четверти лежат углы от \( \displaystyle 0\) до \( \displaystyle 90\) градусов (от \( \displaystyle 0\) до \( \displaystyle \frac{\pi }{2}\) радиан);
- Во второй четверти лежат углы от \( \displaystyle 90\) до \( \displaystyle 180\) градусов (от \( \displaystyle \frac{\pi }{2}\) до \( \displaystyle \pi \) радиан);
- В третьей четверти лежат углы от \( \displaystyle 180\) до \( \displaystyle 270\) градусов (от \( \displaystyle \pi \) до \( \displaystyle \frac{3\pi }{2}\) радиан);
- В четвертой четверти лежат углы от \( \displaystyle 270\) до \( \displaystyle 360\) градусов (от \( \displaystyle \frac{3\pi }{2}\) до \( \displaystyle 2\pi \) радиан).
Синус, косинус, тангенс и котангенс на тригонометрической окружности
Но мы с тобой и так слишком увлеклись. Ты давно уже, наверное, заждался обещанных синусов и косинусов на тригонометрической окружности. Не смею более отвлекаться!
Давай сделаем вот что: совместим два знакомых нам объекта: тригонометрическую окружность (пока в том виде, в котором она у нас есть) и прямоугольный треугольник.
Что нам нужно, чтобы наш треугольник «целиком влез» в окружность?
Его гипотенуза должна быть не более единицы. Пусть же она у нас в точности будет равна единице.
Совместим мы их вот так:

Я нарисовал прямоугольный треугольник с центром в начале координат и гипотенузой равной \( 1\). Это так потому, что окружность-то у меня единичная!
Тогда по определению синуса и косинуса:
- \( sin\ \alpha =\frac{AB}{OB}=\frac{AB}{1}=AB\)
- \( cos\ \alpha =\frac{OA}{OB}=\frac{OA}{1}=OA\)
А что же такое отрезки \( OA\) и \( OB\)? Чему равны их длины?
Смотри, сейчас будет самое главное: мы взяли угол \( \alpha \) и провели луч, соединяющий этот угол с точкой на окружности.
Обозначим эту точку через \( B\). Пусть \( B\) имеет координаты \( B\left( x,y \right)\).
Тогда длина отрезка \( OA\) равна \( x\), а длина отрезка \( AB\)–равна \( y\).
Но мы с тобой помним, что \( sin\ \alpha =AB\), \( cos\ \alpha =OA\), тогда:
- \( y=sin\ \alpha \)
- \( x=cos\ \alpha \)

Ух ты! Это надо еще раз обдумать, что же мы такое получили.
Давай проговорим еще раз: мы выбрали некоторый угол \( \alpha \) и хотим найти его синус и косинус.
Что мы делаем?
- Проводим единичную окружность с центром, совпадающим с вершиной угла;
- Ищем точку пересечения нашего угла с окружностью;
- Её «иксовая» координата – это косинус нашего угла;
- Её «игрековая» координата – это синус нашего угла.
Вот и все! Теперь синус и косинус искать стало намного проще! Допустим, мы хотим найти синус, косинус \( 30\) градусов.
Отмечаем \( 30\) градусов на окружности и «достраиваем» этот угол до треугольника (как показано на рисунке выше).
Как найти \( x\) и \( y\)?
Да очень просто: в прямоугольном треугольнике катет, лежащий против угла в \( 30\) градусов равен половине гипотенузы (это известный факт из геометрии 7 класса).
Так как гипотенуза равна \( 1\), то противолежащий ей катет равен \( 0,5\), откуда:
\( sin\ 30{}^\circ =0,5\)
Что касается косинуса: для этого нам потребуется заметить, что выполняется тривиальное утверждение (основное тригонометрическое тождество):
\( si{{n}^{2}}\alpha +co{{s}^{2}}\alpha =1\)
Как ты думаешь, откуда оно берется? Да это же пресловутая теорема Пифагора!
Наши катеты в треугольничке равны \( x\) и \( y\), которые в свою очередь совпадают с \( cos\ \alpha \) и \( sin\ \alpha \). Гипотенуза в треугольнике равна \( 1\).
Тогда:
\( {{x}^{2}}+{{y}^{2}}=1\) или, что то же самое,
\( si{{n}^{2}}\alpha +co{{s}^{2}}\alpha =1\)
Эта формула позволит по известному синусу вычислить неизвестный косинус и наоборот.
В частности, если:
\( si{{n}^{2}}30{}^\circ +co{{s}^{2}}30{}^\circ =1\) и \( sin\ 30{}^\circ =0,5\), то
\( \frac{1}{4}+co{{s}^{2}}30{}^\circ =1\)
\( \displaystyle co{{s}^{2}}30{}^\circ =\frac{3}{4}\)
\( \displaystyle cos\ 30{}^\circ =\pm \sqrt{\frac{3}{4}}=\pm \frac{\sqrt{3}}{2}\)
Определение знака синуса, косинуса, тангенса и котангенса
Вообще, этот вопрос заслуживает особого внимания, но здесь все просто: у угла \( \displaystyle 30\) градусов и синус и косинус положительны (смотри рисунок), тогда берем знак «плюс».
\( \displaystyle cos\ 30{}^\circ =\frac{\sqrt{3}}{2}\)
Теперь попробуй на основе вышеизложенного найти синус и косинус углов: \( \displaystyle 60{}^\circ \) и \( \displaystyle 45{}^\circ \)
Можно схитрить: в частности для угла в \( \displaystyle 60{}^\circ \) градусов. Так как если один угол прямоугольного треугольника равен \( \displaystyle 60{}^\circ \) градусам, то второй – \( \displaystyle 30{}^\circ \) градусам. Теперь вступают в силу знакомые тебе формулы:
\( \displaystyle sin\ 30{}^\circ =cos\ 60{}^\circ \)
\( \displaystyle sin\ 60{}^\circ =cos\ 30{}^\circ \)
Тогда так как \( \displaystyle sin\ 30{}^\circ =0,5\), то и \( \displaystyle cos\ 60{}^\circ =0,5\). Так как \( \displaystyle cos\ 30{}^\circ =\frac{\sqrt{3}}{2}\), то и \( \displaystyle sin\ 60{}^\circ =\frac{\sqrt{3}}{2}\).
C \( \displaystyle 45\) градусами все еще проще: так если один из углов прямоугольного треугольника равен \( \displaystyle 45\) градусам, то и другой тоже равен \( \displaystyle 45\) градусам, а значит такой треугольник равнобедренный.
Значит, его катеты равны. А значит равны его синус и косинус.
Тогда:
\( \displaystyle si{{n}^{2}}45{}^\circ +co{{s}^{2}}45{}^\circ =2si{{n}^{2}}45{}^\circ =1\)
\( \displaystyle si{{n}^{2}}45{}^\circ =co{{s}^{2}}45{}^\circ =1/2\)
Откуда: \( \displaystyle sin 45{}^\circ =cos 45{}^\circ =\sqrt{1/2}=\frac{\sqrt{2}}{2}\)
Теперь найди сам по новому определению (через икс и игрек!) синус и косинус углов в \( \displaystyle 0\) градусов и \( \displaystyle 90\) градусов. Здесь уже никакие треугольники нарисовать не получится! Уж слишком они будут плоские!
У тебя должно было получиться:
\( \displaystyle sin\ 0{}^\circ =0\), \( \displaystyle cos\ 0{}^\circ =1\), \( \displaystyle sin\ 90{}^\circ =1\), \( \displaystyle cos\ 90{}^\circ =0\).
Тангенс и котангенс ты можешь отыскать самостоятельно по формулам:
\( \displaystyle \text{t}g\ \alpha =\frac{\sin \alpha }{\cos \alpha }\), \( \displaystyle ctg\ \alpha =\frac{cos\ \alpha }{sin\ \alpha }\)
Обрати внимание, что на ноль делить нельзя!!
Теперь все полученные числа можно свести в таблицу:
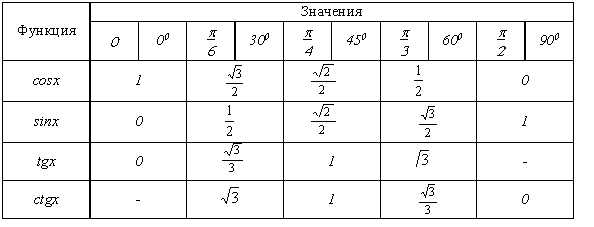
Здесь приведены значения синуса, косинуса, тангенса и котангенса углов I четверти.
Для удобства углы приведены как в градусах, так и в радианах (но ты-то теперь знаешь связь между ними!). Обрати внимание на 2 прочерка в таблице: а именно у котангенса нуля и тангенса \( \displaystyle 90\) градусов. Это неспроста!
В частности:
\( \displaystyle ctg 0=\frac{\cos 0}{\sin 0}=\frac{1}{0}=?????\)
Поэтому мы с тобой будем считать, что тангенс \( \displaystyle 90\) градусов и котангенс нуля просто-напросто не определены!
Теперь давай обобщим понятие синус и косинус на совсем произвольный угол. Я рассмотрю здесь два случая:
- Угол лежит в пределах от \( \displaystyle 0\) до \( \displaystyle 360\) градусов;
- Угол больше \( \displaystyle 360\) градусов.
Честно говоря, я скривил немного душой, говоря про «совсем все» углы. Они бывают также и отрицательными! Но этот случай мы с тобой рассмотрим чуть позже. Вначале остановимся на первом случае.
Если угол лежит в 1 четверти – то тут все понятно, мы этот случай уже рассмотрели и даже таблицы нарисовали.
Теперь же пусть наш угол больше \( \displaystyle 90\) градусов и не больше чем \( \displaystyle 360\).
Это значит, что он расположен либо во 2, либо в 3 или же в 4 четверти.
Как мы поступаем? Да точно так же!
Давай рассмотрим вместо вот такого случая…
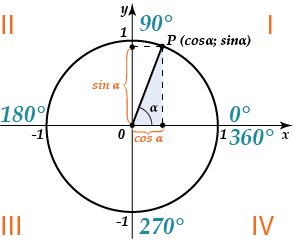
…вот такой:

То есть рассмотрим угол \( \displaystyle \alpha \), лежащий во второй четверти. Что мы можем сказать про него?
У точки \( \displaystyle {{M}_{1}}\), которая является точкой пересечения луча и окружности по-прежнему имеет 2 координаты (ничего сверхъестественного, правда?). Это координаты \( \displaystyle {{x}_{1}}\) и \( \displaystyle {{y}_{1}}\).
Причем первая координата отрицательная, а вторая – положительная! Это значит, что у углов второй четверти косинус отрицателен, а синус – положителен!
Удивительно, правда? До этого мы еще ни разу не сталкивались с отрицательным косинусом.
Да и в принципе этого не могло быть, когда мы рассматривали тригонометрические функции как отношения сторон треугольника.
Кстати, подумай, у каких углов косинус равен \( \displaystyle -1\)? А у каких \( \displaystyle -1\) равен синус?
Аналогично можно рассмотреть углы во всех остальных четвертях. Я лишь напомню, что угол отсчитывается против часовой стрелки! (так, как это показано на последнем рисунке!).
Конечно, можно и отсчитывать в другую сторону, но вот подход к таким углам будет уже несколько другой.
Исходя из приведенных выше рассуждений, можно расставить знаки у синуса, косинуса, тангенса (как синус деленный на косинус) и котангенса (как косинус деленный на синус) для всех четырех четвертей.
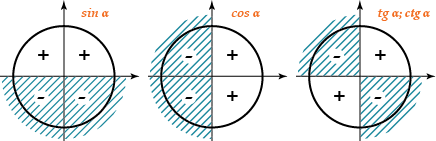
Но еще раз повторюсь, нет смысла запоминать этот рисунок. Все, что тебе нужно знать:
Синус – это игрек. Косинус – это икс. Тангенс – это синус деленный на косинус. Котангенс – это косинус деленный на синус.
Задачи на тренировку
Выяснить, какой знак имеют следующие величины:
Задача №1. \( \displaystyle sin\ 225{}^\circ ,\ tg\ 100{}^\circ ,\ \cos \ 300{}^\circ \);
Задача №2. \( \displaystyle sin\ \frac{2\pi }{3},\ \cos \ \frac{11\pi }{6},\ tg\frac{7\pi }{4}\).
Проверим?
Теперь я хотел бы очень кратко остановиться вот еще на каком моменте. Давай снова вспомним основное тригонометрическое тождество.
\( \displaystyle si{{n}^{2}}\alpha +co{{s}^{2}}\alpha =1\)
Как я уже говорил, из него мы можем выразить синус через косинус или наоборот:
\( \displaystyle sin\ \alpha =\pm \sqrt{1-co{{s}^{2}}\alpha }\)
\( \displaystyle cos\ \alpha =\pm \sqrt{1-si{{n}^{2}}\alpha }\)
На выбор знака же будет влиять только та четверть, в которой находится наш угол альфа. На последние две формулы существует масса задач в ЕГЭ, например, вот таких:
Задача №3
Найдите \( \displaystyle 3cos\alpha \), если \( \displaystyle sin\alpha =-\frac{2\sqrt{2}}{3}\) и \( \displaystyle \alpha \in \left( \frac{3\pi }{2};2\pi \right)\).
На самом деле, это задача на четверть! Смотри, как она решается:
Углы больше 360 градусов
А как быть с углами, большими чем \( \displaystyle 360\) градусов?
Возьму я, скажем, угол в \( \displaystyle 30\) градусов (\( \displaystyle \frac{\pi }{6}\) радиан) и пойду от него против часовой стрелки…
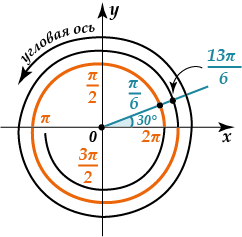
На рисунке я нарисовал спираль, но ты-то понимаешь, что на самом деле у нас нет никакой спирали: у нас есть только окружность.
Так куда же мы попадем, если стартуем от определенного угла и пройдем полностью весь круг (\( \displaystyle 360\) градусов или \( \displaystyle 2\pi \) радиан)?
Куда мы придем? А придем мы в тот же самый угол!
Это же, конечно, справедливо и для любого другого угла:
Взяв произвольный угол \( \displaystyle \alpha \) и пройдя полностью всю окружность, мы вернемся в тот же самый угол \( \displaystyle \alpha \).
Что же нам это даст? А вот что: если \( \displaystyle sin\ \alpha =y,~cos\ \alpha =x\), то
\( \displaystyle \sin \left( \alpha +2\pi k \right)=y\), \( \displaystyle \cos \left( \alpha +2\pi k \right)=x\), откуда окончательно получим:
\( \displaystyle \sin \left( \alpha +2\pi k \right)=sin\alpha \) \( \displaystyle \cos \left( \alpha +2\pi k \right)=cos\alpha \)Для любого целого \( \displaystyle k\). Это значит, что синус и косинус являются периодическими функциями с периодом \( \displaystyle 2\pi \).
Таким образом, нет никакой проблемы в том, чтобы найти знак теперь уже произвольного угла: нам достаточно отбросить все «целые круги», которые умещаются в нашем угле и выяснить, в какой четверти лежит оставшийся угол.
Например, найти знак:
- \( \displaystyle \text{sin}1000{}^\circ \),
- \( \displaystyle \text{cos}\ 605{}^\circ \),
- \( \displaystyle \text{cos}\frac{16\pi }{7}\),
- \( \displaystyle \text{sin}\frac{19\pi }{4}\).
Проверяем:
Промежуточный итог
Итак, ты понял что такое тригонометрическая окружность и для чего она нужна.
Но у нас осталось еще очень много вопросов:
- А что такое отрицательные углы?
- Как вычислять значения тригонометрических функций в этих углах?
- Как по известным значениям тригонометрических функций 1 четверти искать значения функций в других четвертях (неужто надо зубрить таблицу?!)
- Как с помощью круга упрощать решения тригонометрических уравнений?
Чтобы узнать ответы на них, читай далее!
Отрицательные углы
Отрицательные углы в тригонометрии откладываются на тригонометрическом круге вниз от начала, по направлению движения часовой стрелки:
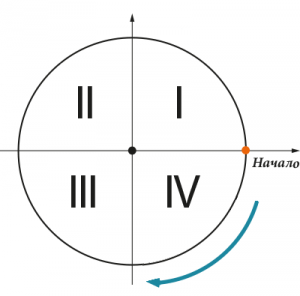
Давай вспомним, как мы до этого откладывали углы на тригонометрической окружности.
Мы шли от положительного направления оси \( \displaystyle Ox\) против часовой стрелки:
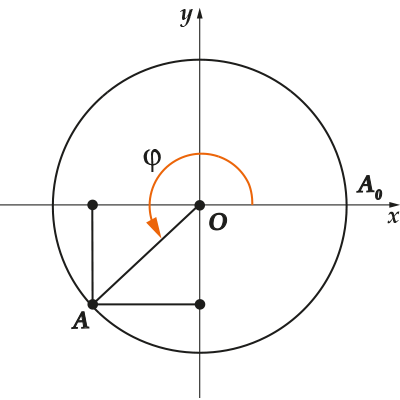
Тогда на нашем рисунке построен угол, равный \( \displaystyle 180+45=225{}^\circ \). Аналогичным образом мы строили все углы.
Однако ничего нам не запрещает идти от положительного направления оси \( \displaystyle Ox\) по часовой стрелке.
Мы будем тоже получать различные углы, но они будут уже отрицательными:
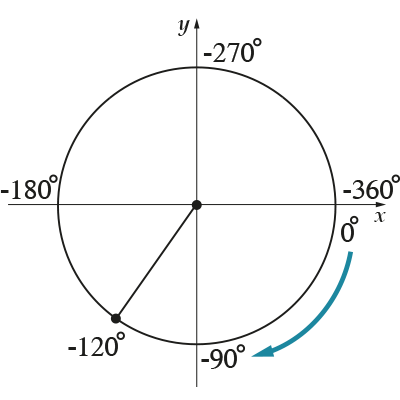
А следующей картинке изображено два угла, равные по абсолютной величине (если не знаешь, что это такое, читай здесь про «Модуль числа»), но противоположные по знаку:
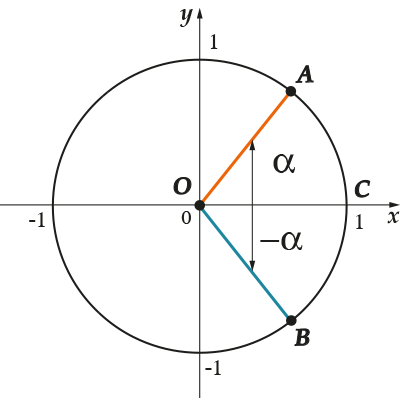
В целом правило можно сформулировать вот так:
- Идем против часовой стрелки – получаем положительные углы
- Идем по часовой стрелке – получаем отрицательные углы
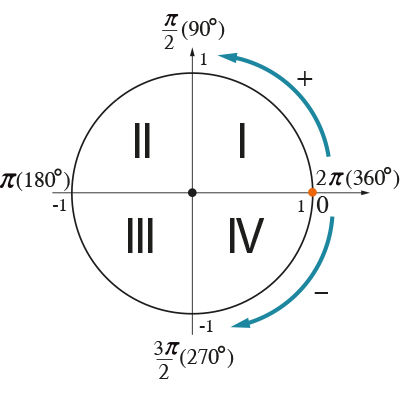
Схематично правило изображено вот на этом рисунке:
Ты мог бы задать мне вполне резонный вопрос: ну углы нам нужны для того, чтобы измерять у них значения синуса, косинуса, тангенса и котангенса.
Так есть ли разница, когда у нас угол положительный, а когда – отрицательный? Я отвечу тебе: как правило есть.
Однако ты всегда можешь свести вычисление тригонометрической функции от отрицательного угла к вычислению функции в угле положительном.
Посмотри на следующую картинку:
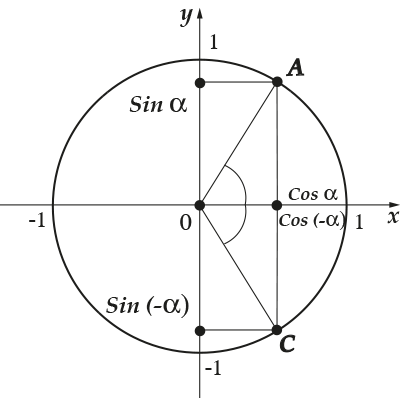
Я построил два угла, они равны по абсолютному значению, но имеют противоположный знак. Отметим для каждого из углов его синус и косинус на осях.
Что мы с тобой видим? А вот что:
Синусы у углов \( \displaystyle \alpha \) и \( \displaystyle -\alpha \) противоположны по знаку!
Тогда если \( \displaystyle \text{sin}\ \text{ }\!\!\alpha\!\!\text{ }=\text{y}\),
то \( \displaystyle \sin \left( -\text{ }\!\!\alpha\!\!\text{ } \right)=-\text{y}\)
\( \displaystyle \sin \left( -\text{ }\!\!\alpha\!\!\text{ } \right)=-\text{sin}\ \text{ }\!\!\alpha\!\!\text{ }\).
Косинусы у углов \( \displaystyle \alpha \) и \( \displaystyle -\alpha \) совпадают!
Тогда если \( \displaystyle \text{cos}\ \text{ }\!\!\alpha\!\!\text{ }=\text{x}\),
то и \( \displaystyle \cos \left( -\text{ }\!\!\alpha\!\!\text{ } \right)=\text{x}\)
\( \displaystyle \cos \left( -\text{ }\!\!\alpha\!\!\text{ } \right)=\text{cos}\ \text{ }\!\!\alpha\!\!\text{ }\)
Так как \( \displaystyle \text{tg}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)=\frac{\text{sin}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)}{\text{cos}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)}=\frac{-\text{sin}\left( \text{ }\!\!\alpha\!\!\text{ } \right)}{\text{cos}\left( \text{ }\!\!\alpha\!\!\text{ } \right)}\), то:
\( \displaystyle \text{tg}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)=-\text{tg }\!\!\alpha\!\!\text{ }\)
Так как \( \displaystyle \text{ctg}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)=\frac{\text{cos}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)}{\text{sin}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)}=\frac{\text{cos}\left( \text{ }\!\!\alpha\!\!\text{ } \right)}{-\text{sin}\left( \text{ }\!\!\alpha\!\!\text{ } \right)}\), то:
\( \displaystyle \text{ctg}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)=-\text{ctg}\ \text{ }\!\!\alpha\!\!\text{ }\)
Таким образом, мы всегда можем избавиться от отрицательного знака внутри любой тригонометрической функции: либо просто уничтожив его, как у косинуса, либо поставив его перед функцией, как у синуса, тангенса и котангенса.
Кстати, вспомни-ка, как называется функция \( \displaystyle f(x)\), у которой для любого допустимого \( \displaystyle x\) выполняется:\( \displaystyle f(-x)=-f(x)\)?
Такая функция называется нечетной.
А если же для любого допустимого \( \displaystyle x\) выполняется: \( \displaystyle f(-x)=f(x)\)? То в таком случае функция называется четной.
Таким образом, мы с тобой только что показали, что:
Синус, тангенс и котангенс – нечетные функции, а косинус – четная.
Таким образом, как ты понимаешь, нет никакой разницы, ищем ли мы синус от положительного угла или отрицательного: справиться с минусом очень просто. Так что нам не нужны таблицы отдельно для отрицательных углов.
С другой стороны, согласись, было бы очень удобно зная только тригонометрические функции углов первой четверти, уметь вычислять аналогичные функции и для остальных четвертей.
Можно ли это сделать? Конечно, можно!
У тебя есть по крайней мере 2 пути: первый – строить треугольник и применять теорему Пифагора (так мы с тобой и отыскали значения тригонометрических функций для основных углов первой четверти)
Второй – запомнив значения функций для углов в первой четверти и некое несложное правило, уметь вычислять тригонометрические функции для всех остальных четвертей.
Второй способ избавит тебя от долгой возни с треугольниками и с Пифагором, поэтому мне он видится более перспективным:
Итак, данный способ (или правило) называется формулами приведения.
Формулы приведения
Грубо говоря, эти формулы помогут тебе не запоминать вот такую таблицу (она между прочим содержит 98 чисел!):

…если ты помнишь вот эту (всего на 20 чисел):
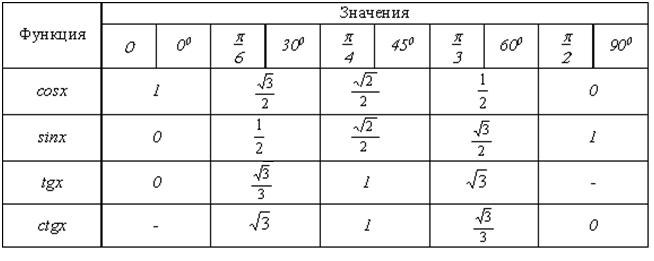
То есть ты сможешь не забивать себе голову совершенно ненужными 78 числами! Пусть, например, нам нужно вычислить \( \displaystyle \text{sin}\ 855{}^\circ \). Ясно, что в маленькой таблице такого нет. Что же нам делать? А вот что:
Во-первых, нам понадобятся следующие знания:
Синус и косинус имеют период \( \displaystyle 2\pi \) (\( \displaystyle 360\) градусов)
То есть
\( \displaystyle sin\left( 2\pi k+x \right)=sin x\)
\( \displaystyle cos\left( 2\pi k+x \right)=cos x\)
\( \displaystyle tg\left( \pi k+x \right)=tg x\)Тангенс (котангенс) имеют период \( \displaystyle \pi \) (\( \displaystyle 180\) градусов)
\( \displaystyle ctg\left( \pi k+x \right)=ctg x\)
\( \displaystyle k\) – любое целое число
Синус и тангенс – функции нечетные, а косинус – четная:
\( \displaystyle sin\left( -x \right)=-sin x\)
\( \displaystyle tg\left( -x \right)=-tg\left( x \right)\)
\( \displaystyle cos\left( -x \right)=cos\left( x \right)\)
Первое утверждение мы уже доказали с тобой, а справедливость второго установили совсем недавно.
Непосредственно правило приведения выглядит вот так:
Если мы вычисляем значение тригонометрической функции от отрицательного угла – делаем его положительным при помощи группы формул о четности.
Например:
\( \displaystyle sin\left( -855{}^\circ \right)=-sin855{}^\circ\),
\( \displaystyle cos\left( -855{}^\circ \right)=cos855{}^\circ\).
Отбрасываем для синуса и косинуса его периоды: \( \displaystyle 2\pi k\) (по \( \displaystyle 360\) градусов), а для тангенса – \( \displaystyle \pi k\) (\( \displaystyle 180\) градусов).
Например:
\( \displaystyle sin\ 855{}^\circ =sin\left( 2\cdot 360{}^\circ +135{}^\circ \right)=sin\ 135{}^\circ \)\( \displaystyle tg\ 225{}^\circ =tg\left( 180{}^\circ +45{}^\circ \right)=tg\ 45{}^\circ \)
Если оставшийся «уголок» меньше \( \displaystyle 90\) градусов, то задача решена: ищем его в «малой таблице».
Иначе ищем, в какой четверти лежит наш угол \( \displaystyle \alpha \): это будет 2, 3 или 4 четверть. Смотрим, какой знак имеет искомая функция в четверти. Запомнили этот знак!!!
Представляем угол \( \displaystyle \alpha \)в одной из следующих форм:
- \( \displaystyle \alpha =90+\beta \) (если во второй четверти)
- \( \displaystyle \alpha =180-\beta \) (если во второй четверти)
- \( \displaystyle \alpha =180+\beta \) (если в третьей четверти)
- \( \displaystyle \alpha =270-\beta \) (если в третьей четверти)
- \( \displaystyle \alpha =270+\beta \) (если в четвертой четверти)
- \( \displaystyle \alpha =360-\beta \) (если в четвертой четверти)
…так, чтобы оставшийся угол \( \displaystyle \beta \) был больше нуля и меньше \( \displaystyle 90\) градусов.
Например:
\( \displaystyle 135{}^\circ =180{}^\circ -45{}^\circ \)
\( \displaystyle 135{}^\circ =90{}^\circ +45{}^\circ \)
\( \displaystyle 315{}^\circ =270{}^\circ+45{}^\circ \)
\( \displaystyle 240{}^\circ =180{}^\circ +60{}^\circ \)
\( \displaystyle 240{}^\circ =270{}^\circ -30{}^\circ \)…
В принципе не важно, в какой из двух альтернативных форм для каждой четверти ты представишь угол. На конечном результате это не скажется.
Теперь смотрим, что у нас получилось: если ты выбрал запись через \( \displaystyle 180\) или \( \displaystyle 360\) градусов плюс минус что-либо, то знак функции меняться не будет: ты просто убираешь \( \displaystyle 180\) или \( \displaystyle 360\) и записываешь синус, косинус или тангенс оставшегося угла.
Если же ты выбрал запись через \( \displaystyle 90\) или \( \displaystyle 270\) градусов, то синус меняем на косинус, косинус на синус, тангенс на котангенс, котангенс – на тангенс.
Ставим перед получившимся выражением знак, который мы запомнили.
Давай продемонстрируем все вышесказанное на примерах:
- Вычислить \( \displaystyle sin\ 2130{}^\circ \)
- Вычислить \( \displaystyle \sqrt{2}cos\frac{21\pi }{4}\)
- Найдите значение выражения: \( \displaystyle 12\sin 150{}^\circ \cos 120{}^\circ \)
Начнем по порядку:
Теперь потренируйся самостоятельно на следующих примерах:
- Вычислить \( \displaystyle sin\ 2130{}^\circ \)
- Вычислить \( \displaystyle \sqrt{2}cos\frac{21\pi }{4}\)
- Найдите значение выражения: \( \displaystyle 12\sin 150{}^\circ \cos 120{}^\circ \)
А вот и решения:
Ось тангенсов и ось котангенсов
Последнее, на чем бы мне хотелось здесь остановиться – это на двух дополнительных осях. Как мы уже обсуждали, у нас есть две оси:
- Ось \( \displaystyle X\) – ось косинусов
- Ось \( \displaystyle Y\) – ось синусов
На самом деле, координатные оси у нас закончились, не так ли? Но как же быть с тангенсами и котангенсами?
Неужели, для них нет никакой графической интерпретации?
На самом деле, она есть, ее ты можешь увидеть на вот этой картинке:
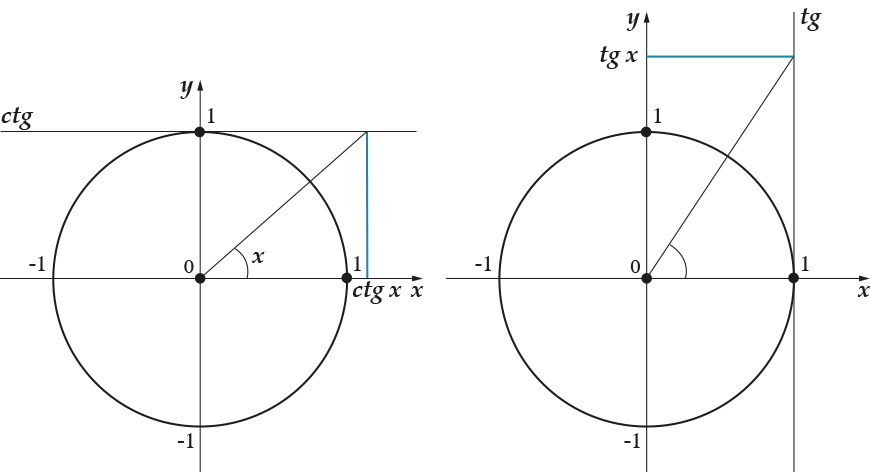
В частности, по этим картинкам можно сказать вот что:
- Тангенс и котангенс имеют одинаковые знаки по четвертям
- Они положительны в 1 и 3 четверти
- Они отрицательны во 2 и 4 четверти
- Тангенс не определен в углах \( \displaystyle \frac{\pi }{2}+\pi k,~k\in Z\)
- Котангенс не определен в углах \( \displaystyle \pi k,~k\in Z\)
Для чего еще нужны эти картинки?
Читай дальше. Я расскажу, как с помощью тригонометрического круга можно упрощать решения тригонометрических уравнений!
Два случая, когда тригонометрическая окружность может пригодиться для решения уравнений
- В ответе у нас не получается «красивый» угол, но тем не менее надо производить отбор корней
- В ответе получается уж слишком много серий корней
Никаких специфических знаний тебе не требуется, кроме знания темы: «Тригонометрические уравнения»
Тему «тригонометрические уравнения» я старался писать, не прибегая к окружности. Многие бы меня за такой подход не похвалили.
Но мне милее формулы, уж что тут поделать. Однако в некоторых случаях формул оказывается мало. Например здесь:
Решите уравнение: \( \displaystyle 8co{{s}^{4}}x-10co{{s}^{2}}x+3=0\)
Решение:
Ну что же. Решить само уравнение несложно.
Замена \( \displaystyle t=co{{s}^{2}}x\).
\( \displaystyle 8{{t}^{4}}-10{{t}^{2}}+3=0\)Корни:
\( \displaystyle {{t}_{1}}=\frac{1}{2},{{t}_{2}}=\frac{3}{4}\)Обратная замена:
\( \displaystyle co{{s}^{2}}x=\frac{1}{2}\), откуда
\( \displaystyle cosx=\frac{\sqrt{2}}{2}~\) или \( \displaystyle cosx=-\frac{\sqrt{2}}{2}\)
Или же:
\( \displaystyle co{{s}^{2}}x=\frac{3}{4}\)Откуда
\( \displaystyle cosx=\frac{\sqrt{3}}{2}\) или \( \displaystyle cosx=-\frac{\sqrt{3}}{2}\)
Отсюда наше исходное уравнение равносильно аж четырем простейшим уравнениям!
Неужели нам нужно будет записывать 4 серии корней?!
Второй пример – уравнения, которые имеют «некрасивые корни».
Например:
- Решите уравнение \( \displaystyle 2sin2x=4cosx-sinx+1\). Найдите его корни, принадлежащие промежутку \( \displaystyle \left[ \frac{\pi }{2},\frac{3\pi }{2} \right]\).
Первая часть не представляет из себя ничего сложного.
Поскольку ты уже знаком с темой «Тригонометрические уравнения», то я позволю себе быть кратким в моих выкладках.
\( \displaystyle 2\cdot 2sin x\cdot cos x=4cos x-sin x+1\) \( \displaystyle 4sin x\cdot cos x-4cos x+sin x-1=0\) \( \displaystyle 4cos x\left( sin x-1 \right)+\left( sin x-1 \right)=0\) \( \displaystyle \left( 4cos x+1 \right)\left( sin x-1 \right)=0\)тогда \( \displaystyle 4cos x+1=0\) или \( \displaystyle \left( sin x-1 \right)=0\)
\( \displaystyle cosx=-\frac{1}{4}\) или \( \displaystyle sinx=1\)
\( \displaystyle x=\pm \text{arccos}\left( -\frac{1}{4} \right)+2\pi n\) или \( \displaystyle x=\frac{\pi }{2}+2\pi n\)
Так мы нашли корни нашего уравнения. Ничего сложного.
Сложнее решить вторую часть задания, не зная, чему в точности равен арккосинус от минус одной четверти (это не табличное значение).
Однако мы можем изобразить найденные серии корней на единичной окружности:
А что насчет тангенсов и котангенсов?
На самом деле, для них тоже есть свои оси, правда они имеют немного специфический вид:

В остальном же способ обращения с ними будет такой же, как с синусом и косинусом.
Напоследок рекомендую тебе самостоятельно решить вот этот пример, прибегая к помощи единичной окружности
- Дано уравнение \( \displaystyle 2co{{s}^{2}}x+2sin2x=3\). Решите данное уравнение. Укажите корни данного уравнения, принадлежащие промежутку \( \displaystyle \left[ -\frac{3\pi }{2},-\frac{\pi }{2} \right]\).
Решение:
\( \displaystyle 2co{{s}^{2}}x+2sin2x=3.\) \( \displaystyle 2co{{s}^{2}}x+4sinxcosx-3\left( si{{n}^{2}}x+co{{s}^{2}}x \right)=0\) \( \displaystyle co{{s}^{2}}x-4sinxcosx+3si{{n}^{2}}x=0\) \( \displaystyle 1-4tgx+3t{{g}^{2}}x=0\) \( \displaystyle t=tgx\) \( \displaystyle 1-4t+3{{t}^{2}}=0\) \( \displaystyle {{t}_{1}}=1,{{t}_{2}}=\frac{1}{3}\)\( \displaystyle tgx=1\), \( \displaystyle x=\frac{\pi }{4}+\pi n\)
\( \displaystyle tgx=\frac{1}{3}\), \( \displaystyle x=arctg\frac{1}{3}+\pi n\)
Рисуем единичную окружность и отмечаем на ней наши решения:
Подведение итогов
- Ты научился делать универсальную шпору по тригонометрии.
- Ты научился решать задачи намного легче и быстрее и, самое главное, без ошибок.
- Ты понял, что тебе не надо зубрить никакие таблицы и вообще мало что нужно зубрить!
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
На этих видео из нашего курса подготовки к ЕГЭ по математике вы можете потренироваться, решая задачи вместе с нашим репетитором Алексеем Шевчуком.
Это разбор задач в режиме реального времени. Тех задач, о которых мы говорили все это время. Вы точно научитесь решать любые задачи на эти темы, если прослушаете.
Хотите получить максимум от этих вебинаров? Берите ручку и бумагу и решайте вместе с Алексеем Шевчуком.
ЕГЭ 9. Тригонометрическая окружность, табличные значения
На этом уроке мы узнаем, что такое тригонометрическая окружность и насколько она важна для тригонометрии.
Мы увидим, что она — основной инструмент в тригонометрии: с её помощью можно вывести любую формулу и найти любые значения.
Мы поймем, как «работает» окружность — а значит, поймём тригонометрию в целом.
ЕГЭ 13б. Тригонометрическая окружность ( 15 минут)
Тригонометрическая окружность — это очень простой и эффективный инструмент для решения любой тригонометрической задачи.
Из этого видео вы узнаете как пользоваться тригонометрической окружностью для решения пункта «б» из задачи №13 профильного ЕГЭ.
ЕГЭ 13б. Отбор корней тригонометрического уравнения. Вебинар (1 час 35 минут)
В этом видео мы усовершенствуем навыки отбора корней тригонометрического уравнения и работы с тригонометрической окружностью.
Ведь окружность — основной инструмент в тригонометрии, с её помощью можно вывести любую формулу и найти любые значения.
Научимся решать пункт б) задачи №13 двумя способами:
- Научимся изображать на окружности формулы вида 0,5π+πn и искать на заданном отрезке значения, соответствующие этим формулам.
- С помощью двойного неравенства.
Подготовка к ЕГЭ на 90+ в мини-группах
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Здравствуйте! Отличный материал, только в некоторых уроках, как в этом, нет решения. Открывали в разных браузерах
Материал классный! Все-все понятно, только не открылись решения для прочтения, хотя зарегистрировалась. Очень хочу почитать другие статьи по математики
Татьяна, попробуйте в другом браузере. Иногда в некоторых браузерах, настройки безопасности не открывают закрытые части. В Сафари, в частности.
Некоторые комментарии прошлых лет к этой статье:
Александр Андреев
20 декабря 2017
Большое спасибо, лучшее объяснение из всех, что читал. Благодаря вам наконец-то понял, как это работает)
Адиль
19 января 2020
Просто огромное спасибо человеку кто это написал А на сколько крутая подача Когда особенно речь о самолётах зашла сразу вдохновением повеяло Счастья и удачи
Иван
26 февраля 2020
Большое спасибо, после прочтения всё сразу стало понятно 🙂