Вписанная окружность
Ну что, юнга, уверен, что знаешь все про окружности?
Пров вписанную точно знаешь. А про вневписанную слышал?
Ничего страшного, сейчас ты во всём разберешься!
Поехали!
Вписанная окружность — коротко о главном
Вписанная в треугольник окружность — окружность, которая касается всех (трёх) сторон треугольника.
В любой треугольник можно вписать окружность, причём единственным образом.
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
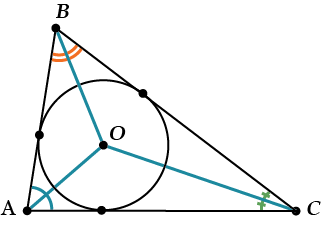
Радиусы вписанной окружности, проведенные в точки касания, перпендикулярны сторонам треугольника: \( \displaystyle OL\bot AB\), \( \displaystyle OM\bot BC\), \( \displaystyle OK\bot AC\).
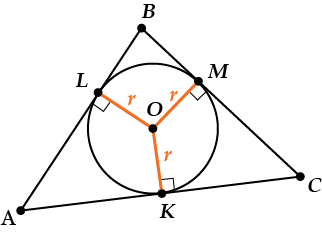
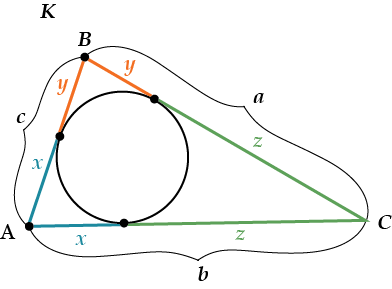
Отрезки от вершин треугольника до точек касания выражаются по формулам:
\( \displaystyle x=\frac{b+c-a}{2}\)\( \displaystyle y=\frac{a+c-b}{2}\)\( \displaystyle z=\frac{a+b-c}{2}\).
Площадь треугольника через радиус вписанной окружности:
\( \displaystyle S=p\cdot r\), где \( \displaystyle p=\frac{a+b+c}{2}\) — полупериметр треугольника, а \( \displaystyle r\) — радиус вписанной окружности.
Вневписанная окружность – окружность, которая касается одной стороны треугольника и продолжений двух других сторон.
Центр вневписанной окружности лежит на пересечении биссектрисы внутреннего угла треугольника (\( \displaystyle \angle A\)) и биссектрис двух внешних углов (\( \displaystyle \angle B\) и \( \displaystyle \angle C\)).
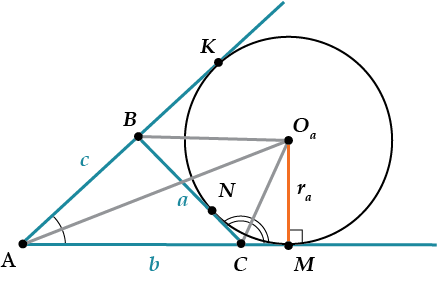
Площадь треугольника через радиус вневписанной окружности:
\( \displaystyle {{S}_{\Delta ABC}}=(p-a)\cdot r\), где \( \displaystyle p=\frac{a+b+c}{2}=AK=AM\) — полупериметр треугольника, а \( \displaystyle r\) — радиус вневписанной окружности.
Вписанная окружность — подробнее
Здесь мы будем говорить об окружностях, связанных с треугольником. Оставим пока в стороне страшное слово «вневписанная» и поговорим об окружности, вписанной в треугольник.
Итак, что же это такое?
Окружность называется вписанной в треугольник, если она касается всех(трёх) его сторон.

Для всякого ли треугольника можно подобрать такую окружность? И как найти ее центр?
На эти вопросы отвечает следующая теорема:
Во всякий треугольник можно вписать окружность, причём единственным образом.
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.

И повторим ещё раз то, что очень нужно запомнить:
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
Если тебя заинтересовал вопрос о том, почему это все три биссектрисы обязаны пересечься, и какое отношение имеют биссектрисы к тому, что окружность касается сторон треугольника, то добро пожаловать к теме «Биссектриса».
Но для начала хватит просто запомнить то, что центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
Теперь немножко о радиусе.
Радиус вписанной окружности
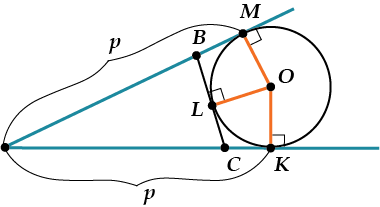
Посмотри, пусть у нас в \( \displaystyle \Delta ABC\) вписана окружность с центром \( \displaystyle O\).
Тогда отрезки \( \displaystyle OK\), \( \displaystyle OL\), и \( \displaystyle OM\) – радиусы этой окружности.
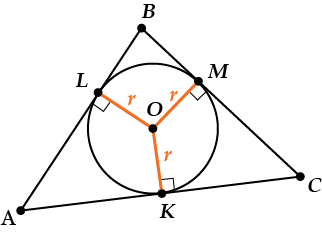
Поэтому они, конечно же, равны, но ещё – они все перпендикулярны сторонам. Это происходит оттого, что радиус, проведенный в точку касания, перпендикулярен касательной.
Итак, запомни и используй:
Радиусы вписанной окружности, проведенные в точки касания, перпендикулярны сторонам треугольника.
Что же ещё?
Вписанная окружность и отрезки сторон треугольника
Давай представим, что мы откуда-то узнали все три стороны треугольника.

Можно ли найти как-то отрезочки \( \displaystyle AK\), \( \displaystyle KC\), \( \displaystyle BL\) и.д. —отрезки, на которые точки касания разбивают стороны треугольника?
Представь себе, можно, и даже очень легко. Для этого нужно знать только то, что отрезки касательных, проведённых из одной точки, равны (если ещё не успел это узнать – загляни в тему «Касательные, касающиеся окружности»).
Итак, начнём поиск!
Посмотри внимательно: из точки \( \displaystyle A\) проведено две касательных, значит их отрезки \( \displaystyle AK\) и \( \displaystyle AM\) равны.
Мы обозначим их «\( \displaystyle x\)».
Далее, точно так же:
\( \displaystyle BM=BL=y\) (обозначили).
\( \displaystyle CK=CL=z\) (обозначили).
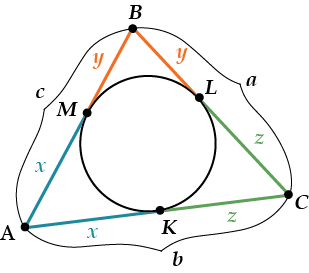
Теперь вспомним-ка, что мы знаем длины всех трёх сторон треугольника. Обозначим эти длины «\( \displaystyle a\)», «\( \displaystyle b\)», «\( \displaystyle c\)» — смотри на рисунок. Что же теперь получилось?
А вот, например, отрезок «\( \displaystyle a\)» состоит из двух отрезков «\( \displaystyle y\)» и «\( \displaystyle z\)», да и отрезки «\( \displaystyle b\)» и «\( \displaystyle c\)» тоже из чего-то состоят. Запишем это всё сразу:
\( \displaystyle \left\{ \begin{array}{l}y+z=a\\x+z=b\\x+y=c\end{array} \right.\)
Ух ты! Выход в алгебру! Три уравнения и три неизвестных! Сейчас решим!
Сложим первые два уравнения и вычтем третье:
\( \displaystyle \left\{ \begin{array}{l}y+z=a\\x+z=b\\x+y=c\end{array} \right.\Rightarrow x+y+2z-\left( x+y \right)=a+b-c\), то есть:
\( \displaystyle z=\frac{a+b-c}{2}\)
А теперь сложим первое и третье уравнение и вычтем второе:
\( \displaystyle \left\{ \begin{array}{l}y+z=a\\x+z=b\\x+y=c\end{array} \right.\Rightarrow y+z+x+y-\left( x+z \right)=a+c-b\), то есть:
\( \displaystyle y=\frac{a+c-b}{2}\)
И последний шаг: сложим второе и третье, а потом вычтем первое.
\( \displaystyle \left\{ \begin{array}{l}y+z=a\\x+z=b\\x+y=c\end{array} \right.\Rightarrow x=\frac{b+c-a}{2}\) \( \displaystyle x=\frac{b+c-a}{2}\)Ну вот, всё нашли:
\( \displaystyle x=\frac{b+c-a}{2};y=\frac{a+c-b}{2};~z=\frac{a+b-c}{2}\)
Очень много плюсов и минусов – аж в глазах рябит. Как же это запомнить? А оказывается, очень просто. Смотри-ка на картинку и формулу сразу.

Секрет вот в чём: те стороны, на которых есть «\( \displaystyle x\)» («\( \displaystyle b\)» и «\( \displaystyle c\)») будут с плюсом, а та сторона, где нет «\( \displaystyle x\)» (это «\( \displaystyle a\)»), будет с минусом.
Ну, а пополам поделить всё хозяйство. С другими буквами точно так же
\( \displaystyle y=\frac{a+c-b}{2}\)
На «\( \displaystyle a\)» и «\( \displaystyle c\)» есть «\( \displaystyle y\)» — они с плюсом, на «\( \displaystyle b\)» нет «\( \displaystyle y\)» — она с минусом
\( \displaystyle z=\frac{a+b-c}{2}\)
На «\( \displaystyle a\)» и «\( \displaystyle b\)» есть «\( \displaystyle z\)» — они с плюсом, на «\( \displaystyle c\)» нет «\( \displaystyle z\)» — она с минусом.
Вписанная окружность и площадь
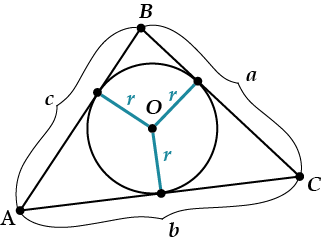
Здесь скажем совсем коротко:
Есть такая формула:
\( \huge\displaystyle S=p\cdot r\),
где \( \displaystyle p\) — это полупериметр треугольника, то есть \( \displaystyle p=\frac{a+b+c}{2}\), а \( \displaystyle r\) — радиус вписанной окружности.
Вневписанная окружность
Ну вот, пора приступать к самому непонятному. Что же это за зверь такой: «вневписанная окружность»? Сначала посмотри на картинку:

Видишь, окружность тоже чего-то касается, но «сидит» как-то снаружи, вне треугольника? Вот поэтому и называется вневписанной.
Окружность называется вневписанной для треугольника, если она касается ОДНОЙ стороны треугольника и продолжений двух других сторон.
А как ты думаешь, сколько у одного треугольника может быть вневписанных окружностей? Вот, представь себе, аж три!
Посмотри, вот так:

Захватывает дух? Насладись впечатлением.
А еще подумай над тем…
- откуда взялся \( \displaystyle \Delta {{O}_{1}}{{O}_{2}}{{O}_{3}}\);
- что это за точка \( \displaystyle O\);
- что это вообще за тьма линий на рисунке.
А сейчас вернёмся к одной какой-нибудь вневписанной окружности и узнаем всего один, но очень важный факт:
До дальней точки касания вневписанной окружности ровно полупериметр
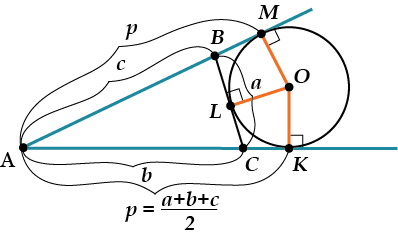
\( \displaystyle AK=AM=\frac{a+b+c}{2}\),
или что то же самое: \( \displaystyle AK=AM=p\), где \( \displaystyle p\) — полупериметр.
Доказывать не будем, но ещё раз посмотри и запомни:
До «дальней» точки касания вневписанной окружности – ровно полупериметр треугольника.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Андрей
11 июля 2018
Прекрасное обьяснение, спасибо большое!
Александр (админ)
12 июля 2018
И тебе спасибо, Андрей. За теплые слова.
Юлия
09 сентября 2018
все просто и понятно, спасибо большое!
Александр (админ)
09 сентября 2018
И тебе спасибо, Юлия! Очень приятно слышать!
Миша
28 сентября 2018
не подскажите, почему отрезок о3б перпендикулярен отрезку о1о2?
Александр
21 августа 2019
Это биссектрисы смежных углов.
Денис
24 февраля 2019
Божественные рисунки!) Мне в школе для урока по геометрии надо подготовить несколько рисунков. Подскажите, пожалуйста, какой программой вы пользуетесь для построения рисунков?
Александр (админ)
07 марта 2019
Денис, прошу прощения, пост твой пропустил. Только сейчас отвечаю. Но врядли чем-то помогу. Рисунки делались так: сначала их от руки делала Елена Евгеньевна (наш математик), а потом профессиональный дизайнер Настя их перерисовывала. По-моему в фотошопе.