Секущая и хорда окружности
Зачем что-то знать о секущих и хордах в окружности?
Как обычно, знание свойств и закономерностей сильно облегчает жизнь.
Зная свойства секущих и хорд в окружности и закономерности (формулы), мы сможем решить многие задачи на ЕГЭ!
Поехали!
Секущая и хорда окружности — коротко о главном
Секущая окружности
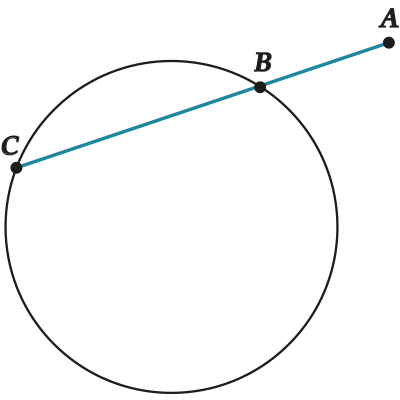
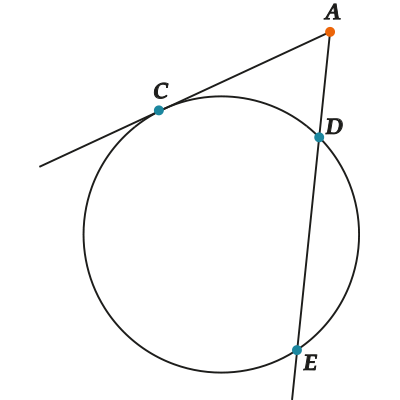
Здесь \( \displaystyle AC\) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках.
Хорда окружности
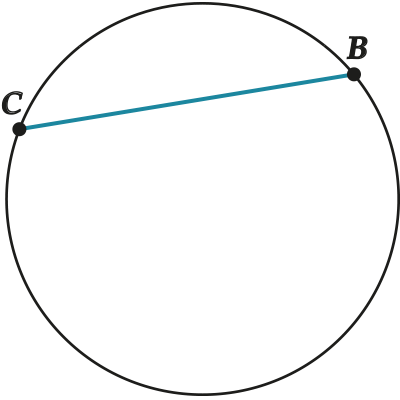
Здесь \( \displaystyle BC\) – хорда окружности – отрезок, соединяющий две точки на окружности.
Длина хорды
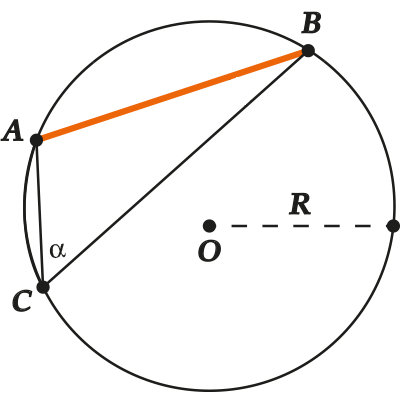
Пусть \( \displaystyle AB\) – хорда, \( \displaystyle R\) – радиус, \( \displaystyle \angle AСB\) – любой вписанный угол, опирающийся на хорду \( \displaystyle AB\). Тогда:
\( \displaystyle AB=2R\sin \alpha\).
Произведение длин отрезков хорд и секущих
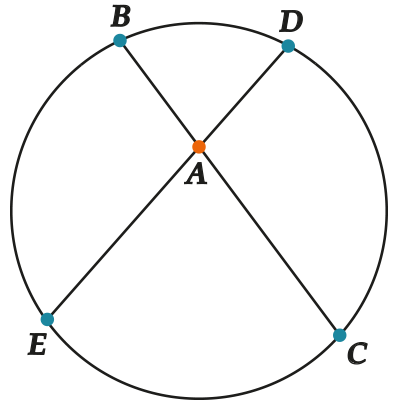
Для любых двух хорд, проходящих через некоторую точку \( \displaystyle A\), выполняется:
\( \displaystyle AB\cdot AC=AD\cdot AE\).
Теорема о секущей и касательной
Для любых секущей и касательной, проходящих через точку \( A\), верно:
\( \displaystyle A{{C}^{2}}=AD\cdot AE\).
А теперь подробнее…
Определения секущей и хорды окружности
Давай прежде всего вспомним, что такое секущая и хорда. Смотри на картинки.
Здесь \( \displaystyle AC\) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках.

Здесь \( \displaystyle BC\) – хорда окружности – отрезок, соединяющий две точки на окружности.

Кстати, заметил ли ты, что на первом рисунке хорда \( \displaystyle BC\) является кусочком секущей \( \displaystyle AC\)?
Вот так всегда и бывает: если есть секущая, то один её кусок – хорда, а второй называется внешняя часть, ну, как у нас \( \displaystyle AB\) – она же снаружи, верно?
Что же мы должны знать о секущей и хорде окружности?
Всего-то 2-3-4 утверждения. Давай начнём с того, что ты, возможно, уже читал в разделе «Теорема синусов» и «Теорема косинусов» — с длины хорды в окружности.
Длина хорды окружности
Пусть \( \displaystyle AB\) – хорда, \( \displaystyle R\) – радиус, \( \displaystyle \angle ACB\) – любой вписанный угол, опирающийся на хорду \( \displaystyle AB\).
Тогда \( \Large\frac{AB}{\sin \alpha }=2R\)

Узнал теорему синусов?
Значит, длину хорды окружности можно найти по формуле:
Произведение длин отрезков хорд и секущих
Сейчас мы сформулируем очень важное, пожалуй, даже основное свойство хорд и секущих окружности.
Словами это свойство формулировать неудобно – получается длинно и некрасиво, поэтому ограничимся буквами.
Произведение длин отрезков хорд окружности
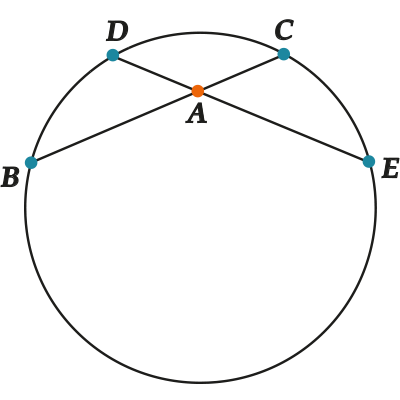
Для любых двух хорд окружности, проходящих через некоторую точку \( \displaystyle A\), выполняется: \( \displaystyle AB\cdot AC=AD\cdot AE\)

Произведение длин отрезков секущих окружности
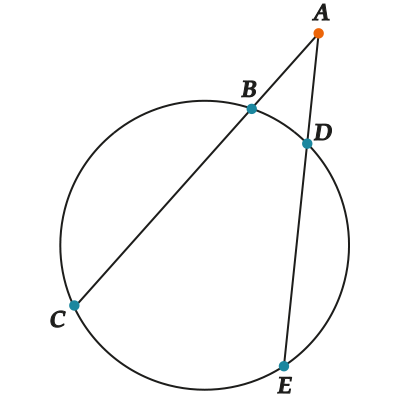
Для любых двух секущих, проходящих через некоторую точку \( \displaystyle A\), выполняется: \( \displaystyle AB\cdot AC=AD\cdot AE\)
Вопрос первый: Почему мы сформулировали утверждения друг под другом столбиком?
Ответ: Утверждения очень похожи – если закрыть картинки и слова, то получится просто одно и то же – удивительно, не правда ли? Ну, и это сходство гораздо лучше видно, когда утверждения стоят рядом.
Вопрос второй: Как не перепутать, что на что умножать?
Произведение длин отрезков хорд окружности — доказательство
Повторим формулировку.
Для любых двух хорд, проходящих через некоторую точку \( \displaystyle A\), выполняется: \( AB\cdot AC=AD\cdot AE\)
А теперь докажем.
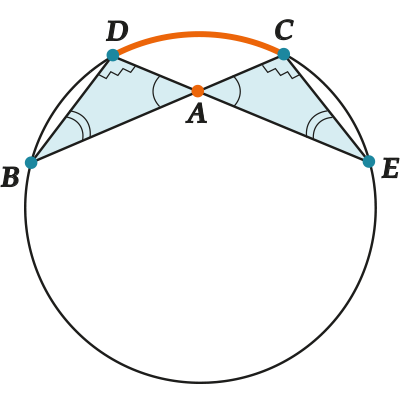
Рассмотрим \( \triangle ABD\) и \( \triangle AEC\). У них углы \( \displaystyle A\) равны как вертикальные и \( \angle DBC=\angle DEC\), потому что они опираются на одну дугу \( \displaystyle DC\).
Значит, \( \displaystyle \triangle ABD\sim \triangle AEC\) по двум углам (вспоминаем признаки подобия треугольников).
Запишем, что же нам даёт это подобие (и откроем маленький секрет!).
Произведение длин отрезков секущих окружности — доказательство
Еще раз формулировку…
Для любых двух секущих, проходящих через некоторую точку \( \displaystyle A\), выполняется: \( AB\cdot AC=AD\cdot AE\)
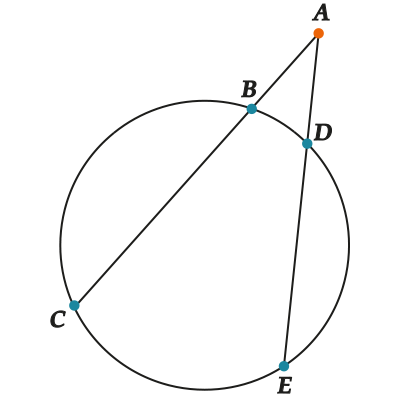
Снова рассмотрим \( \displaystyle \triangle ABD\) и \( \displaystyle \triangle AEC\).
- У них есть общий \( \angle A\);
- Четырехугольник \( BCED\) — вписанный (срочно повторяем или читаем тему «Окружность. Вписанный угол»).
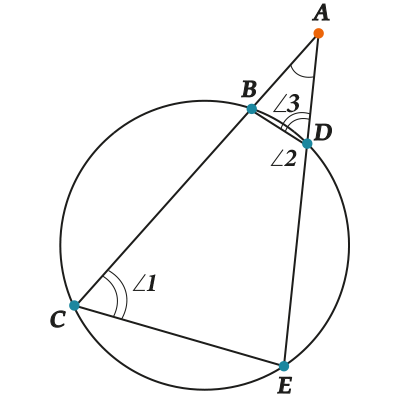
Значит, \( \angle 1+\angle 2=180{}^\circ \) (сумма противоположных углов вписанного четырехугольника равна \( 180{}^\circ \)). Но \( \angle 2+\angle 3=180{}^\circ \) — как смежные углы (смотри на картинку).
Что же получилось?
\( \left\{ \begin{array}{l}\angle 1+\angle 2=180{}^\circ \\\angle 2+\angle 3=180{}^\circ \end{array} \right.\Rightarrow \angle 1=\angle 3\)
То есть \( \underbrace{\angle ACE}_{в\ \triangle AEC}=\underbrace{\angle ADB}_{в\ \triangle ABD\ }\).
Из всего этого следует, что \( \triangle AEC\sim \triangle ABD\) по двум углам (\( \angle A\) – общий и \( \angle ACE=\angle ADB\)).
Снова запишем отношение соответствующих сторон:
Теорема о секущей и касательной (секретное оружие)
А сейчас «секретное» оружие — теорема о секущей и касательной. Почему секретное?
Потому что множество задач ОГЭ и ЕГЭ можно решить с помощью этой теоремы. А акцент на ней в учебнике не делается. То есть ее как бы нет…
В предыдущем пункте мы выяснили, что \( AB\cdot AC=AD\cdot AE\)

Но возникает вопрос: а что будет, если секущая \( AC\) и «превратится» в касательную?
Видишь: осталось всего три зелёных точки? Оказывается, ничего страшного, всё почти так же. Формулируем:
Для любых секущей и касательной, проходящих через точку \( A\), верно: \( \Large A{{C}^{2}}=AD\cdot AE\).
Тут точки \( B\) и \( C\) как бы слились в одну – и на рисунке, и в формуле. Заметил?

Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



А если секущая пройдет через диаметр? То ответы не совпадут, если задачу решить по теореме Пифагора и с помощью данной формулы . найти АС, если АD=10, DE=75// В одном случае 40, а в другом корень из 850. Почему?
Надежда, очень классный подход — проверять решение на частных случаях и пробовать решить задачу разными способами! Теперь давай проверим решение через треугольник: как получился ответ 40? Что было гипотенузой в этом треугольнике, а что известным катетом?
Замечательное обьяснение
Спасибо, Маша!
Шикарная статья! Формат изложения ВЕЛИКОЛЕПНЫЙ! Спасибо!
Спасибо, Александр! Заходите… очень приятно слышать.
Некоторые комментарии прошлых лет к этой статье:
Богдан
15 ноября 2018
Спасибо огромное!
Любовь
25 января 2019
Да, замечательно все и очень понятно. Спасибо за ваш труд
Енот — полоскун
02 апреля 2019
Потрясающе, спасибо огромное!
Уля
03 апреля 2019
ВЫ МНЕ ОЧЕНЬ ПОМОГЛИ , СПАСИБО ОГРОМНОЕ ВАМ !
Ророша
17 мая 2019
Наконец-то теперь я поняла, спасибо большое
Лилит
10 июня 2019
Супер! Спасибо. Все очень просто и понятно.