Свойства корней
А сейчас мы рассмотрим свойства корней.
Квадратный корень, кубический корень и корень в N-ой степени.
Порешаем задачки, чтобы к концу этого занятия все, что касается корней (в любой степени) было тебе абсолютно понятно!
И, самое главное, чтобы ты смог решить любую задачу c корнями на экзамене!Поехали!
Свойства корней — коротко о главном
Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\)
\( \left( \sqrt{a}=x,\ {{x}^{2}}=a;\ \ x,a\ge 0 \right)\)
Свойства корней:
Для любого натурального \( n\), целого \( k\) и любых неотрицательных чисел \( a\) и \( b\) выполнены равенства:
| \( \sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b};\) |
| \( \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\text{ }\left( b\ne 0 \right);\) |
| \( \sqrt[n]{\sqrt[k]{a}}=\sqrt[nk]{a}\text{ }\left( k>0 \right);\) |
| \( \sqrt[nk]{{{a}^{k}}}=\sqrt[n]{a}\text{ }\left( k>0 \right);\) |
| при нечетных \( n\): \( \sqrt[n]{{{a}^{k}}}={{\left( \sqrt[n]{a} \right)}^{k}}\text{ }\left( \text{если }k\le 0,\text{ }то\text{ }a\ne 0 \right)\) |
| при четных \( k\) и \( n\): \( \sqrt[n]{{{a}^{k}}}={{\left( \sqrt[n]{\left| a \right|} \right)}^{k}}\text{ }\left( \text{если }k\le 0,\text{ то }a\ne 0 \right)\) |
Арифметический квадратный корень
Когда ты разберешься в этой теме, тебе станет намного легче решать иррациональные уравнения и неравенства.
А пока что давай попробуем разобраться, что это за понятие «корень» и с чем его едят 🙂
Для этого рассмотрим примеры, с которыми ты уже сталкивался на уроках (ну, или тебе с этим только предстоит столкнуться).
К примеру, перед нами уравнение \( {{x}^{2}}=4\). Какое решение у данного уравнения? Какие числа можно возвести в квадрат и получить при этом \( 4\)?
Вспомнив таблицу умножения, ты легко дашь ответ: \( 2\) и \( -2\) ( ведь при перемножении двух отрицательных чисел получается число положительное)!
Для упрощения, математики ввели специальное понятие квадратного корня и присвоили ему специальный символ \( \sqrt{\ \ }\).
Дадим определение арифметическому квадратному корню.
Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\)
\( \left( \sqrt{a}=x,\ {{x}^{2}}=a;\ \ x,a\ge 0 \right)\)
А почему же число \( a\) должно быть обязательно неотрицательным?
Например, чему равен \( \sqrt{-9}\). Так-так, попробуем подобрать. Может, три?
Проверим: \( {{3}^{2}}=9\), а не \( -9\). Может, \( \left( -3 \right)\)? Опять же, проверяем: \( {{\left( -3 \right)}^{2}}=9\). Ну что же, не подбирается? Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число!
Это надо запомнить: число или выражение под знаком корня должно быть неотрицательным!
Однако самые внимательные уже наверняка заметили, что в определении сказано, что решение квадратного корня из «числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\)».
Кто-то из вас скажет, что в самом начале мы разбирали пример \( {{x}^{2}}=4\), подбирали числа, которые можно возвести в квадрат и получить при этом \( 4\), ответ было \( 2\) и \( -2\), а тут говорится про какое-то «неотрицательное число»!
Такое замечание вполне уместно. Здесь необходимо просто разграничить понятия квадратных уравнений и арифметического квадратного корня из числа.
Квадратное уравнение или квадратный корень?
К примеру, \( {{x}^{2}}=4\) не равносильно выражению \( x=\sqrt{4}\).
Из \( {{x}^{2}}=4\) следует, что \( \left| x \right|=\sqrt{4}\), то есть \( x=\pm \sqrt{4}=\pm 2\) или \( {{x}_{1}}=2;\ {{x}_{2}}=-2\).
(Читай тему «Модуль числа»)
А из \( x=\sqrt{4}\) следует, что \( x=2\).
Конечно, это очень путает, но это необходимо запомнить, что знаки являются результатом решения уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.
В наше квадратное уравнение подходит как \( 2\), так и \( -2\).
Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.
А теперь попробуй решить такое уравнение \( {{x}^{2}}=3\).
Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?
Начнем с самого начала – с нуля: \( {{0}^{2}}=0\) – не подходит.
Двигаемся дальше \( \text{x}=1;\ {{1}^{2}}=1\) – меньше трех, тоже отметаем.
А что если \( x=2\); \( {{2}^{2}}=4\) – тоже не подходит, т.к. это больше трех.
С отрицательными числами получится такая же история.
И что же теперь делать? Неужели перебор нам ничего не дал?
Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между \( 1\) и \( 2\), а также между \( -2\) и \( -1\).
Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными. И что дальше?
Давай построим график функции \( y={{x}^{2}}\) и отметим на нем решения. (Прочти по ссылке как использовать график функции для решения уравнений)
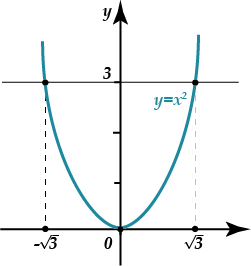
Давай попробуем обмануть систему и получить ответ с помощью калькулятора! Извлечем корень из \( 3\), делов-то! Ой-ой-ой, выходит, что \( \sqrt{3}=1,732050807568…\).
Такое число никогда не кончается.
Как же такое запомнить, ведь на экзамене калькулятора не будет!? Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. \( \sqrt{3}\) и \( -\sqrt{3}\) уже сами по себе ответы.
Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.
Рассмотрим еще один пример для закрепления.
Разберем такую задачку: тебе необходимо пересечь по диагонали квадратное поле со стороной \( \displaystyle 1\) км, сколько км тебе предстоит пройти?
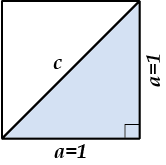
Самое очевидное здесь рассмотреть отдельно треугольник и воспользоваться теоремой Пифагора: \( {{c}^{2}}={{a}^{2}}+{{a}^{2}}\). Таким образом, \( {{c}^{2}}=1+1=2\).
Так чему же здесь равно искомое расстояние?
Очевидно, что расстояние не может быть отрицательным, получаем, что \( c=\sqrt{2}\). Корень из двух приблизительно равен \( 1,41\), но, как мы заметили раньше, \( \sqrt{2}\) -уже является полноценным ответом.
Чтобы решение примеров с корнями не вызывало проблем, необходимо их видеть и узнавать. Для этого необходимо знать, по меньшей мере, квадраты чисел от \( 1\) до \( 20\), а также уметь их распознать.
К примеру, необходимо знать, что \( 15\) в квадрате равно \( 225\), а также, наоборот, что \( 225\) – это \( 15\) в квадрате.
Вот тебе полная таблица квадратов чисел. Сверху строка — основание степени, слева в столбик показатель степени, на пересечение искомое значение степени. Запомнить нужно только то, что выделено зеленым.
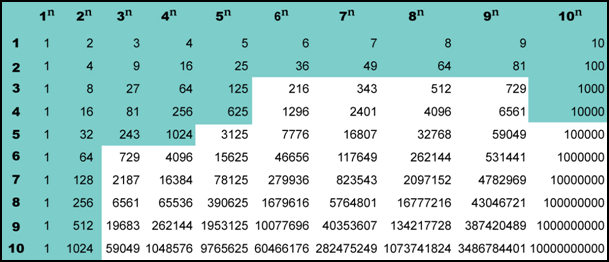
Уловил, что такое квадратный корень? Тогда порешай несколько примеров.
Примеры для самостоятельного решения
- \( \sqrt{0}=?\)
- \( \sqrt{36}=?\)
- \( \sqrt{324}=?\)
- \( \sqrt{256}=?\)
- \( \sqrt{0,81}=?\)
- \( \sqrt{0,01}=?\)
- \( \sqrt{0,0144}=?\)
Ответы:
\( 0;\ 6;\ 18;\ 16;\ 0,9;\ 0,1;\ 0,12\).
Кубический корень
Ну что же, с понятием квадратного корня вроде разобрались, теперь постараемся разобраться, что такое кубический корень и в чем их отличие.
Кубический корень из некоторого числа \( a\) – это число, куб которого равен \( a\). Заметили, тут все гораздо проще?
Здесь нет никаких ограничений на возможные значения как значения под знаком кубического корня, так и извлекаемого числа.
То есть кубический корень можно извлечь из любого числа: \( \sqrt[3]{-27}=-3;\ \sqrt[3]{27}=3\).
Уловили, что такое кубический корень и как его извлекать? Тогда вперед решать примеры.
Решим несколько примеров
- \( \sqrt[3]{-125}=?\)
- \( \sqrt[3]{125}=?\)
- \( \sqrt[3]{64}=?\)
- \( \sqrt[3]{-8}=?\)
- \( \sqrt[3]{-216}=?\)
- \( \sqrt[3]{-64}=?\)
- \( \sqrt[3]{216}=?\)
Ответы:
Корень N-ой степени
Ну что ж, мы разобрались с понятиями квадратного и кубического корня. Теперь обобщим полученные знания понятием корень \( n\)-ой степени.
Корень \( n\) -ой степени из числа \( a\)— это число, \( n\) -ая степень которого равна \( a\), т.е.
\( c=\sqrt[n]{a}\) равносильно \( {{c}^{n}}=a\).
Если \( n\) – чётно, то:
- при отрицательном \( a\), выражение не имеет смысла (корни четной \( n\)-ой степени из отрицательных чисел извлечь нельзя!);
- при неотрицательном \( a\) (\( \left( a\ge 0 \right)\)) выражение имеет один неотрицательный корень.
Если \( n\) – нечётно, то выражение имеет единственный корень при любом \( a\).
Не пугайтесь, тут действуют такие же принципы, что и с квадратными и кубическими корнями. То есть принципы, которые мы применяли при рассмотрении квадратных корней, распространяем на все корни четной \( n\)-ой степени.
А те свойства, которые применяли для кубического корня, распространяются на корни нечетной \( n\)-ой степени.
Ну что, стало понятней? Давайте разбираться на примерах:
\( \sqrt[4]{10000}=?\)
Тут все более ли менее понятно: сначала смотрим – ага, \( 4\) степень – четная, под корнем число положительное, значит наша задача – найти такое число, четвертая степень которого даст нам \( 10000\).
Ну, есть предположения? Может, \( 10\)? Точно, \( {{10}^{4}}=10000\)!
\( \sqrt[5]{-243}=?\)
Так, степень равна \( 5\) – нечетная, под корнем число отрицательное. Наша задача – найти такое число, при возведении которого в \( 5\) степень получается \( \left( -243 \right)\).
Сразу заметить корень довольно затруднительно. Однако можно сразу сузить область поиска, правда?
Во-первых, определенно искомое число отрицательно, а во-вторых, можно заметить, что \( \left( -243 \right)\) – нечетное, а значит и искомое число – нечетное. Попробуй подобрать корень.
Основные свойства корней
Для любого натурального \( n\), целого \( k\) и любых неотрицательных чисел \( a\) и \( b\) выполнены равенства:
| \( \sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b};\) |
| \( \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\text{ }\left( b\ne 0 \right);\) |
| \( \sqrt[n]{\sqrt[k]{a}}=\sqrt[nk]{a}\text{ }\left( k>0 \right);\) |
| \( \sqrt[nk]{{{a}^{k}}}=\sqrt[n]{a}\text{ }\left( k>0 \right);\) |
| при нечетных \( n\): \( \sqrt[n]{{{a}^{k}}}={{\left( \sqrt[n]{a} \right)}^{k}}\text{ }\left( \text{если }k\le 0,\text{ }то\text{ }a\ne 0 \right)\) |
| при четных \( k\) и \( n\): \( \sqrt[n]{{{a}^{k}}}={{\left( \sqrt[n]{\left| a \right|} \right)}^{k}}\text{ }\left( \text{если }k\le 0,\text{ то }a\ne 0 \right)\) |
Понятно? Если нет, то рассмотрев примеры, все должно встать на свои места.
Действия с корнями
Умножение корней
Как умножать корни? На этот вопрос помогает ответить самое простое и базовое свойство:
\( \sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b}\)
Начнем с простенького:
\( \sqrt{5}\cdot \sqrt{2}=\sqrt{10}\)
\( \sqrt{2}\cdot \sqrt{3}=\sqrt{6}\)
Корни из получившихся чисел ровно не извлекаются? Не беда – вот вам такие примеры:
\( \sqrt{2}\cdot \sqrt{8}=\sqrt{16}=4\)
\( \sqrt{12,5}\cdot \sqrt{2}=\sqrt{25}=5\)
А что, если множителей не два, а больше? То же самое! Формула умножения корней работает с любым количеством множителей:
\( \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{10}=\sqrt{100}=10\)
С этим вроде все ясно. Едем дальше. А если перед нами такое выражение:
\( 3\sqrt{5}\)
Что мы можем с ним сделать? Ну конечно, спрятать тройку под корнем, помня при этом, что тройка – корень квадратный из \( 9\)!
\( 3\sqrt{5}=\sqrt{9}\cdot \sqrt{5}=\sqrt{45}\).
Зачем нам это нужно? Да просто, чтобы расширить наши возможности при решении примеров:
\( 3\sqrt{10}-\sqrt{45}\cdot \sqrt{2}=\sqrt{90}-\sqrt{90}=0\).
Как тебе такое свойство корней? Существенно упрощает жизнь? По мне, так точно!
Только надо помнить, что вносить под знак корня четной степени мы можем только положительные числа.
Посмотрим, где это еще может пригодиться. Например, в задаче требуют сравнить два числа:
Что больше: \( 3\sqrt{7}\ или\ 2\sqrt{17}\)?
Сходу и не скажешь. Ну что, воспользуемся разобранным свойством внесения числа под знак корня? Тогда вперед:
До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!
\( \sqrt{98}=\sqrt{49\cdot 2}=\sqrt{49}\cdot \sqrt{2}=7\sqrt{2}\)
Можно было пойти по иному пути и разложить на другие множители:
\( \sqrt{98}=\sqrt{7\cdot 14}\)
Что дальше? А дальше раскладываем на множители до самого конца:
Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:
\( \sqrt{15}\cdot \sqrt{180}\cdot \sqrt{12}\)
Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:
\( \sqrt{15}\cdot \sqrt{180}\cdot \sqrt{12}=\sqrt{5\cdot 3}\cdot \sqrt{36\cdot 5}\cdot \sqrt{2\cdot 6}\)
Разве это конец? Не останавливаемся на полпути!
\( \begin{array}{l}\sqrt{5\cdot 3}\cdot \sqrt{36\cdot 5}\cdot \sqrt{2\cdot 6}=\sqrt{5\cdot 3}\cdot \sqrt{3\cdot 12\cdot 5}\cdot \sqrt{2\cdot 3\cdot 2}=\\=\sqrt{5\cdot 3}\cdot \sqrt{3\cdot 2\cdot 2\cdot 3\cdot 5}\cdot \sqrt{2\cdot 3\cdot 2}\end{array}\)
На простые множители разложили. Что дальше?
А теперь попробуй вот такой пример решить:
\( \sqrt{4225}=?\)
А пример-то – крепкий орешек, так сходу и не разберешься, как к нему подступиться. Но нам он, конечно, по зубам.
Ну что, начнем раскладывать \( 4225\) на множители?
Деление корней
С умножение корней разобрались, теперь приступим к свойству деления.
Напомню, что формула в общем виде выглядит так:
\( \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\text{ }\left( b\ne 0 \right);\)
А значит это, что корень из частного равен частному корней.
Ну что, давай разбираться на примерах:
\( \frac{\sqrt{12}}{\sqrt{3}}=\sqrt{\frac{12}{3}}=\sqrt{4}=2\)
Вот и вся наука. А вот такой пример:
\( \frac{\sqrt{12}}{3}=\frac{\sqrt{12}}{\sqrt{9}}=\sqrt{\frac{12}{9}}=\sqrt{\frac{4}{3}}\)
Все не так гладко, как в первом примере, но, как видишь, ничего сложного нет.
А что, если попадется такое выражение:
\( \sqrt{\frac{144}{225}}=?\)
Надо просто применить формулу в обратном направлении:
\( \sqrt{\frac{144}{225}}=\frac{\sqrt{144}}{\sqrt{225}}=\frac{12}{15}=\frac{4}{5}=0,8\)
А вот такой примерчик:
\( \sqrt{0,16}=\sqrt{\frac{16}{100}}=\frac{4}{10}=0,4\)
А вот если встретить такое выражение:
\( \sqrt{5\frac{19}{25}}=?\)
Все то же самое, только здесь надо вспомнить, как переводить дроби (читай тему «Дроби, рациональные числа»). Вспомнили? Теперь решаем!
А что же будет, если квадратный корень возвести в квадрат?
Все просто, вспомним смысл квадратного корня из числа \( a\) – это число, квадратный корень которого равен \( a\).
Так вот, если мы возводим число, квадратный корень которого равен \( a\), в квадрат, то что получаем? Ну, конечно, \( a\)!
Рассмотрим на примерах:
\( {{\left( \sqrt{12} \right)}^{2}}=12\)
\( {{\left( \sqrt{17} \right)}^{2}}=17\)
Все просто, правда? А если корень будет в другой степени? Ничего страшного! Придерживайся той же логики и помни свойства и возможные действия со степенями (читай тему «Степень и ее свойства»).
Вот, к примеру, такое выражение:
\( {{\left( \sqrt{5} \right)}^{6}}={{\left( {{\left( \sqrt{5} \right)}^{2}} \right)}^{3}}={{5}^{3}}=125\)
В этом примере степень четная, а если она будет нечетная? Опять же, примени свойства степени и разложи все на множители:
\( {{\left( \sqrt{5} \right)}^{7}}={{\left( \sqrt{5} \right)}^{6}}\cdot \sqrt{5}=125\sqrt{5}\)
С этим вроде все ясно, а вот как извлечь корень из числа в степени? Вот, к примеру, такое:
\( \sqrt{{{3}^{2}}}=\sqrt{9}=3\)
Довольно просто, правда? А если степень больше двух? Следуем той же логики, используя свойства степеней:
\( \sqrt{{{3}^{6}}}=\sqrt{{{\left( {{3}^{3}} \right)}^{2}}}={{3}^{3}}=27\)
\( \sqrt{{{3}^{5}}}=\sqrt{{{3}^{4}}\cdot 3}=\sqrt{{{\left( {{3}^{2}} \right)}^{2}}\cdot 3}={{3}^{2}}\cdot \sqrt{3}=9\sqrt{3}\)
Ну как, все понятно? Тогда вот такой пример:
\( \sqrt{{{\left( -3 \right)}^{2}}}=\sqrt{9}=3\)
\( \sqrt[3]{{{\left( -3 \right)}^{3}}}=\sqrt[3]{-27}=-3\)
Это подводные камни, о них всегда стоит помнить. Это фактически и есть отражение на примерах свойства:
при нечетных \( n\): \( \sqrt[n]{{{a}^{k}}}={{\left( \sqrt[n]{a} \right)}^{k}}\text{ }\left( \text{если }k\le 0,\text{ }то\text{ }a\ne 0 \right)\)
при четных \( k\) и \( n\): \( \sqrt[n]{{{a}^{k}}}={{\left( \sqrt[n]{\left| a \right|} \right)}^{k}}\text{ }\left( \text{если }k\le 0,\text{ то }a\ne 0 \right)\)
Понятно? Закрепляй на примерах:
\( \sqrt[4]{{{\left( -3 \right)}^{4}}}=?\)
Ага, видим, корень в четной степени, отрицательное число под корнем тоже в четной степени. Ну и то же получается? А вот что:
\( \sqrt[4]{{{\left( -3 \right)}^{4}}}={{\left( \sqrt[4]{\left| -3 \right|} \right)}^{4}}={{\left( \sqrt[4]{3} \right)}^{4}}=3\)
Вот и все! Теперь вот такие примеры:
\( \sqrt[3]{{{\left( -125 \right)}^{4}}}={{\left( \sqrt[3]{\left( -125 \right)} \right)}^{4}}={{\left( -5 \right)}^{4}}=625\)
\( \sqrt[3]{{{\left( -27 \right)}^{5}}}={{\left( \sqrt[3]{\left( -27 \right)} \right)}^{5}}={{\left( -3 \right)}^{5}}=-243\)
Уловил? Тогда вперед решать примеры.
- \( \sqrt[4]{{{\left( -3 \right)}^{8}}}=?\)
- \( \sqrt[3]{{{\left( -27 \right)}^{4}}}=?\)
- \( \sqrt[3]{{{\left( -125 \right)}^{5}}}=?\)
Ответы:
Посмотрим на два других свойства корней:
\( \sqrt[n]{\sqrt[k]{a}}=\sqrt[nk]{a}\text{ }\left( k>0 \right)\);
\( \sqrt[nk]{{{a}^{k}}}=\sqrt[n]{a}\text{ }\left( k>0 \right)\)
Эти свойства обязательно надо разбирать в примерах. Ну что, займемся этим?
\( \sqrt[3]{\sqrt[4]{3}}=\sqrt[3\cdot 4]{3}=\sqrt[12]{3}\)
\( \sqrt[4]{{{3}^{2}}}=\sqrt[2\cdot 2]{{{3}^{2}}}=\sqrt[2]{3}\)
Понятно? Давай закрепим.
- \( \sqrt[4]{\sqrt[3]{37}}=?\)
- \( \sqrt[5]{\sqrt[7]{6}}=?\)
- \( \sqrt[6]{\sqrt[4]{15}}=?\)
- \( \sqrt[4]{{{5}^{2}}}=?\)
- \( \sqrt[6]{{{7}^{3}}}=?\)
- \( \sqrt[14]{{{5}^{7}}}=?\)
Повторим и подведем итоги
Арифметический квадратный корень
Уравнение \( {{x}^{2}}=4\) имеет два решения: \( x=2\) и \( x=-2\). Это числа, квадрат которых равен \( 4\).
Рассмотрим уравнение \( {{x}^{2}}=3\). Решим его графически. Нарисуем график функции \( y={{x}^{2}}\) и линию на уровне \( y=3\). Точки пересечения этих линий и будут решениями.
Видим, что и у этого уравнения два решения – одно положительное, другое отрицательное:

Но в данном случае решения не являются целыми числами. Более того, они не являются рациональными. Для того, чтобы записать эти иррациональные решения, мы вводим специальный символ квадратного корня \( \sqrt{\ \ }\).
Арифметический квадратный корень \( \sqrt{a}\) — это неотрицательное число, квадрат которого равен\( a,\text{ }a\ge 0\). При \( a<0\) выражение \( \sqrt{a}\) не определено, т.к. нет такого числа, квадрат которого равен отрицательному числу \( a\).
Корень из квадрата: \( \sqrt{{{a}^{2}}}=\left| a \right|\).
Например, \( \sqrt{4}=2\). А из \( {{x}^{2}}=3\) следует, что \( \left| x \right|=\sqrt{3}\Rightarrow x=\sqrt{3}\) или \( x=-\sqrt{3}\).
Еще раз обращаю внимание, это очень важно: Квадратный корень – это всегда неотрицательное число: \( \sqrt{a}\ge 0\)!
Кубический корень из числа \( a\ \left( \sqrt[3]{a} \right)\) — это число, куб которого равен \( a\). Кубический корень определен для всех \( a\). Его можно извлечь из любого числа: \( \sqrt[3]{-27}=-3\). Как видим, он может принимать и отрицательные значения.
Корень \( n\)-ой степени из числа \( a\) — это число, \( n\)-я степень которого равна \( a\), т.е.
\( c=\sqrt[n]{a}\Leftrightarrow {{c}^{n}}=a\)
Если \( n\) — чётно, тогда:
- если \( a<0\), то корень \( n\)-ой степени из a не определен.
- если \( a\ge 0\), то неотрицательный корень уравнения \( {{x}^{n}}=a\) называется арифметическим корнем \( n\)-ой степени из \( a\) и обозначается \( \sqrt[n]{a}\).
Если \( n\) — нечётно, тогда уравнение \( {{x}^{n}}=a\) имеет единственный корень при любом \( a\).
Ты заметил, что слева сверху от знака корня мы пишем его степень? Но только не для квадратного корня! Если видишь корень без степени, значит он квадратный (степени \( \displaystyle 2\)).
Примеры:
- \( \sqrt[4]{10000}=10\)
- \( \sqrt[5]{-243}=-3\)
- \( \sqrt[7]{128}=2\)
Основные свойства корней
Для любого натурального \( n\), целого \( k\) и любых неотрицательных чисел \( a\) и \( b\) выполнены равенства:
| \( \sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b};\) |
| \( \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\text{ }\left( b\ne 0 \right);\) |
| \( \sqrt[n]{\sqrt[k]{a}}=\sqrt[nk]{a}\text{ }\left( k>0 \right);\) |
| \( \sqrt[nk]{{{a}^{k}}}=\sqrt[n]{a}\text{ }\left( k>0 \right);\) |
| при нечетных \( n\): \( \sqrt[n]{{{a}^{k}}}={{\left( \sqrt[n]{a} \right)}^{k}}\text{ }\left( \text{если }k\le 0,\text{ }то\text{ }a\ne 0 \right)\) |
| при четных \( k\) и \( n\): \( \sqrt[n]{{{a}^{k}}}={{\left( \sqrt[n]{\left| a \right|} \right)}^{k}}\text{ }\left( \text{если }k\le 0,\text{ то }a\ne 0 \right)\) |
Подготовка к ЕГЭ на 90+ в мини-группах
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Спасибо огромное) Всё понятно и помогло мне при подготовке к контрольной)
Поля! Спасибо! Ты — крутышка! 🙂
Некоторые комментарии прошлых лет к этой статье:
Айдар
22 июня 2018
Это прекрасно! Я в восторге
Александр (админ)
22 июня 2018
Спасибо, Айдар! Делитесь с друзьями, если понравился учебник! Будем признательны.
Мария
12 марта 2020
Воу, спасибо вам. Я сейчас в 7 классе и вы мне оооочень помогли с этой темой, раньше я её не очень понимала, но сейчас вроде бы щёлкаю как орешки))))) Спасибо вам большое
Александр (админ)
12 марта 2020
Мария, ты крутышка! Не все могут разобраться даже имея хороший материал под рукой. А ты это сделала. Молодец!