Решение логарифмических уравнений на ЕГЭ
Сегодня в этой статье мы с тобой обсудим, как решать простые и сложные логарифмические уравнения.
Для этого тебе понадобятся некоторые минимальные знания:
- Свойства логарифмов
- Свойства степени
- Формулы сокращенного умножения
- Решение линейных и квадратных уравнений.
Обрати внимание: статья написана для учеников разного уровня подготовки, от ничего не знающих до суперпродвинутых.
Знаний, полученных в этой статье с лихвой хватит, чтобы решить любую задачу ЕГЭ по этой теме.
Логарифмические уравнения — коротко о главном
Определение логарифмических уравнений
Логарифмическое уравнение — уравнение, в котором неизвестные переменные находятся внутри логарифмов.
Простейшим логарифмическим уравнением является уравнение вида \( \displaystyle lo{{g}_{a}}~x~=~b\).
Процесс решения любого логарифмического уравнения сводится к приведению логарифмического уравнения к виду \( \displaystyle lo{{g}_{a}}\left( f\left( x \right) \right)~=~lo{{g}_{a}}\left( g\left( x \right) \right)\), и переходе от уравнения с логарифмами к уравнению без них: \( \displaystyle f\left( x \right)=g\left( x \right)\).
ОДЗ (Область допустимых значений) для логарифмического уравнения:
\( \displaystyle \left\{ \begin{align}& f(x)>0,\\ & a>0,\text{}\\& a\ne 1.\\\end{align}\right.\)5 основных методов решения логарифмических уравнений:
1 метод. Использование определения логарифма:
\( \displaystyle lo{{g}_{a}}~f(x)=b\ \Leftrightarrow \ ~f(x)={{a}^{b}},\ \ \ a>0,\ a\ne 1\).
2 метод. Использование свойств логарифма:
- \( \displaystyle lo{{g}_{{{a}^{c}}}}b=\frac{1}{c}lo{{g}_{a}}b\)
- \( \displaystyle c\cdot lo{{g}_{a}}b=lo{{g}_{a}}{{b}^{c}}\)
- \( \displaystyle lo{{g}_{a}}b+lo{{g}_{a}}c=lo{{g}_{a}}\left( bc \right)\)
- \( \displaystyle lo{{g}_{a}}b-lo{{g}_{a}}c=lo{{g}_{a}}\left( \frac{b}{c} \right)\)
- \( \displaystyle {{\log }_{{{a}^{n}}}}b=\frac{1}{n}\cdot {{\log }_{a}}b\)
- \( \displaystyle {{\log }_{{{a}^{n}}}}{{b}^{m}}=\frac{m}{n}\cdot {{\log }_{a}}b\)
- \( \displaystyle lo{{g}_{a}}1=0,~a>0,a\ne 1\)
- \( \displaystyle lo{{g}_{a}}a=1~(a>0,a\ne 1)\)
3 метод. Введение новой переменной (замена):
Замена \( \displaystyle lo{{g}_{a}}x~=~t\)позволяетсвести логарифмическое уравнение к более простому алгебраическому уравнению относительно t.
4 метод. Переход к новому основанию:
\( \displaystyle {{\log }_{a}}b=\frac{{{\log }_{c}}b}{{{\log }_{c}}a}\text{ }\left( c>0;\text{ }\ne \text{1} \right)\).
\( \displaystyle {{\log }_{a}}b=\frac{1}{{{\log }_{b}}a},\text{ }\left( b\ne 1 \right)\).
5 метод. Логарифмирование:
Берется логарифм от правой и левой частей уравнения.
Теорема: Если \( \displaystyle a>1\), то функция \( \displaystyle f(x)=lo{{g}_{a}}x\) является монотонно возрастающей, если \( \displaystyle 0<a<1\), то функция\( \displaystyle f(x)=lo{{g}_{a}}x\) является монотонно убывающей.
\( \displaystyle \left\{ \begin{array}{l}f\left( x \right)=g\left( x \right)\\f\left( x \right)\ge A\\g\left( x \right)\le A\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}f\left( x \right)=A\\g\left( x \right)=A\end{array} \right.\).
Что такое логарифмические уравнения
Это уравнения, в которых неизвестные переменные (ну мы такие жуткие случаи, когда переменных несколько, рассматривать не будем, для нас переменная всегда будет одна и называть мы ее будем «икс») находятся внутри логарифмов.
Например:
- \(\displaystyle lo{{g}_{5}}\left( {{x}^{2}}+2x \right)=lo{{g}_{5}}\left( {{x}^{2}}+10 \right)\)
- \(\displaystyle lo{{g}_{5}}\left( 5-x \right)=2lo{{g}_{5}}3\)
- \(\displaystyle {{3}^{lo{{g}_{9}}\left( 5{x} -5 \right)}}=5\)
- \(\displaystyle lo{{g}_{{x} -1}}8=1\)
А вот уравнение \(\displaystyle 1+2x=lo{{g}_{2}}\left( 3x+1 \right)\) нельзя называть логарифмическим.
Я думаю, тебе вполне ясно, почему?
Верно, все потому, что \(\displaystyle 2x\) не находится внутри никакого логарифма.
Такие уравнения называются смешанными и требуют индивидуального подхода.
Как же решать логарифмические уравнения?
3 основных способа решения логарифмических уравнений
На самом деле существует целая масса подходов: это и разложение на множители, и потенцирование, и замена, и работа с основаниями…
Но все методы решения логарифмических уравнения роднит одно: их цель свести логарифмические уравнения к простейшему виду:
\( lo{{g}_{a}}\left( f\left( x \right) \right)~=~lo{{g}_{a}}\left( g\left( x \right) \right)\),
а затем уже решать уравнение без логарифмов:
\( f\left( x \right)=g\left( x \right).\)
То есть правило такое:
Если уравнение сведено к такому, что слева и справа от знака «равно» стоят логарифмы с одним основанием, то логарифмы мы «зачеркиваем» и решаем оставшееся уравнение.
Однако, тут есть один подводный камень: поскольку логарифм \( lo{{g}_{a}}\left( f\left( x \right) \right)\) определен только тогда, когда
\( f\left( x \right)>0,\)
то после нахождения корней логарифмического уравнения, мы обязаны сделать проверку!!! Я не поленюсь и повторю еще раз:
В логарифмических уравнениях мы всегда делаем проверку получения корней!!!
Те учащиеся, которые игнорируют это требование, как правило допускают глупейшие и непростительные ошибки.
Cогласись, обидно решить правильно уравнение, а потом не сделать самую малость: проверку, и записать лишние корни, и записать из-за этого неправильный ответ!
Теперь давай потренируемся на решении простейших примеров (все примеры взяты из банка задач ЕГЭ), чтобы понять 6 основных способов решения логарифмических уравнений.
Примеры
- \( lo{{g}_{2}}\left( 4-x \right)=7\)
- \( lo{{g}_{5}}\left( 4+x \right)=2\)
- \( lo{{g}_{2}}\left( 15+x \right)=lo{{g}_{2}}3~\)
- \( lo{{g}_{\frac{1}{7}}}\left( 7-x \right)=-2~\)
- \( lo{{g}_{5}}\left( 7-x \right)=lo{{g}_{5}}\left( 3-x \right)+1\)
- \( lo{{g}_{8}}{{2}^{8{x} -4}}=4\)
Давай разбираться с каждым способом и примером по-отдельности.
Способ 1. Правило умножения на единицу
Пример №1
\( lo{{g}_{2}}\left( 4-x \right)=7\)Слева у нас стоит выражение с логарифмом, а справа – нет.
Что делать?
Нужно сделать так, чтобы справа тоже было выражение с логарифмом по основанию \( \displaystyle 2\), а затем просто откинуть логарифмы.
Как этого добиться? Я люблю применять волшебное правило:
Правило умножения на единицу!
Вот в чем его соль: я умножу \( \displaystyle 7\) на \( \displaystyle 1\)
\( \displaystyle 7\cdot 1\)
Однако, мне же нужен логарифм! Что я знаю:
\( \displaystyle lo{{g}_{a}}a=1~(a>0,a\ne 1)\)
Мне же нужно основание \( \displaystyle 2\), поэтому я возьму \( \displaystyle a=2\), тогда
\( \displaystyle 1=lo{{g}_{2}}2\)
\( \displaystyle 7=7\cdot 1=7\cdot ~lo{{g}_{2}}2\)
Полдела сделано! Теперь мне нужно засунуть \( \displaystyle 7\) внутрь логарифма.
Это я сделаю, воспользовавшись следующим правилом:
\( \displaystyle c\cdot lo{{g}_{a}}b=lo{{g}_{a}}{{b}^{c}}\)
Применительно к моей ситуации это даст:
\( \displaystyle 7\cdot ~lo{{g}_{2}}2=lo{{g}_{2}}{{2}^{7}}=lo{{g}_{2}}128\)
Тогда мое исходное логарифмическое уравнение станет вот таким:
\( \displaystyle lo{{g}_{2}}\left( 4-x \right)=lo{{g}_{2}}128\)
Ура! Избавляемся от логарифмов! Получим простейшее уравнение:
\( \displaystyle 4-x=128,\)
\( \displaystyle x=-124\)
Но это еще не конец! Обещанная проверка:
Пример №2
\( lo{{g}_{5}}\left( 4+x \right)=2\)Задача полностью аналогичная предыдущей: воспользуюсь правилом умножения на единицу для числа \( 2\):
\( 2=2\cdot ~lo{{g}_{5}}5=lo{{g}_{5}}{{5}^{2}}=lo{{g}_{5}}25\)
Тогда исходное уравнение станет вот таким:
\( lo{{g}_{5}}\left( 4+x \right)=lo{{g}_{5}}25.\)
Зачеркиваем логарифмы:
\( 4+x=25,\)
\( x=21.\)
Делаем проверку:
\( lo{{g}_{5}}\left( 4+21 \right)=2\)
\( lo{{g}_{5}}25=2\)
Верно!
Пример №3
\( lo{{g}_{2}}\left( 15+x \right)=lo{{g}_{2}}3~\)А здесь о нас с тобой уже заранее позаботились! Зачеркиваем логарифмы и получим:
\( 15+x=3,\)
\( x=-12\)
Делаем проверку:
\( lo{{g}_{2}}\left( 15-12 \right)=lo{{g}_{2}}3\)
\( lo{{g}_{2}}3=lo{{g}_{2}}3\)
Все верно!
Пример №4
\( lo{{g}_{\frac{1}{7}}}\left( 7-x \right)=-2\)Опять воспользуемся волшебным правилом!
Способ 2. Правило «превращения единицы»
Разберем это правило на пятом примере логарифмического уравнения:
Пример № 5
\( lo{{g}_{5}}\left( 7-x \right)=\text{ }\!\!~\!\!\text{ }lo{{g}_{5}}\left( 3-x \right)+1\)Воспользуемся правилом «превращения единицы», которым мы уже пользовались в правиле «умножения на единицу»! Смотри как оно работает:
\( 1=lo{{g}_{5}}5\)
Тогда исходное уравнение станет вот таким:
\( lo{{g}_{5}}\left( 7-x \right)=\text{ }\!\!~\!\!\text{ }lo{{g}_{5}}\left( 3-x \right)+lo{{g}_{5}}5\)
Что дальше? Если ты видишь с одной стороны уравнения сумму (или разность, но лучше сумму!) логарифмов с одним основанием, то пользуйся вот такой формулой (тебе уже известной!)
\( lo{{g}_{a}}b+lo{{g}_{a}}c=lo{{g}_{a}}\left( bc \right)\)
Применительно к моей ситуации это даст:
\( lo{{g}_{5}}\left( 7-x \right)=\text{ }\!\!~\!\!\text{ }lo{{g}_{5}}5\left( 3-x \right)\)
Ну все, слева и справа у нас – логарифмы и ничего более. Убираем их.
\( 7-x=5\left( 3-x \right)\)
\( 7-x=15-5x\)
\( 4x=8\)
\( x=2.\)
Проверка:
\( lo{{g}_{5}}\left( 7-2 \right)=lo{{g}_{5}}\left( 3-2 \right)+1\)
\( lo{{g}_{5}}5=lo{{g}_{5}}1+1\)
\( 1=0+1\)
\( 1=1\)
Верно!
Кстати, а ты понял, откуда у нас взялся ноль справа? Ты асболютно прав:
\( lo{{g}_{a}}1=0,~a>0,a\ne 1.\)
Способ 3. Использование свойств логарифма
Пример № 6
\( lo{{g}_{8}}{{2}^{8{x} -4}}=4\)Здесь у нас есть два возможных пути:
Первый – это как всегда правило умножения на единицу (ты можешь попытаться его проделать самостоятельно, ты ведь знаешь, как решать показательные уравнения?),
Второй – воспользоваться одним из свойств логарифма:
\( c\cdot lo{{g}_{a}}b=lo{{g}_{a}}{{b}^{c}}\)
Но читать я ее буду справа налево:
\( lo{{g}_{8}}{{2}^{8{x} -4}}=\left( 8{x} -4 \right)lo{{g}_{8}}2\)
Теперь разберемся с числом
\( lo{{g}_{8}}2\)
Здесь нам понадобится еще одно хорошо известное тебе свойство:
\( lo{{g}_{{{a}^{c}}}}b=\frac{1}{c}lo{{g}_{a}}b\)
Что она даст в нашем случае? Так как \( \displaystyle 8={{2}^{3}}\), то
\( \displaystyle lo{{g}_{8}}2=lo{{g}_{{{2}^{3}}}}2=\frac{1}{3}lo{{g}_{2}}2=\frac{1}{3}\cdot 1=\frac{1}{3}\)
Тогда левая часть уравнения примет вид:
\( \displaystyle \frac{1}{3}\cdot \left( 8{x} -4 \right)=4\)
\( \displaystyle 8{x} -4=12\)
\( \displaystyle 8x=16\)
\( \displaystyle x=2.\)
Проверка!
\( \displaystyle lo{{g}_{8}}{{2}^{8\cdot 2-4}}=4\)
\( \displaystyle lo{{g}_{8}}{{2}^{12}}=4\)
\( \displaystyle lo{{g}_{8}}{{2}^{3\cdot 4}}=4\)
\( \displaystyle lo{{g}_{8}}{{8}^{4}}=4\)
\( \displaystyle 4lo{{g}_{8}}8=4\)
\( \displaystyle 4=4.\)
Все верно!
Ну что же, во всех предыдущих примерах, так уж выходило (абсолютно случайно, кстати), что логарифмические уравнения имели корни, притом единственные, и все они нам подходили.
Так бывает далеко не всегда, увы! Но прежде чем я приведу тебе соответствующие примеры, я еще раз хочу напомнить тебе, какие формулы очень нужны для решения логарифмических уравнений:
6 главных формул необходимых для решения логарифмических уравнений:
- \( lo{{g}_{{{a}^{c}}}}b=\frac{1}{c}lo{{g}_{a}}b\)
- \( c\cdot lo{{g}_{a}}b=lo{{g}_{a}}{{b}^{c}}\)
- \( lo{{g}_{a}}b+lo{{g}_{a}}c=lo{{g}_{a}}\left( bc \right)\)
- \( lo{{g}_{a}}b-lo{{g}_{a}}c=lo{{g}_{a}}\left( \frac{b}{c} \right)\)
- \( lo{{g}_{a}}1=0,~a>0,a\ne 1.\)
- \( lo{{g}_{a}}a=1~(a>0,a\ne 1)\)
Не так уж и много, правда?
Но тем не менее, эти формулы нам ЖИЗНЕННО НЕОБХОДИМЫ! Без них мы не сможем решить даже простейший пример.
Ну а далее обещанные примеры, где все не очень хорошо с корнями!
- \( \displaystyle lo{{g}_{4}}\frac{{{x}^{2}}-4x+1}{{{x}^{2}}-6x+5}=-\frac{1}{2}\)
- \( \displaystyle lo{{g}_{5}}\left( 3{x} -11 \right)+lo{{g}_{5}}\left( {x} -27 \right)=lo{{g}_{5}}8+3\)
- \( \displaystyle lg({x} -3)+lg({x} -2)=1-lg5\)
А теперь разбираем!
Я надеюсь, что только что приведенные примеры навсегда отучат тебя пропускать проверку при решении логарифмических уравнений. Она необходима!
Логарифмическое уравнение с переменным основанием
Теперь я бы хотел рассмотреть с тобой еще один (чуть более сложный) вид логарифмических уравнений. Это будут уравнения с переменным основанием.
До этого же мы рассматривали только случаи, когда основания были постоянными: \( \displaystyle 2,3,10\) и т. д. Но ничто не мешает им быть некоторыми функциями от \( \displaystyle x\), например \( \displaystyle 2x+1,~{{x}^{2}},~{{2}^{x}}\) и т. д.
Но не стоит пугаться!
Если при решении логарифмических неравенств переменное основание доставляет довольно много неудобств, то на сложности решения уравнения это практически никак не сказывается.
Пример №1
\( \displaystyle log{{~}_{{x} -1}}25~=~2.\)
Действуем как и раньше: применяем метод «умножь на единицу» к числу \( \displaystyle 2\):
\( \displaystyle 2=2\cdot lo{{g}_{{x} -1}}\left( {x} -1 \right)=lo{{g}_{{x} -1}}{{\left( {x} -1 \right)}^{2}}\)
Тогда исходное уравнение преобразуется к виду:
\( \displaystyle 25={{\left( {x} -1 \right)}^{2}}\)
\( \displaystyle {{\left( {x} -1 \right)}^{2}}-25=0\)
Применю формулу разности квадратов:
Как видишь, в случае уравнений нет никакой принципиальной разницы, переменные у нас основания или нет. В этом плане можно сказать, что решить логарифмическое уравнение как правило намного проще, чем решить логарифмическое неравенство!
Давай теперь попробуем решить еще вот такой «странный» пример.
Пример №2
\( \displaystyle lo{{g}_{lo{{g}_{3}}x}}3=2\)
Будем действовать как всегда – превратим правую часть в логарифм, вот такой хитрый:
\( \displaystyle 2=2\cdot lo{{g}_{lo{{g}_{3}}x}}\left( lo{{g}_{3}}x \right)=lo{{g}_{lo{{g}_{3}}x}}{{\left( lo{{g}_{3}}x \right)}^{2}}\)
Тогда исходное логарифмическое уравнение будет равносильно вот такому уравнению (правда снова логарифмическому):
\( \displaystyle {{\left( lo{{g}_{3}}x \right)}^{2}}=3\)
Данное уравнение я буду решать снова по разности квадратов:
Я намеренно привел достаточно сложный пример, чтобы показать тебе, что не стоит пугаться больших и страшных логарифмов: достаточно знать несколько формул (которые я уже привел тебе выше) и из любой (практически) ситуации можно найти выход.
Ну вот, я привел тебе основные методы решения логарифмических уравнений (методы «без изысков»), которые позволят тебе справиться с большинством примеров ( в первую очередь на ЕГЭ). Теперь пришло твое время показать, чему ты научился. Попробуй самостоятельно решить следующие логарифмические уравнения, а затем мы с тобой сверим результат.
А теперь попробуй порешать логарифмические уравнения самостоятельно:
Разбор 7 примеров решения логарифмических уравнений
- \( \displaystyle lo{{g}_{3}}{x} -2lo{{g}_{\frac{1}{3}}}x=6\)
- \( \displaystyle \lg \left( {{x}^{2}}+2{x} -7 \right)-\lg \left( {x} -1 \right)=0\)
- \( \displaystyle lo{{g}_{25}}x+lo{{g}_{5}}x=lo{{g}_{\frac{1}{5}}}\sqrt{8}\)
- \( \displaystyle lo{{g}_{2}}\left( 2\sqrt{x+5}+5 \right)+lo{{g}_{0.5}}\left( -{x} -0.5 \right)=1\)
- \( \displaystyle lo{{g}_{7x}}2+lo{{g}_{7x}}4+lo{{g}_{7x}}5=lo{{g}_{7x}}\left( x+33 \right)\)
- \( \displaystyle lo{{g}_{3x+8}}\left( 2{{x}^{2}}+3 \right)=lo{{g}_{3x+8}}35\)
- \( \displaystyle lo{{g}_{{{x}^{2}}+5x+7}}lo{{g}_{{x} -4}}3x=0\)
Рассмотренные в этой работы приемы, конечно, не исчерпывают всевозможные способы решения логарифмических уравнений. В некоторых случаях нам нужно очень «извернуться», чтобы придумать способ найти корни у каверзного уравнения.
Однако, каким бы сложным не было начальное уравнение, в результате оно сведется к уравнению того вида, которые мы с тобой только что научились решать!
Ответы на примеры для самостоятельной работы
1. \( \displaystyle lo{{g}_{3}}{x} -2lo{{g}_{\frac{1}{3}}}x=6\)
Достаточно простая задачка. Воспользуемся свойством:
\( \displaystyle lo{{g}_{{{a}^{c}}}}b=\frac{1}{c}lo{{g}_{a}}b\)
В вычитаемом:
\( \displaystyle -2lo{{g}_{\frac{1}{3}}}x=-2lo{{g}_{{{3}^{-1}}}}x=\frac{-2}{-1}lo{{g}_{3}}x=2lo{{g}_{3}}x\)
Тогда мы получим:
2. \( \displaystyle \lg \left( {{x}^{2}}+2{x} -7 \right)-\lg \left( {x} -1 \right)=0\)
Тоже ничего сверхъестественного: неохота мне делить, поэтому я перенесу слагаемое с «минусом» вправо: теперь слева и справа у меня стоят десятичные логарифмы, и я от них избавляюсь:
\( \displaystyle {{x}^{2}}+2{x} -7={x} -1\)
\( \displaystyle {{x}^{2}}+{x} -6=0\)
\( \displaystyle {{x}_{1}}=-3,{{x}_{2}}=2\)
Делаю проверку:
3. \( \displaystyle lo{{g}_{25}}x+lo{{g}_{5}}x=lo{{g}_{\frac{1}{5}}}\sqrt{8}\)
Здесь нужно немного поработать: ясно, что \( \displaystyle 25={{5}^{2}},~\frac{1}{5}={{5}^{-1}}\), снова воспользуюсь (не правда ли очень полезной?) формулой:
\( \displaystyle lo{{g}_{{{a}^{c}}}}b=\frac{1}{c}lo{{g}_{a}}b\)
\( \displaystyle 0.5lo{{g}_{5}}x+lo{{g}_{5}}x=-lo{{g}_{5}}\sqrt{8}\)
\( \displaystyle 1.5lo{{g}_{5}}x+lo{{g}_{5}}\sqrt{8}=0\)
Что мне нужно сделать, прежде чем применить формулу сложения логарифмов?
Да, мне нужно избавиться от множителя \( \displaystyle 1.5\). Есть два пути: первый – в лоб занести его в логарифм по формуле:
\( \displaystyle c\cdot lo{{g}_{a}}b=lo{{g}_{a}}{{b}^{c}}\)
В принципе, этот метод имеет право на существование, но что в нем плохо? Плохо иметь дело с выражением вида \( \displaystyle {{x}^{1.5}}\) (всегда неприятна «нецелая степень».
Так что можно сделать еще? Как можно избавиться от такой «нецелости»?
4. \( \displaystyle lo{{g}_{2}}\left( 2\sqrt{x+5}+5 \right)+lo{{g}_{0.5}}\left( -{x} -0.5 \right)=1\)
Как и в предыдущем примере перепишем
\( \displaystyle lo{{g}_{0.5}}\left( -{x} -0,5 \right)\) в виде:
\( \displaystyle -lo{{g}_{2}}\left( -{x} -0,5 \right)\)
Я опять не хочу никаких вычитаний ( и последующих делений) и поэтому перенесу полученное выражение вправо:
\( \displaystyle 1+lo{{g}_{2}}\left( -{x} -0,5 \right)=lo{{g}_{2}}2+~lo{{g}_{2}}\left( -{x} -0,5 \right)=lo{{g}_{2}}\left( -2{x} -1 \right)\)
Теперь убираю логарифмы слева и справа:
\( \displaystyle 2\sqrt{x+5}+5=-2{x} -1\)
\( \displaystyle 2\sqrt{x+5}=-2{x} -1-5\)
\( \displaystyle 2\sqrt{x+5}=-2{x} -6\)
\( \displaystyle \sqrt{x+5}=-{x} -3\)
Мы получили иррациональное уравнение, которое, как я надеюсь, ты уже умеешь решать. Я лишь напомню, что мы возводим обе стороны в квадрат:
5. \( \displaystyle lo{{g}_{7x}}2+lo{{g}_{7x}}4+lo{{g}_{7x}}5=lo{{g}_{7x}}\left( x+33 \right).\)
Все прозрачно: применяем формулу суммы логарифмов слева:
\( \displaystyle lo{{g}_{7x}}2+lo{{g}_{7x}}4+lo{{g}_{7x}}5=lo{{g}_{7x}}2\cdot 4\cdot 5=lo{{g}_{7x}}40\)
Тогда убираем логарифмы с двух сторон:
\( \displaystyle 40=x+33\)
\( \displaystyle x=7\)
Проверка:
\( \displaystyle lo{{g}_{49}}40=lo{{g}_{49}}40\)
Верно!
Ответ: \( \displaystyle x=7\);
6. \( \displaystyle lo{{g}_{3x+8}}\left( 2{{x}^{2}}+3 \right)=lo{{g}_{3x+8}}35.\)
Все проще некуда: уравнение уже приведено к простейшему виду. Нам осталось только приравнять
\( \displaystyle 2{{x}^{2}}+3=35\)
\( \displaystyle 2{{x}^{2}}-32=0\)-32=0
\( \displaystyle {{x}^{2}}-16=0\)
Опять воспользуемся формулой разности квадратов. Она позволяет при решении уравнений вида \( \displaystyle a{{x}^{2}}=b~\) не терять корни!
7. \( \displaystyle lo{{g}_{{{x}^{2}}+5x+7}}lo{{g}_{{x}^{2} -4}}3x=0\)
Этот пример я оставил нам на десерт. Хотя в нем тоже нет ничего очень уж сложного.
Ноль представим как
\( \displaystyle 0=lo{{g}_{{{x}^{2}}+5x+7}}1\)
Тогда мы с тобой получим вот такое логарифмическое уравнение:
\( \displaystyle lo{{g}_{{{x}^{2}}+5x+7}}lo{{g}_{{{x}^{2}}-4}}3x=lo{{g}_{{{x}^{2}}+5x+7}}1\)
И мы снимаем первую «шкурку» — внешние логарифмы.
\( \displaystyle lo{{g}_{{{x}^{2}}-4}}3x=1\)
Единицу представим как
\( \displaystyle 1=lo{{g}_{{{x}^{2}}-4}}\left( {{x}^{2}}-4 \right)\)
Тогда наше уравнение примет вид:
\( \displaystyle lo{{g}_{{{x}^{2}}-4}}3x=lo{{g}_{{{x}^{2}}-4}}\left( {{x}^{2}}-4 \right)\)
Теперь мы снимаем «вторую шкурку» и добираемся до сердцевины:
\( \displaystyle 3x={{x}^{2}}-4\)
\( \displaystyle {{x}_{1}}=4,~{{x}_{2}}=-1\)
Делаем проверку:
\( \displaystyle x=4\):
\( \displaystyle lo{{g}_{{{4}^{2}}+5\cdot 4+7}}lo{{g}_{{{4}^{2}}-4}}3\cdot 4=0\)
\( \displaystyle lo{{g}_{42}}lo{{g}_{12}}12=0\)
\( \displaystyle lo{{g}_{42}}1=0\)
\( \displaystyle 0=0\).
Верно!
\( \displaystyle x=-1\)
\( \displaystyle lo{{g}_{{{\left( -1 \right)}^{2}}+5\cdot \left( -1 \right)+7}}lo{{g}_{{{\left( -1 \right)}^{2}}-4}}3\cdot \left( -1 \right)=0\)
Неверно!
Ответ: \( \displaystyle x=4\).
Четыре продвинутых метода решения логарифмических уравнений
Теперь, после ознакомления с логарифмическими уравнениями, ты овладел необходимым минимумом знаний, необходимых для решения простейших примеров.
Теперь я могу перейти к разбору четырех продвинутых методов решения логарифмических уравнений:
- метод введения новой переменной (или замены)
- метод логарифмирования
- метод перехода к новому основанию
- мини-максный метод
Метод введения новой переменной (или замены) – один из наиболее часто употребляемых на практике. Им решается большинство «трудных» задач, связанных с решением логарифмических (и не только) уравнений.
Метод логарифмирования служит для решения смешанных показательно-логарифмических уравнений, в конечном счете сводя задачу к выбору хорошей замены переменной ( то есть к первому методу).
Метод перехода к новому основанию пригоден для решения некоторых уравнений, в которых встречаются логарифмы с разными основаниями.
Мини-максный метод применяется для решения уравнений, которые не могут быть решены методом логарифмирования обеих частей.
Метод введения новой переменной
Я начну с рассмотрения первого метода. Как ты уже понял из названия, суть этого метода – ввести такую замену переменной, что твое логарифмическое уравнение чудесным образом преобразится в такое, которое ты уже с легкостью можешь решить.
Все что тебе останется после решения этого самого «упрощенного уравнения» — это сделать «обратную замену» : то есть вернуться от замененного к заменяемому. Давай проиллюстрируем только что сказанное на очень простом примере:
\( \displaystyle \frac{1}{4-lgx}+\frac{2}{2+lgx}=1\)
В этом примере замена прямо напрашивается сама собой! Ведь ясно, что если мы заменим \( \displaystyle lgx\) на \( \displaystyle t\), то наше логарифмическое уравнение превратится в рациональное:
\( \displaystyle \frac{1}{4-t}+\frac{2}{2+t}=1\)
Его ты без проблем решишь, сведя к квадратному:
\( \displaystyle \left( 2+t \right)+2\left( 4-t \right)=\left( 4-t \right)\left( 2+t \right)\)
\( \displaystyle t\ne 4,t\ne -2\) (дабы знаменатель не обнулился ненароком!)
Упрощая полученное выражение, мы окончательно получим:
\( \displaystyle {{t}^{2}}-3t+2=0\)
\( \displaystyle {{t}_{1}}=1,{{t}_{2}}=2\)
Теперь делаем обратную замену: \( \displaystyle t=lgx\), тогда из \( \displaystyle 1=lgx\) следует, что \( \displaystyle x=10\), а из \( \displaystyle 2=lgx\) получим \( \displaystyle x=100\)
Теперь, как и раньше, пришла очередь проверки:
Пусть вначале \( \displaystyle x=10\), так как \( \displaystyle \lg 10=1\), то \( \displaystyle \frac{1}{4-1}+\frac{2}{2+1}=\frac{1}{3}+\frac{2}{3}=1\), верно!
Теперь \( \displaystyle x=100,\lg 100=2\), тогда \( \displaystyle \frac{1}{4-2}+\frac{2}{2+2}=\frac{1}{2}+\frac{2}{4}=1\), все верно!
Таким образом, числа \( \displaystyle 10\) и \( \displaystyle 100\) являются корнями нашего исходного уравнения.
Ответ: \( \displaystyle 10,100\).
Вот еще один пример с очевидной заменой:
1. \( \displaystyle 3\log _{2}^{2}x-7{{\log }_{2}}x+2=0\)
В самом деле, сразу же давай заменим
\( \displaystyle t={{\log }_{2}}x\)
Тогда наше исходное логарифмическое уравнение превратится в квадратное:
\( \displaystyle 3{{t}^{2}}-7t+2=0\)
\( \displaystyle {{t}_{1}}=2,{{t}_{2}}=\frac{1}{3}\)
Обратная замена:
\( \displaystyle 2={{\log }_{2}}x\), откуда \( \displaystyle x=4\), \( \displaystyle \frac{1}{3}={{\log }_{2}}x,x={{2}^{\frac{1}{3}}}\)
Проверку проведи самостоятельно, убедись, что в данном случае оба найденных нами числа являются корнями.
Мне кажется, что основную идею ты уловил. Она не нова и распространяется не только на логарифмические уравнения.
Другое дело, что иногда довольно сложно сразу «увидеть» замену. Здесь требуется некоторый опыт, который придет к тебе после некоторых усилий с твоей стороны.
А пока что потренируйся в решении следующих примеров:
2. \( \displaystyle \frac{{{\log }_{2}}\frac{x}{2}}{{{\log }_{2}}x}-\frac{{{\log }_{2}}{{x}^{2}}}{{{\log }_{2}}x-1}=1\)
3. \( \displaystyle 0.1{{\lg }^{4}}x-{{\lg }^{2}}x+0,9=0.\)
Готов? Давай проверим, что у тебя получилось:
Вначале решим второй пример.
Он как раз демонстрирует тебе, что не всегда замену удается сделать, что говорится, «в лоб». Прежде нам нужно немного преобразовать наше уравнение: применить формулу разности логарифмов в числителе первой дроби, и вынести степень в числителе второй.
Сделав это, ты получишь:
\( \displaystyle \frac{{{\log }_{2}}x-1}{{{\log }_{2}}x}-\frac{2{{\log }_{2}}x}{{{\log }_{2}}x-1}=1\)
Теперь замена стала очевидной, не так ли?
Давай сделаем ее: \( \displaystyle t=lo{{g}_{2}}x\). Теперь приведем дроби к общему знаменателю и упростим. Тогда мы получим:
\( \displaystyle \frac{{{\left( t-1 \right)}^{2}}-2{{t}^{2}}}{t\left( t-1 \right)}=\frac{t\left( t-1 \right)}{t\left( t-1 \right)}\)
или
\( \displaystyle 2{{t}^{2}}+t-1=0\)
при \( \displaystyle t\ne 1,t\ne 0.\)
Решив последнее уравнение, ты найдешь его корни:
\( \displaystyle {{t}_{1}}=-1,{{t}_{2}}=0.5\) откуда \( \displaystyle {{x}_{1}}=\frac{1}{2},{{x}_{2}}=\sqrt{2}\).
Самостоятельно сделай проверку и удостоверься в том, что \( \displaystyle {{x}_{1}}\) и \( \displaystyle {{x}_{2}}\) в самом деле являются корнями нашего первоначального уравнения.
Теперь давай попробуем решить третье уравнение
Метод перехода к новому основанию
Давай рассмотрим следующее уравнение:
\( \displaystyle 2{{\log }_{5}}x+2{{\log }_{x}}5=5\)
Что мы видим? Два логарифма будто бы «противоположны» друг другу. Что нужно делать? Все легко: нам достаточно прибегнуть к одной из двух формул:
\( \displaystyle {{\log }_{a}}b=\frac{1}{{{\log }_{b}}a}\) или \( \displaystyle {{\log }_{a}}b=\frac{{{\log }_{c}}b}{{{\log }_{c}}a}\) \( \displaystyle (для\ любого\ c>0,c\ne 1)\)
В принципе, мне ничего не мешает воспользоваться любой из этих двух формул, но из-за структуры уравнения, мне удобнее будет применить первую: я избавлюсь от переменного основания логарифма во втором слагаемом, заменив его на \( \displaystyle \frac{1}{{{\log }_{5}}x}\).
Теперь легко заметить, что задача свелась к предыдущей: к выбору замены. Заменив \( \displaystyle t={{\log }_{5}}x\), я получу следующее уравнение:
\( \displaystyle 2t+\frac{2}{t}=5\)
или
(при \( \displaystyle t\ne 0\))
\( \displaystyle 2{{t}^{2}}-5t+2=0\)
\( \displaystyle {{t}_{1}}=2,{{t}_{2}}=0.5\)
Отсюда \( \displaystyle {{x}_{1}}=25,{{x}_{2}}=\sqrt{5}\). Тебе осталось подставить найденные числа в исходное уравнение и убедиться, что они в самом деле являются корнями.
Вот еще один пример, в котором разумно будет перейти к новому основанию:
\( \displaystyle \log_{{x}^{2}}{16}+\log_{2x}{64}=3\)
Однако, как ты можешь легко проверить, если мы с тобой перейдем к новому основанию сразу, это не даст должного эффекта. Что нам нужно сделать в этом случае?
А давай все упростим донельзя, а дальше будь что будет.
Вот, что я хочу сделать: представить \( \displaystyle 16\), как \( \displaystyle {{2}^{4}}\), \( \displaystyle 64\) как \( \displaystyle {{2}^{6}}\), вынести эти степени перед логарифмами, а также вынести квадрат у икса в первом логарифме. Дальше уже посмотрим.
\( \displaystyle 4\cdot \left( 0.5 \right)\cdot {{\log }_{x}}2+6{{\log }_{2x}}2=3[/latex[latex] \displaystyle 2{{\log }_{x}}2+6{{\log }_{2x}}2=3\)
Что делать дальше?
Есть негласное правило: делай основание логарифма как можно проще!
Запомни, с основанием бывает намного сложнее подружиться, чем с выражением, стоящим под знаком логарифма!
Следуя этому правилу, я заменю \( \displaystyle \log_{x}{2}\) на \( \displaystyle \frac{1}{{{\log }_{2}}x}\) и \( \displaystyle {{\log }_{2x}}2\) на \( \displaystyle \frac{1}{\log_{2}{2x}}=\frac{1}{\left( 1+{{\log }_{2}}x \right)}\). Тогда я получу:
\( \displaystyle \frac{2}{{{\log }_{2}}x}+\frac{6}{1+{{\log }_{2}}x}=3\)
Ну а дальнейшие шаги тебе уже знакомы. Заменяй и ищи корни!
В результате ты отыщешь два корня исходного уравнения: \( \displaystyle {{x}_{1}}=4,{{x}_{2}}=\frac{\sqrt[3]{4}}{2}\)
Пришла пора тебе показать, чему ты научился! Постарайся вначале самостоятельно решить следующие (не самые легкие) примеры:
- \( \displaystyle 3{{\log }_{x}}16-4{{\log }_{16}}x=2{{\log }_{2}}x\)
- \( \displaystyle {{\log }_{x}}(5{{x}^{2}})\cdot log\frac{2}{5}x=1\)
- \( \displaystyle {{\log }_{\frac{x}{2}}}{{x}^{2}}-14{{\log }_{16x}}{{x}^{3}}+40{{\log }_{4x}}\sqrt{x}=0\)
- \( \displaystyle 1+{{\log }_{x}}\frac{4-x}{10}=\left( \lg {{x}^{2}}-1 \right){{\log }_{x}}10\)
1. Здесь все достаточно стандартно: я буду стараться свести мое исходное уравнение к такому, чтобы была удобна замена \( \displaystyle t={{\log }_{2}}x\).
Что мне для этого потребуется? Во-первых, преобразовать первое выражение слева (вынести четвертую степень двойки перед логарифмом) и вынести степень двойки из основания второго логарифма. Тогда я получу:
\( \displaystyle 12{{\log }_{x}}2-{{\log }_{2}}x=2{{\log }_{2}}x\)
Осталось всего ничего: «перевернуть» первый логарифм!
2. Здесь я тоже буду стараться «подогнать» мое уравнение под приемлемую замену. Какую же? Пожалуй, мне подойдет \( \displaystyle t={{\log }_{5}}x\).
Так давай не будем терять времени и приступим к преобразованиям!
3. Здесь сразу даже не совсем очевидно, что мы будем заменять. Есть одно золотое правило – не знаешь, что делать – делай то, что можно! Вот им я и воспользуюсь!
\( \displaystyle 2{{\log }_{\frac{x}{2}}}x-14\cdot 3{{\log }_{16x}}x+40\cdot 0,5{{\log }_{4x}}x=0\)
Теперь я «переверну» все логарифмы и применю к первому – формулу логарифма разности, а к двум последним – логарифм суммы:
\( \displaystyle \frac{2}{1-{{\log }_{x}}2}-\frac{42}{1+4{{\log }_{x}}2}+\frac{20}{1+2{{\log }_{x}}2}=0\).
Здесь я также пользовался тем, что \( \displaystyle {{\log }_{x}}x=1\) (при \( \displaystyle x>0,x\ne 1\)) и свойством вынесения степени из логарифма.
Ну вот, теперь нам можно применить подходящую замену:
4. \( \displaystyle 1+{{\log }_{x}}\frac{4-x}{10}=\left( \lg {{x}^{2}}-1 \right){{\log }_{x}}10\)
Этот примерчик позаковырестее, однако, я постараюсь решить его вообще не прибегая к замене переменной!
Давай опять, будем делать, что можно: а можно для начала разложить логарифм слева по формуле для логарифма отношения, а также вынести двойку вперед у логарифма в скобках. В итоге у меня получится:
\( \displaystyle 1+{{\log }_{x}}\left( 4-x \right)-{{\log }_{x}}10=\left( 2lgx-1 \right){{\log }_{x}}10\)
Что будем делать дальше? Непонятно. А что делать можно? Можно перенести \( \displaystyle {{\log }_{x}}10\) вправо и вынести его как общий множитель. Ура! У нас ушла минус единица!
\( \displaystyle 1+{{\log }_{x}}\left( 4-x \right)=2lgx{{\log }_{x}}10\)
Ну а теперь та самая формула, которую мы уже применяли! Так как \( \displaystyle {{\log }_{x}}10=\frac{1}{lgx}\), то сократим правую часть! Теперь там вообще просто стоит двойка! Перенесем к ней слева единицу, окончательно получим:
\( \displaystyle {{\log }_{x}}\left( 4-x \right)=1\)
Как решать такие уравнения, ты уже знаешь. Корень находится без труда, и он равен \( \displaystyle 2\). Напоминаю тебе о проверке!
Ну вот, теперь ты, как я надеюсь, научился решать достаточно сложные задачи, которые « в лоб» не одолеешь! Но логарифмические уравнения бывают еще более коварными! Вот например такие:
\( \displaystyle \log {{~}_{2}}x~+{{\log }_{3}}~x~=1.\)
Здесь уже, увы, предыдущий способ решения не даст ощутимых результатов. Как ты думаешь, почему? Да, никакой «обратности» логарифмов здесь уже не наблюдается. Этот наиболее общий случай, конечно, тоже поддается решению, но мы уже применяем вот такую формулу:
\( \displaystyle {{\log }_{a}}b=\frac{{{\log }_{c}}b}{{{\log }_{c}}a}\)
Уж этой формуле все равно, имеется у вас «противоположность» или нет. Ты можешь спросить, а чему выбирать основание \( \displaystyle c\)? Мой ответ – это не имеет никакого значения. Ответ в итоге не будет зависеть от этого \( \displaystyle c\). Традиционно используют либо натуральный, либо десятичный логарифм. Хотя это и не принципиально. Я, например, буду применять десятичный:
\( \displaystyle \frac{lgx}{\lg 2}+\frac{lgx}{\lg 3}=1\)
\( \displaystyle lgx\left( \lg 2+\lg 3 \right)=\lg 2\lg 3\)
\( \displaystyle lgxlg6=\lg 2\lg 3\)
\( \displaystyle lgx=\frac{\lg 2\lg 3}{\lg 6}\)
Отставлять ответ в таком виде – форменное безобразие! Давайте я вначале запишу по определению, что
\( \displaystyle x={{10}^{\frac{\lg 2\lg 3}{\lg 6}}}={{\left( {{10}^{\lg 2}} \right)}^{\frac{lg3}{\lg 6}}}\)
Теперь пришло время воспользоваться: внутри скобок – основным логарифмическим тождеством, а снаружи (в степени) – превратить отношение в один логарифм: \( \displaystyle {{10}^{\lg 2}}=2,\frac{\lg 3}{\lg 6}={{\log }_{6}}3\), тогда окончательно получим вот такой «странный» ответ: \( \displaystyle x={{2}^{{{\log }_{6}}3}}\).
Дальнейшие упрощения, увы, нам уже недоступны.
Давай сделаем проверку вместе:
\( \displaystyle {{\log }_{2}}{{2}^{{{\log }_{6}}3}}+{{\log }_{3}}{{2}^{{{\log }_{6}}3}}=1\)
\( \displaystyle {{\log }_{6}}3\cdot {{\log }_{2}}2+{{\log }_{6}}3\cdot {{\log }_{3}}2=1\)
\( \displaystyle {{\log }_{6}}3\left( 1+{{\log }_{3}}2 \right)=1\)
\( \displaystyle {{\log }_{6}}3\cdot {{\log }_{3}}6=1\)
\( \displaystyle 1=1\)
Верно! Кстати, еще раз вспомни, из чего следует предпоследнее равенство в цепочке!
\( \displaystyle {{\log }_{3x+7}}~\left( 9+12x+4{{x}^{2}} \right)+{{\log }_{2x+3}}\left( 6{{x}^{2}}~+23x+21 \right)=4.\)
В принципе, решение этого примера тоже можно свести к переходу к логарифму по новому основанию, только тебя должно уже пугать то, что получится в итоге. Давай попробуем поступить разумнее: как можно лучше преобразуем левую часть.
\( \displaystyle 9+12x+4{{x}^{2}}={{\left( 2x+3 \right)}^{2}}\)
\( \displaystyle 6{{x}^{2}}~+23x+21=\left( 3x+7 \right)\left( 2x+3 \right)\)
Кстати, а как по-твоему я получил последнее разложение? Верно, я применил теорему о разложении квадратного трехчлена на множители, а именно:
Если \( \displaystyle {{x}_{1}}\), \( \displaystyle {{x}_{2}}\)– корни уравнения \( \displaystyle a{{x}^{2}}+bx+c=0\), то:
\( \displaystyle a{{x}^{2}}+bx+c=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)\)
Ну вот, теперь я перепишу мое исходное уравнение вот в таком виде:
\( \displaystyle {{\log }_{3x+7}}~{{\left( 2x+3 \right)}^{2}}+{{\log }_{2x+3}}~\left( 3x+7 \right)\left( 2x+3 \right)=4\)
\( \displaystyle 2{{\log }_{3x+7}}~\left( 2x+3 \right)+{{\log }_{2x+3}}~\left( 3x+7 \right)=3\)
А вот решить такую задачу нам уже вполне по силам!
Так как \( \displaystyle {{\log }_{2x+3}}~\left( 3x+7 \right)=1/{{\log }_{3x+7}}~\left( 2x+3 \right)\), то введем замену \( \displaystyle t={{\log }_{3x+7}}~\left( 2x+3 \right)\).
Тогда мое исходное уравнение примет вот такой простой вид: \( \displaystyle \frac{2}{t}+t-3=0\)
Его корни равны: \( \displaystyle {{t}_{1}}=2,{{t}_{2}}=1\), тогда
\( \displaystyle {{\log }_{3x+7}}~\left( 2x+3 \right)=1\), откуда \( \displaystyle 3x+7=2x+3,{{x}_{1}}=-4\)
\( \displaystyle {{\log }_{3x+7}}~\left( 2x+3 \right)=2\), откуда \( \displaystyle {{\left( 3x+7 \right)}^{2}}=\left( 2x+3 \right)\) – данное уравнение корней не имеет.
Тебе осталось сделать проверку!
Следующее уравнение попробуй решить самостоятельно. Не торопись и будь внимателен, тогда удача будет на твоей стороне!
\( \displaystyle {{\log }_{5}}\left( 5+3x \right)={{\log }_{5}}3\cdot {{\log }_{3}}\left( 2x+10 \right)\)
Готов? Давай посмотрим, что у нас получилось.
На самом деле, пример решается в два действия:
1. Преобразуем \( \displaystyle {{\log }_{5}}3=\frac{1}{{{\log }_{3}}5}\)
2. Теперь справа у меня стоит выражение \( \displaystyle \frac{{{\log }_{3}}\left( 2x+10 \right)}{{{\log }_{3}}5}\), которое равно \( \displaystyle {{\log }_{5}}\left( 2x+10 \right)\)
Таким образом, исходное уравнение свелось к простейшему:
\( \displaystyle {{\log }_{5}}~\left( 5+3x \right)={{\log }_{5}}\left( 2x+10 \right)\)
\( \displaystyle x=5\).
Проверка говорит о том, что данное число в самом деле является корнем уравнения.
Метод логарифмирования (для решения смешанных уравнений)
Ну и напоследок я очень кратко остановлюсь на методах решения некоторых смешанных уравнений. Само собой, я не берусь охватить все смешанные уравнения, а покажу приемы решения самых простых.
Например,
\( \displaystyle {{x}^{{{\log }_{3}}x}}=3\)
Такое уравнение может быть решено методом логарифмирования. Все, что тебе нужно сделать, это взять логарифм от обеих частей. Ясно, что поскольку у нас уже есть логарифм по основанию \( \displaystyle 3\), то логарифмировать я буду по тому же основанию:
\( \displaystyle {{\log }_{3}}({{x}^{{{\log }_{3}}x}})={{\log }_{3}}3=1\)
Теперь я вынесу степень из выражения слева:
\( \displaystyle {{\log }_{3}}x\cdot {{\log }_{3}}x=1\)
И разложу выражение на множители по формуле разности квадратов:
\( \displaystyle ({{\log }_{3}}x-1)({{\log }_{3}}x+1)=0\)
\( \displaystyle {{x}_{1}}=3,{{x}_{2}}=\frac{1}{3}\)
Проверка как всегда на твоей совести.
Последний пример данной статьи попробуй решить самостоятельно!
\( \displaystyle {{x}^{2{{\lg }^{2}}x}}=0.1{{x}^{3}}\)
Проверяем: берем логарифм по основанию \( \displaystyle 10\) от обеих частей уравнения:
\( \displaystyle \lg ({{x}^{2{{\lg }^{2}}x}})=\lg 0.1{{x}^{3}}\)
Выношу степень слева и раскалываю по формуле суммы справа:
\( \displaystyle 2{{\lg }^{2}}x\cdot \lg x=\lg 0.1+\lg {{x}^{3}}\)
\( \displaystyle 2{{\lg }^{3}}x=-1+3lgx\)
\( \displaystyle 2{{\lg }^{3}}x-3lgx+1=0\)
Замена \( \displaystyle t=lgx\)
\( \displaystyle 2{{t}^{3}}-3t+1=0\)
Угадываем один из корней: \( \displaystyle {{t}_{1}}=1\) является корнем. В статье, посвященной решению показательных уравнений, я рассказывал о том, как делить один многочлен «уголком» на другой. Здесь нам понадобится поделить \( \displaystyle 2{{t}^{3}}-3t+1\) на \( \displaystyle t-1\). В итоге мы получим:
\( \displaystyle 2{{t}^{3}}-3t+1=\left( t-1 \right)\left( 2{{t}^{2}}+2t-1 \right)\)
\( \displaystyle 2{{t}^{2}}+2t-1=0\)
\( \displaystyle {{\text{t}}_{2}}=\frac{\sqrt{3}-1}{2},{{t}_{3}}=\frac{-1-\sqrt{3}}{2}\)
Тогда \( \displaystyle {{x}_{1}}=10\), \( \displaystyle {{x}_{2}}={{10}^{\frac{\sqrt{3}-1}{2}}}\), \( \displaystyle {{x}_{3}}={{10}^{\frac{-1-\sqrt{3}}{2}}}\).
Проверку проведи, по-возможности, сам (хотя в данном случае, особенно с последними двумя корнями, она будет непростой).
Мини-максный метод решения смешанных уравнений (для суперпродвинутых)
В дополнение к уже изложенному материалу, я предлагаю нам с тобой рассмотреть еще один способ решения смешанных уравнений, содержащих логарифмы.
Однако здесь я буду рассматривать такие уравнения, которые не могут быть решены рассмотренным ранее методом логарифмирования обеих частей. Данный способ имеет название мини-максного.
Данный метод применим не только при решении смешанных уравнений, но также оказывается полезным при решении некоторых неравенств.
Итак, вначале введем следующие основные определения, которые необходимы для применения мини-максного метода.
Определение 1:
\( \displaystyle f(x)\) монотонно возрастает на\( \displaystyle [a,b]\), если для любых \( \displaystyle {{x}_{1}},{{x}_{2}}\) из этого промежутка из того, что \( \displaystyle {{x}_{1}}<{{x}_{2}}\) следует, что \( \displaystyle f\left( {{x}_{1}} \right)<f({{x}_{2}})\) и наоборот, из того, что \( \displaystyle {{x}_{1}}>{{x}_{2}}\) следует, что \( \displaystyle f({{x}_{1}})>f({{x}_{2}}).\)
Определение 2:
\( \displaystyle f(x)\) монотонно убывает на\( \displaystyle [a,b]\), если для любых \( \displaystyle {{x}_{1}},~{{x}_{2}}\) из этого промежутка из того, что \( \displaystyle {{x}_{1}}<{{x}_{2}}\) следует, что \( \displaystyle f\left( {{x}_{1}} \right)>f({{x}_{2}})\) и наоборот, из того, что \( \displaystyle {{x}_{1}}>{{x}_{2}}\) следует, что \( \displaystyle f\left( {{x}_{1}} \right)<f({{x}_{2}}).\)
Простые рисунки иллюстрируют эти определения:
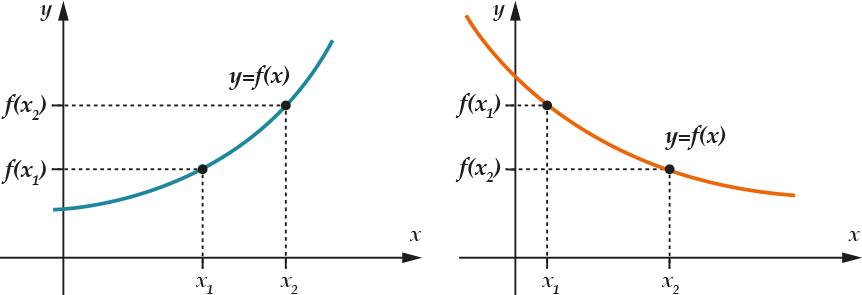
Функция на рисунке слева – монотонно возрастающая, а справа – монотонно убывающая. Теперь обратимся к логарифмической функции \( \displaystyle f(x)=lo{{g}_{a}}x\), известно, что выполняется следующая:
Теорема. Если \( \displaystyle a>1\), то функция \( \displaystyle f(x)=lo{{g}_{a}}x\) является монотонно возрастающей, если \( \displaystyle 0<a<1\), то функция\( \displaystyle f(x)=lo{{g}_{a}}x\) является монотонно убывающей.
На рисунке приведены примеры монотонно возрастающей и монотонно убывающей логарифмической функции.
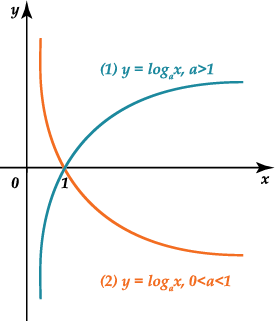
Опишем непосредственно сам мини-максный метод
Я думаю, что ты понимаешь, от каких слов произошло такое название? Верно, от слов минимум и максимум. Кратко метод можно представить в виде:
\( \displaystyle \left\{ \begin{array}{l}f\left( x \right)=g\left( x \right)\\f\left( x \right)\ge A\\g\left( x \right)\le A\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}f\left( x \right)=A\\g\left( x \right)=A\end{array} \right.\)
Наша самая главная цель – это найти вот эту самую константу \( \displaystyle A\), чтобы далее свести уравнение к двум более простым. Для этого могут быть полезны свойства монотонности логарифмической функции, сформулированные выше.
Теперь давай рассмотрим конкретные примеры:
- \( \displaystyle {{\log }_{\frac{1}{3}}}\left( 1+{{\left( {{x}^{2}}-3x+2 \right)}^{2}} \right)=\sqrt{{{x}^{2}}-6x+8}\)
- \( \displaystyle {{\left( 4{{x}^{2}}-7{x} -2 \right)}^{2}}+\log _{5}^{5}\left( 2{{x}^{2}}-11x+15 \right)=0\)
- \( \displaystyle {{\log }_{3}}\left( {{x}^{2}}+6x+18 \right)=2{{\sin }^{2}}\frac{\pi x}{6}\)
1. Вначале рассмотрим левую часть. Там стоит логарифм с основанием меньше \( \displaystyle 0<a<1\).
По теореме, сформулированной выше, какой оказывается функция \( \displaystyle y={{\log }_{a}}t\)? Она убывает. При этом, \( \displaystyle t=1+{{\left( {{x}^{2}}-3x+2 \right)}^{2}}\ge 1\), а значит, \( \displaystyle {{\log }_{a}}t\le 0\).
С другой стороны, по определению корня:
\( \displaystyle \sqrt{{{x}^{2}}-6x+8}\ge 0\).
Таким образом, константа \( \displaystyle A\) найдена и равна \( \displaystyle 0\). Тогда исходное уравнение равносильно системе:
\( \displaystyle \left\{ \begin{array}{l}\sqrt{{{x}^{2}}-6x+8}=0\\{{\log }_{\frac{1}{3}}}\left( 1+{{\left( {{x}^{2}}-3x+2 \right)}^{2}} \right)=0\end{array} \right.\)
Первое уравнение имеет корни \( \displaystyle {{x}_{1}}=4,{{x}_{2}}=2\), а второе: \( \displaystyle {{x}_{1}}=1,{{x}_{2}}=2\).
Таким образом, общий корень равен \( \displaystyle 2\), и данный корень будет корнем исходного уравнения. На всякий случай сделай проверку, чтобы убедиться в этом.
Ответ: \( \displaystyle 2\)
2. \( \displaystyle {{\left( 4{{x}^{2}}-7{x} -2 \right)}^{2}}+\log _{5}^{2}\left( 2{{x}^{2}}-11x+15 \right)=0\)
Давай сразу задумаемся, что здесь написано? Я имею в виду общую структуру. Здесь сказано, что сумма двух квадратов равна нулю. Когда это возможно? Только тогда, когда оба этих числа по отдельности равны нулю. Тогда перейдем к следующей системе:
\( \displaystyle \left\{ \begin{array}{l}{{\left( 4{{x}^{2}}-7{x} -2 \right)}^{2}}=0\\\log _{5}^{2}\left( 2{{x}^{2}}-11x+15 \right)=0\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}{{x}_{1}}=2;\\{{x}_{2}}=-0,25\end{array} \right.\\\left[ \begin{array}{l}{{x}_{1}}=3;\\{{x}_{2}}=2,5\end{array} \right.\end{array} \right.\)
Общих корней у первого и второго уравнений нет, тогда и исходное уравнение корней не имеет.
Ответ: нет решений.
3. \( \displaystyle {{\log }_{3}}\left( {{x}^{2}}+6x+18 \right)=2{{\sin }^{2}}\frac{\pi x}{6}\)
Давай вначале рассмотрим правую часть – она попроще. По определению синуса:
\( \displaystyle -1\le sint\le 1\), откуда \( \displaystyle 0\le {{\sin }^{2}}t\le 1\), и тогда \( \displaystyle 0\le 2{{\sin }^{2}}t\le 2.\) Поэтому \( \displaystyle 0\le 2{{\sin }^{2}}\frac{\pi x}{6}\le 2.\)
Теперь вернемся к левой части: рассмотрим выражение, стоящее под знаком логарифма:
\( \displaystyle {{x}^{2}}+6x+18\)
Попытка найти корни у уравнения \( \displaystyle {{x}^{2}}+6x+18=0\) не приведет к положительному результату. Но тем не менее, мне надо как-то это выражение оценить. Ты, конечно, знаешь такой метод, как выделение полного квадрата. Его я здесь и применю.
\( \displaystyle {{x}^{2}}+6x+18={{x}^{2}}+2\cdot 3\cdot x+9+9={{\left( x+3 \right)}^{2}}+9\ge 9\)
Тогда \( \displaystyle {{\log }_{3}}\left( {{x}^{2}}+6x+18 \right)={{\log }_{3}}\left( {{\left( x+3 \right)}^{2}}+9 \right)\)
Так как \( \displaystyle y={{\log }_{3}}t\) – функция возрастающая, то из \( \displaystyle {{\left( x+3 \right)}^{2}}+9\ge 9\) cледует, что \( \displaystyle {{\log }_{3}}\left( {{\left( x+3 \right)}^{2}}+9 \right)\ge {{\log }_{3}}9=2\).
Таким образом, \( \displaystyle {{\log }_{3}}\left( {{\left( x+3 \right)}^{2}}+9 \right)\ge 2\)
Тогда наше исходное уравнение равносильно следующей системе:
\( \displaystyle \left\{ \begin{array}{l}{{\log }_{3}}\left( {{x}^{2}}+6x+18 \right)=2\\2{{\sin }^{2}}\frac{\pi x}{6}=2\end{array} \right.\)
Я не знаю, знаком ты или нет с решением тригонометрических уравнений, поэтому я сделаю так: решу первое уравнение (оно имеет максимум два корня), а потом результат подставлю во второе:
\( \displaystyle {{\log }_{3}}\left( {{x}^{2}}+6x+18 \right)=2\)
\( \displaystyle {{x}_{1}}=-3\) (можешь сделать проверку и убедиться, что это число является корнем первого уравнения системы)
Теперь я подставлю его во второе уравнение:
\( \displaystyle 2{{\sin }^{2}}\frac{\pi x}{6}=2\)
\( \displaystyle 2{{\sin }^{2}}\frac{\pi \left( -3 \right)}{6}=2\)
\( \displaystyle {{\sin }^{2}}\frac{-\pi }{2}=1\)
\( \displaystyle 1=1.\)
Ответ: \( \displaystyle x=-3\)
Ну как, теперь тебе стала ясна техника применения мини-максного метода? Тогда постарайся решить следующий пример самостоятельно.
\( \displaystyle 1+\left| {{\log }_{4}}\left( 9{{x}^{2}}-39x+43 \right) \right|=\left| \cos \cos \left( {x} -2 \right)\cos \left( x \right) \right|\)
Готов? Давай проверим:
Левая часть – сумма двух неотрицательных величин (единицы и модуля) а потому, левая часть не меньше единицы, причем она равна единице только тогда, когда
\( \displaystyle \left| {{\log }_{4}}\left( 9{{x}^{2}}-39x+43 \right) \right|=0\)
В то же время правая часть – это модуль (значит, больше нуля) произведения двух косинусов (значит не более единицы), тогда:
\( \displaystyle \left| {{\log }_{4}}\left( 9{{x}^{2}}-39x+43 \right) \right|=0\)
Тогда исходное уравнение равносильно системе:
\( \displaystyle \left\{ \begin{array}{l}1+|{{\log }_{4}}\left( 9{{x}^{2}}-39x+43 \right)|=1\\\left| \cos \cos \left( {x} -2 \right)\cos \left( x \right) \right|=1\end{array} \right.\)
Я опять предлагаю решить первое уравнение и результат подставить во второе:
\( \displaystyle 1+|{{\log }_{4}}\left( 9{{x}^{2}}-39x+43 \right)|=1\)
\( \displaystyle |{{\log }_{4}}\left( 9{{x}^{2}}-39x+43 \right)|=0\)
\( \displaystyle {{\log }_{4}}\left( 9{{x}^{2}}-39x+43 \right)=0\).
Данное уравнение корней не имеет.
Тогда исходное уравнение также не имеет корней.
Ответ: решений нет.
Бонус: Подборка из 6 вебинаров по решению задачи ЕГЭ №13
И если ты воспринимаешь информацию визуально, посмотри подборку из 6 вебинаров по решению задачи ЕГЭ №13 — там также попадаются логарифмические уравнения и даже смешанные.
Вот в качестве примера один из них:
Очень сложная смешанная задача (тригонометрическая, показательная, логарифмическая)
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Если под корнем сумма числа и корня (a+b^0,5)^0,5 и разность квадратов является полным квадратом, то можно разложить на сумму двух корней по формуле Эйлера. а^2 —b = n. [(a + n)/2]^0,5 + [(a — n)/2]^0,5. В примере будет 25 —24 = 1 =1^2. Следовательно, выражение под корнем можно превратить в квадрат суммы (разности). Получим по формуле Эйлера.
[(5 + 1)/2]^0,5 + [(5 — 1)/2]^0,5 = 3^0,5 + 2^0,5 и то же, но с минусом. У Вас всё верно, но мне не понравился логарифм с экзотическим основанием. Достаточно десятичных. Получим sinx = плюс, минус lg3 : lg[3^0,5 +2^0,5].
x =(73,43; —73,43; 106,57; —106,57) градусов. Первый ответ надо отбросить.
Здраствуйте, во втором примере мини-максного метода логарифм по основанию 5 равняется нулю, не значит ли, что аргумент необходимо приравнивать к 1, а не 0?
Здравствуйте, хороший материал, но есть и такие уравнения 8=5lg(6*100/x)
Спасибо большое за Вашу работу.
Спасибо, Нина! Очень приятно слышать!
Спасибо Вам и низкий поклон за грамотную и, что немаловажно, в доступной форме подачу относительно сложного материала. Приятно встречать на просторах интернета умных людей!
Василий, спасибо огромное за теплые слова. Очень приятно слышать.
Некоторые комментарии прошлых лет к этой статье:
Ольга
04 апреля 2018
Спасибо, очень понравилось объяснение. Опечатка только в первом примере, вместо корня результат проверки в ответе указан.
Александр (админ)
04 апреля 2018
Спасибо за наблюдательность, Ольга! Да, действительно, опечатка. Поправили.
Александр (админ)
04 апреля 2018
И за теплые слова тоже спасибо! )
Антон
11 апреля 2018
Спасибо огромное, вы меня прям спасли!
Александр (админ)
11 апреля 2018
Скорая помощь на марше! 🙂 Пожалуйста, Антон. Мы рады, что тебе понравилось. Оказывается математика может быть простой, правда? )
;))))
17 апреля 2018
да
Люба
01 мая 2018
Спасибо огромное, за очень простое и понятное объяснение
Александр (админ)
01 мая 2018
Пожалуйста, Люба. Держи в курсе как пройдет экзамен. Можно прямо здесь написать помог тебе наш сайт или нет к нему подготовиться )
Сергей
07 мая 2018
Спасибо вашему сайту. Добавил в закладки. По поводу 7-го примера для самостоятельного решения. Мне кажется, вы забыли дописать квадрат над «х»
Александр (админ)
12 мая 2018
Спасибо, Сергей за внимательность! Проверим обязательно.
Александр
12 мая 2018
в объяснении 5 примера есть опечатка, там стоит 3 — х, а должно быть 7 — х. А так спасибо вам)
Александр (админ)
12 мая 2018
И вам спасибо, Александр! Опечатку устраним. Будем рады, если вы найдете еще. ))
Кирилл
09 января 2019
Александр, спасибо большое за хорошее, подробное и понятное объяснение! Очень приятно осознавать, что есть такие доброжелательные люди)
Александр (админ)
09 января 2019
Пожалуйста, Кирилл. Очень приятно слышать. За объяснение надо благодарить нашего репетитора Алексея Шевчука. Это он их писал. Но я ему передам. )
Марина Варновская
23 января 2019
Большое спасибо! Все очень толково. Хотелось бы еще скачать материал.
Александр (админ)
23 января 2019
Спасибо, Марина. По поводу возможности скачивания — пока не получается. Сейчас весь учебник сделан так, что скачать текст и скопировать невозможно. Нужно либо делать сканы всего текста и выкладывать их на скачивание, либо делать текст и отдельные картинки. И то и другое — большие трудозатраты и деньги. Пока мы этого сделать не можем. Но мы думаем над этим.
Рашид
25 января 2019
Спасибо вам большое за этот проект!) Все очень понятно и доходчиво изложено, а то что все изученное можно закрепить примерами, так это вообще отдельный плюс) Обязательно куплю полную версию и посоветую друзьям 🙂
Александр (админ)
25 января 2019
И тебе спасибо, Рашид. Очень рады, что понравилось!
Виктор
27 января 2019
Спасибо большое за столь подробный разбор примеров. Но ни в одном не нашел случая, чтобы решить данное уравнение: log7log4(x-2)=0, с виду оно кажется в миллион раз проще, чем те, которые я уже решал. Но с ним у меня есть некие трудности. Не могли бы Вы мне, как решаются такие примеры? Как довести его до обычного простого уравнения, где нужно только убрать логарифмы и решить. Заранее спасибо!
Алексей Шевчук
04 февраля 2019
Виктор, сделай замену log4(x-2) = y, тогда задача сведётся к двум простым логарифмическим уравнениям.
Даагмар
31 января 2019
Спасибо за невероятно ясные и точные пояснения каждого примера, формулы или уравнения и разжевывания всего этого до уровня ,когда может понять любой. Помогло прояснить многие моменты
Александр (админ)
31 января 2019
И тебе спасибо, Даагмар!
Алия
13 февраля 2019
Здравствуйте. Мне непонятен один момент во втором уравнении метода Мини-максный. Почему больше или равно 9, а не нулю?
Алексей Шевчук
13 февраля 2019
Алия, там больше или равно 9, потому что первая скобка в квадрате, и она точно не отрицательна. Потом мы сравниваем логарифм от этого выражения с логарифмом от 9.
Галина
27 июля 2019
Спасибо, за статью.
Александр (админ)
28 июля 2019
Пожалуйста, Галина! Рады, что понравилось!
Океан
30 октября 2019
Спасибо вам, уже пару раз пользуюсь вашим сайтом, он просто превосходный, помогает на контрольный работах. Спасибо вам большое
Александр (админ)
30 октября 2019
Рад слышать, Океан, что сайт помогает на контрольных. Желаю вам подготовиться с помощью наших сайтов youclever.org и 100gia.ru ко всем экзаменам! 🙂
Star
09 апреля 2020
Спасибо Вам огромное!!!
Александр (админ)
09 апреля 2020
Пожалуйста, Star, заходите еще и удачи на экзаменах!
admin
28 апреля 2020
spasibckii
Александр (админ)
28 апреля 2020
Пожалуйста 🙂
Виталий Торопов
24 мая 2020
Проверку делать не обязательно, можно воспользоваться ОДЗ.
Алексей Шевчук
05 июня 2020
Виталий, конечно. Либо проверка, либо ОДЗ.
Асад
24 июня 2020
Спасибо большое, очень понятно и внятно объяснили. Лучше чем многие видео на ютубе.
Александр (админ)
24 июня 2020
Спасибо, Асад! Очень приятно слышать такое сравнение )