Что такое функция
Понятие «функция» пронизывает все сферы математики и не только.
Мы все знаем, что функция записывается как \( \displaystyle y=f\left( x \right)\), но можешь ли ты ответить, что обозначает эта формула?
Если да, то ты большой молодец!
А если нет, – не страшно! Сейчас быстренько во всем разберемся!
Функции — коротко о главном
Определение функции:
Функцией называется правило \( \displaystyle f\), по которому каждому элементу \( \displaystyle x\) множества \( \displaystyle X\) ставится в соответствие единственный элемент \( \displaystyle y\) множества \( \displaystyle Y\).
- \( \displaystyle y=f\left( x \right)\) – это формула, обозначающая функцию, то есть зависимость одной переменной от другой;
- \( \displaystyle x\) – переменная величина, или, аргумент;
- \( \displaystyle y\) – зависимая величина – изменяется при изменении аргумента, то есть согласно какой-либо определенной формуле \( \displaystyle f\), отражающей зависимость одной величины от другой.
Свойства и способы задания:
Допустимые значения аргумента, или область определения функции \( \displaystyle D\left( y \right)\) – это то, что связано с возможными \( \displaystyle x\), при которых функция имеет смысл.
Область значений функции \( \displaystyle E\left( y \right)\) – это то, какие значения принимает \( \displaystyle y\), при допустимых значениях \( \displaystyle x\).
Существует 4 способа задания функции:
- аналитический (с помощью формул);
- табличный;
- графический;
- словесное описание.
Основные виды функций:
- линейная функция: \( \displaystyle y=kx+b\), где \( \displaystyle k\), \( \displaystyle b\) – действительные числа;
- квадратичная функция: \( \displaystyle y=a{{x}^{2}}+bx+c\), где \( \displaystyle a\ne 0\);
- обратная пропорциональность: \( \displaystyle y=\frac{k}{x}\), где \( \displaystyle k\ne 0\).
Сейчас все это разберем подробнее.
Что такое функция — человеческим языком
Так вот, функция отражает зависимость величин друг от друга: то есть при изменении одного числа \( \displaystyle x\), по некоторому закону \( \displaystyle f\left( x \right)\) изменяется \( \displaystyle y\).
Зависимость, или взаимосвязь – вот ключевые слова при определении понятия функции.
Попробуй самостоятельно придумать несколько примеров из жизни, где четко проявляется зависимость одного от другого.
И?… Не можешь придумать ни один пример? Как так! Смотри:
Допустим автомобиль движется со средней скоростью \( \displaystyle 110\) км/ч, как тогда выразить зависимость пути \( \displaystyle S\) от времени \( \displaystyle t\)?
Правильно:
\( \displaystyle S=110\cdot t\)
То есть чем больше времени автомобилист проведет за рулем, тем больше расстояние он преодолеет на своем автомобиле. Чем не зависимость?
Что в этом случае будет \( \displaystyle y\), что \( \displaystyle x\), и как будет выражено в итоге \( \displaystyle f\left( x \right)\)?
Проведем параллели между физической формулой и привычной нам записью функции \( \displaystyle y=f\left( x \right)\):
- \( \displaystyle y=S\), то есть путь, который проедет автомобилист;
- \( \displaystyle x=t\), время, которое он проведет в пути;
- \( \displaystyle f\left( x \right)=110\cdot x\) зависимость пути от времени, учитывая, что скорость на всем пути постоянна.
Разобрался что к чему? Теперь перейдем на математический язык.
Что такое функция — на языке математики
Итак. Еще раз смотрим на нашу формулу:
\( \displaystyle y=f\left( x \right)\)
Слева стоит \( \displaystyle y\) – это и есть функция. За этой буквой может быть все что угодно: температура, скорость, сила, путь – неважно! \( \displaystyle y\) – зависимая величина.
Она может зависеть от множества критериев. Например, как в нашем случае, зависимость пути от времени, проведенном в дороге при движении с постоянной скоростью.
Справа у нас стоит \( \displaystyle x\). Эта величина переменная, или, как говорят математики, «аргумент».
Логично, что чем больше времени проведет автомобилист в дороге, тем большее расстояние он проедет (конечно, если скорость будет постоянна, и он не встрянет намертво в пробках).
Справа у нас также есть \( \displaystyle f\), за этим скрываются все действия, совершаемые над \( \displaystyle x\).
В нашем случае мы говорим, что \( \displaystyle S=\nu \cdot t\), а так как \( \displaystyle \nu =110\)км/ч, то под \( \displaystyle f\) скрывается умножение на \( \displaystyle 110\), вот мы и получаем – \( \displaystyle f\left( x \right)=110\cdot x\).
Теперь, думаю, тебе все понятно?
Подведем итог:
- \( \displaystyle y=f\left( x \right)\) – это формула, обозначающая функцию, то есть зависимость одной переменной от другой;
- \( \displaystyle x\) – переменная величина, или, аргумент;
- \( \displaystyle y\) – зависимая величина – изменяется при изменении аргумента, то есть \( \displaystyle x\) согласно какой-либо определенной формуле \( \displaystyle f\), отражающей зависимость одной величины от другой.
Теперь, когда ты понял суть понятия «функция» и знаешь, что такое переменная величина, а что постоянная, посмотрим на определение функции, каким его дают математики.
Определение функции
Функцией называется правило \( \displaystyle f\), по которому каждому элементу \( \displaystyle x\) множества \( \displaystyle X\) ставится в соответствие единственный элемент \( \displaystyle y\) множества \( \displaystyle Y\).
Вроде и \( \displaystyle x\) есть… и \( \displaystyle y\) есть, и даже правило \( \displaystyle f\) есть, но что это за множества такие?
«О них мы ни слова не говорили!» – воскликнешь ты. Не паникуй! 🙂 Множества – это очень просто, сейчас все-все проясним!
Область определения функции
Вернемся к нашему примеру.
Автомобилист едет с постоянной скоростью и проезжает расстояние, которое зависит от того, сколько времени он провел в пути. Все верно?
Разбираемся дальше. Мы говорили, что \( \displaystyle x=t\), это как раз и есть время, проведенное в пути.
Каким оно может быть? Ты сейчас можешь быть крайней удивлен такой постановкой вопроса, но все же, каким может быть это время?
Правильно, чисто теоретически от \( \displaystyle 0\) до \( \displaystyle +\infty \).
Вот ты сам и определил для нашего конкретного случая множество \( \displaystyle X\), а иначе говоря, допустимые значения аргумента или область определения функции \( \displaystyle D\left( y \right)\).
Запомнить очень легко: что определяет нашу функцию? От чего зависит игрек, и что мы меняем?
Функцию определяет икс! Соответственно, область определения – это возможные значения \( \displaystyle x\).
Теперь давай рассматривать, что такое множество \( \displaystyle Y\).
Область значений функции
Думаю, ты сам ответишь, что путь не может быть отрицательным, так что \( \displaystyle y=S\) в нашей с тобой придуманной функции так же может принимать значения в промежутке от \( \displaystyle 0\) до \( \displaystyle +\infty \).
Это называется областью значений функции \( \displaystyle E\left( y \right)\), то есть множество \( \displaystyle Y\), которые существуют для данной функции.
Итак, сделаем небольшой вывод по последнему:
Допустимые значения аргумента, или область определения функции \( \displaystyle D\left( y \right)\) – это то, что связано с возможными \( \displaystyle x\), при которых функция имеет смысл.
Область значений функции \( \displaystyle E\left( y \right)\) – это то, какие значения принимает \( \displaystyle y\), при допустимых значениях \( \displaystyle x\).
Легко? То-то же.
Давай потренируемся находить области определения функции и ее допустимые значения.
Область определения функции по графикам

Решение
Обязательно пробуй сначала решать самостоятельно!
- (А) \( \displaystyle D\left( y \right)=\left( -\infty ;+\infty \right)\);
- (Б) \( \displaystyle D\left( y \right)=\left( -2;2 \right)\cup \left( 2;6 \right)\);
- (В) \( \displaystyle D\left( y \right)=\left[ 0;+\infty \right)\);
- (Г) \( \displaystyle D\left( y \right)=\left( -\infty ;+\infty \right)\).
Все верно? Молодец! Что-то не понятно? Спрашивай в комментариях!
Теперь попробуем найти область значения фунции.
Области значений функции по графикам
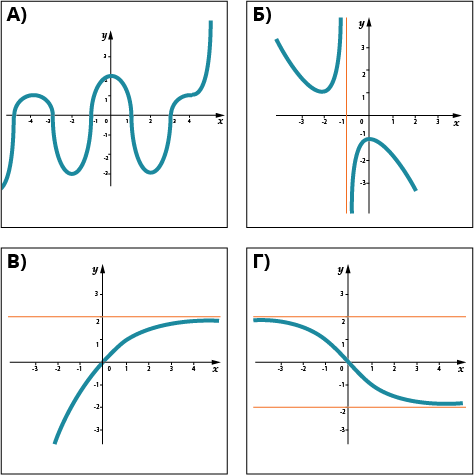
Решение:
- (А) \( \displaystyle E\left( y \right)=\left( -\infty ;+\infty \right)\);
- (Б) \( \displaystyle E\left( y \right)=\left( -\infty ;-1 \right]\cup \left[ 1;+\infty \right)\);
- (В) \( \displaystyle E\left( y \right)=\left( -\infty ;2 \right)\);
- (Г) \( \displaystyle E\left( y \right)=\left( -2;2 \right)\).
Сошлось? Молодец!
Еще раз поработаем с графиками, только теперь чуть-чуть посложнее…
Области значений и определения функции по графикам
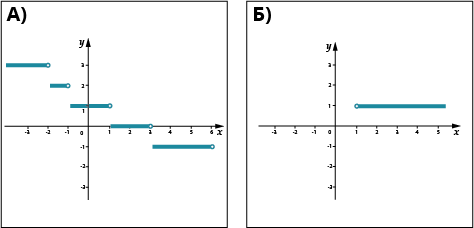
Решение:
(А) \( \displaystyle D\left( y \right)=\left( -\infty;6 \right]\)
\( \displaystyle E\left( y \right)=\left\{ -1 \right\}\cup \left\{ 0 \right\}\cup \left\{ 1 \right\}\cup \left\{ 2 \right\}\cup \left\{ 3 \right\}\);
(Б) \( \displaystyle D\left( y \right)=\left( 1;+\infty \right)\)
\( \displaystyle E\left( y \right)=\left\{ 1 \right\}\).
Область определения функции по формулам (аналитически)
С графиками, я думаю, ты разобрался. Теперь попробуем в соответствии с формулами найти область определения функции (если ты не знаешь, как это сделать, прочитай раздел про ОДЗ — область допустимых значений).
- \( \displaystyle y=\sqrt{x+2}\);
- \( \displaystyle y=\frac{1}{\sqrt{x}}\);
- \( \displaystyle y=\sqrt{{{x}^{2}}+1}\);
- \( \displaystyle y=\frac{1}{x+6}\).
Справился? Смотри ответы:
- \( \displaystyle x\ge -2\), так как подкоренное выражение \( \displaystyle x+2\) должно быть больше или равно нулю;
- \( \displaystyle x>0\), так как на ноль делить нельзя и подкоренное выражение не может быть отрицательным;
- \( \displaystyle x\in \mathbb{R}\), так как \( \displaystyle {{x}^{2}}\ge 0\), соответственно \( \displaystyle {{x}^{2}}+1>0\) при всех \( \displaystyle x\);
- \( \displaystyle x\ne -6\), так как на ноль делить нельзя.
Еще один важный момент
Еще раз повторю определение и сделаю на нем акцент:
Функцией называется правило \( \displaystyle f\), по которому каждому элементу \( \displaystyle x\) множества \( \displaystyle X\) ставится в соответствие единственный элемент \( \displaystyle y\) множества \( \displaystyle Y\).
Заметил? Слово «единственный» – это очень-очень важный элемент нашего определения. Постараюсь объяснить тебе на пальцах.
Допустим, у нас есть функция, заданная прямой. \( \displaystyle y=5x+3\). При \( \displaystyle x=0\), мы подставляем данное значение в наше «правило» и получаем, что \( \displaystyle y=3\).
Одному значению \( \displaystyle x\) соответствует одно значение \( \displaystyle y\). Мы даже можем составить таблицу различных значений и построить график данной функции, чтобы убедится в этом.
| \( \displaystyle x\) | \( \displaystyle 0\) | \( \displaystyle 1\) | \( \displaystyle -1\) | \( \displaystyle 2\) | \( \displaystyle -2\) |
| \( \displaystyle y\) | \( \displaystyle 3\) | \( \displaystyle 8\) | \( \displaystyle -2\) | \( \displaystyle 13\) | \( \displaystyle -7\) |
А вот и график с нашими отмеченными точками:
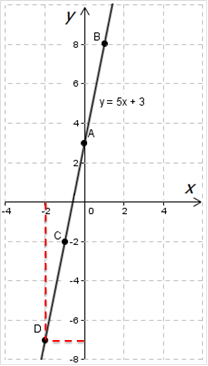
Как ты убедился – графиком является прямая, в которой одному значению \( \displaystyle x\) соответствует одно значение \( \displaystyle y\) (данный факт показан красными линиями).
Соответственно, данная зависимость подходит под определение функции.
А что ты скажешь о такой зависимости: \( \displaystyle y=2{{x}^{2}}-4{x}-1\), то есть параболы? Является ли она функцией? Давай составим также табличку значений:
| \( \displaystyle x\) | \( \displaystyle 0\) | \( \displaystyle 1\) | \( \displaystyle -1\) | \( \displaystyle 2\) | \( \displaystyle -2\) |
| \( \displaystyle y\) | \( \displaystyle -1\) | \( \displaystyle -3\) | \( \displaystyle 5\) | \( \displaystyle -1\) | \( \displaystyle 15\) |
«Смотри! – скажешь ты, – « \( \displaystyle -\mathbf{1}\)» встречается два раза!» Так быть может парабола не является функцией? Нет, является!
То, что «\( \displaystyle -1\)» встречается два раза далеко не повод обвинять параболу в неоднозначности!
Дело в том, что, при расчёте для \( \displaystyle x=0\), мы получили один игрек. И при расчёте с \( \displaystyle x=2\) мы получили один игрек. Так что все верно, парабола является функцией.
Посмотри на график:
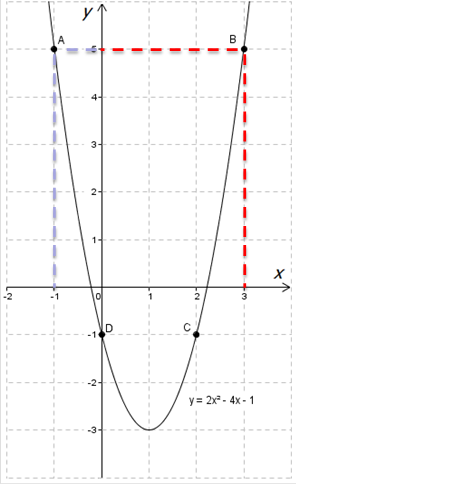
Разобрался? Если нет, вот тебе жизненный пример сооовсем далекий от математики!
Допустим, у нас есть группа абитуриентов, познакомившихся при подаче документов, каждый из которых в разговоре рассказал, где он живет:
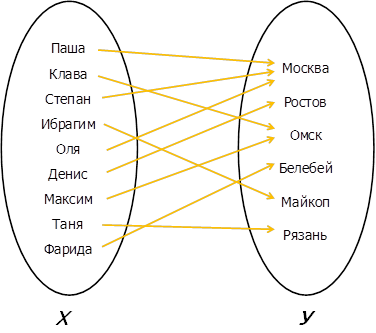
Согласись, вполне реально, что несколько ребят живут в одном городе, но невозможно, чтобы один человек жил в нескольких городах одновременно. Это как бы логичное представление нашей «параболы» – нескольким разным икс соответствует один и тот же игрек.
Теперь придумаем пример, когда зависимость не будет функцией. Допустим, эти же ребята рассказывали, на какие специальности они подали документы:
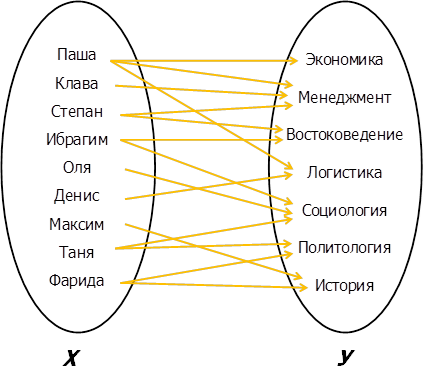
Здесь у нас совершенно другая ситуация: один человек может спокойно подать документы как на одно, так и на несколько направлений. То есть одному элементу \( \displaystyle x\) множества \( \displaystyle X\) ставится в соответствие несколько элементов \( \displaystyle y\) множества \( \displaystyle Y\). Соответственно, это не функция.
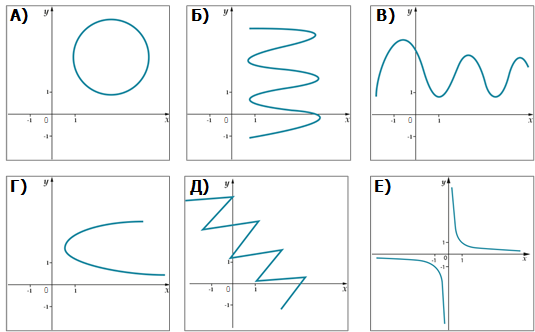
Проверим твои знания на практике. Определи по рисункам, что является функцией, а что нет:
Разобрался? А вот и ответы:
- Функцией является – В, Е.
- Функцией не является – А, Б, Г, Д.
Почему? Да вот почему:
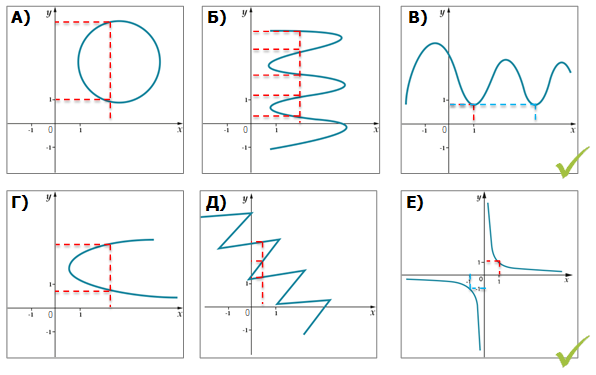
На всех рисунках кроме В) и Е) на один \( \displaystyle x\) приходится несколько \( \displaystyle y\)!
Уверена, теперь ты с легкостью отличишь функцию от «НЕ функции», скажешь, что такое аргумент и что такое зависимая переменная, а так же определишь область допустимых значений аргумента и область определения функции.
Приступаем к следующему разделу – как задать функцию?
4 способа задать функцию
Задать функцию — это значит определить правило, по которому по значениям переменной можно найти ее значения.
- Аналитический способ — с помощью формул. Очень удобно, потому что сжато и можно все быстро посчитать, подставляя значения в формулу.
- Табличный способ — более наглядный чем аналитический, но есть свои недостатки.
- Графический способ — самый наглядный. На графике сразу видно возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума.
- Словесный способ — самый понятный для не матиматиков.
Разберемся во всем по порядку, а начнем с аналитического способа.
Аналитический способ заданий функции
Аналитический способ – это и есть задание функции с помощью формулы. Это самый универсальный и исчерпывающий и однозначный способ.
Если у тебя есть формула, то ты знаешь о функции абсолютно все – ты можешь составить по ней табличку значений, можешь построить график, определить, где функция возрастает, а где убывает, в общем, исследовать ее по полной программе.
Рассмотрим функцию \( \displaystyle f\left( x \right)={{x}^{3}}-3{{x}^{2}}+{x}-2\). Чему равно \( \displaystyle f\left( 2 \right)\)?
«Что это значит?» – спросишь ты. Сейчас объясню.
Напомню, что в записи \( \displaystyle f(x)\) выражение в скобках называется аргументом.
И этот аргумент может быть любым выражением, не обязательно просто \( \displaystyle x\). Соответственно, каким бы ни был аргумент (выражение в скобках), мы его запишем вместо \( \displaystyle x\) в выражении \( \displaystyle f(x)\).
В нашем примере получится так:
\( \displaystyle f\left( 2 \right)={{2}^{3}}-3\cdot {{2}^{2}}+2-2=8-12+2-2=-4\).
Пример из ЕГЭ
Найдите значение выражения \( \displaystyle \frac{f\left( x-15 \right)}{f\left( x-18 \right)}\), при \( \displaystyle f\left( x \right)={{5}^{x}}\).
Уверена, что сначала ты испугался, увидев такое выражение, но в нем нет абсолютно ничего страшного!
Давай решим.
Все как и в прошлом примере: каким бы ни был аргумент (выражение в скобках), мы его запишем вместо \( \displaystyle x\) в выражении \( \displaystyle f(x)\). Например, для функции \( \displaystyle f\left( x \right)={{5}^{x}}:f\left( x+1 \right)={{5}^{\left( x+1 \right)}}\) .
Что же нужно сделать в нашем примере? Вместо \( \displaystyle f\left( x-15 \right)\) надо написать \( \displaystyle {{5}^{x-15}}\), а вместо – \( \displaystyle f\left( x-18 \right)-{{5}^{x-18}}\):
\( \displaystyle \frac{f\left( x-15 \right)}{f\left( x-18 \right)}=\frac{{{5}^{x-15}}}{{{5}^{x-18}}}\)
А дальше, используя свойства степени (можешь лишний раз одним глазком заглянуть в соответствующую тему – не помешает), а именно:
\( \displaystyle \frac{{{a}^{x}}}{{{a}^{y}}}={{a}^{x-y}}\) и \( \displaystyle {{a}^{x+y}}={{a}^{x}}\cdot {{a}^{y}}\)
сократить получившееся выражение:
\( \displaystyle \frac{f\left( x-15 \right)}{f\left( x-18 \right)}=\frac{{{5}^{x-15}}}{{{5}^{x-18}}}={{\left( \frac{{{5}^{x}}\cdot {{5}^{-15}}}{{{5}^{x}}\cdot {{5}^{-18}}} \right)}^{:{{5}^{x}}}}=\frac{{{5}^{18}}}{{{5}^{15}}}={{5}^{3}}=125\)
Вот и все!
Теперь попробуй самостоятельно найти значение следующих выражений:
- \( \displaystyle f\left( x-9 \right)+f\left( 16-x \right)\), если \( \displaystyle f\left( x \right)=3x+2\)
- \( \displaystyle 3f\left( x-4 \right)-f\left( 3x \right)\), если \( \displaystyle f\left( x \right)=x-5\)
Справился? Сравним наши ответы:
- \( \displaystyle 25\)
- \( \displaystyle -22\)
Мы привыкли, что функция имеет вид \( \displaystyle y=f\left( x \right)\), даже в наших примерах мы задаем функцию именно таким образом, однако аналитически можно задать функцию в неявном виде, например \( \displaystyle 5x+2y-3=0\). Попробуй построить эту функцию самостоятельно.
Справился?
Вот как строил ее я.
\( \displaystyle 5x+2y-3=0\)
\( \displaystyle y=\frac{3-5x}{2}\)
\( \displaystyle y=1,5-2,5x\)
Какое уравнение мы в итоге вывели? Правильно! Линейное, а это значит, что графиком будет прямая линия. Сделаем табличку, чтобы определить, какие точки принадлежат нашей прямой:
| \( \displaystyle x\) | \( \displaystyle 0\) | \( \displaystyle 1\) | \( \displaystyle -1\) | \( \displaystyle 2\) | \( \displaystyle -2\) |
| \( \displaystyle y\) | \( \displaystyle 1.5\) | \( \displaystyle -1\) | \( \displaystyle 4\) | \( \displaystyle -3.5\) | \( \displaystyle 6.5\) |
А теперь строим по данным точкам график:
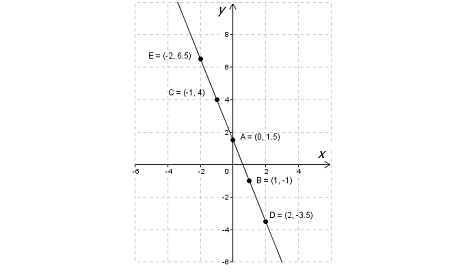
Вот так из неявной формулы получилась линейная функция.
А теперь посмотри следующую формулу: \( \displaystyle {{y}^{2}}=x\). Является ли она функцией? Согласись, вызывает затруднение…
Попробуй подставить различные значения \( \displaystyle x\) и посмотреть, какой \( \displaystyle y\) им соответствует.
| \( \displaystyle x\) | \( \displaystyle 0\) | \( \displaystyle 1\) | \( \displaystyle 4\) |
| \( \displaystyle y\) | \( \displaystyle 0\) | \( \displaystyle -1;1\) | \( \displaystyle -2;2\) |
Вот как раз то, о чем мы говорили… Одному \( \displaystyle x\) соответствует несколько \( \displaystyle y\). Попробуем нарисовать то, что получилось:
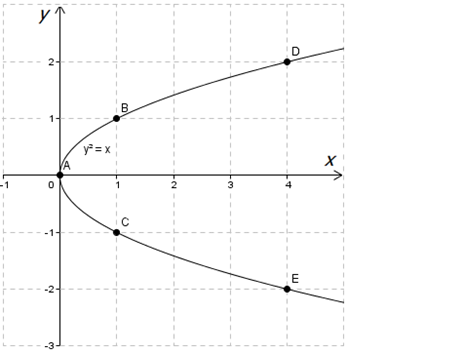
Является ли то, что у нас получилось функцией? Правильно, нет! Почему? Попробуй ответить на этот вопрос с помощью рисунка. Что у тебя вышло?
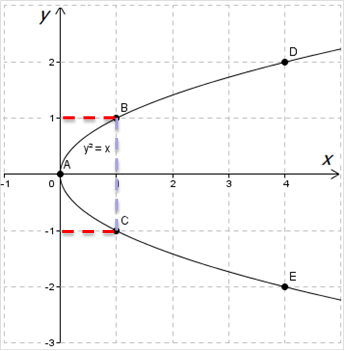
«Потому что одному значению \( \displaystyle x\) соответствует несколько значений \( \displaystyle y\)!»
Какой вывод мы можем из этого сделать?
Правильно, функция не всегда может быть выражена явно, и не всегда то, что «замаскировано» под функцию является функцией!
Табличный способ задания функции
Как следует из названия, этот способ представляет собой простую табличку. Да, да. Наподобие той, которой мы с тобой уже составляли. Например:
| \( \displaystyle x\) | \( \displaystyle 0\) | \( \displaystyle 1\) | \( \displaystyle -1\) | \( \displaystyle 2\) | \( \displaystyle -2\) |
| \( \displaystyle y\) | \( \displaystyle 4\) | \( \displaystyle -6\) | \( \displaystyle 3\) | \( \displaystyle -4\) | \( \displaystyle 15\) |
Как ты уже знаешь, в первой строчке мы ставим значение аргумента, а во второй строчке – соответствующие ему значение функции. Таким образом, в таблице каждому иксу соответствует одно значение игрека.
Заметь, в последней приведенной табличке невозможно четко определить правило, по которому игрек зависит от икс. Так тоже бывает и в этом нет ничего страшного, просто мы не можем вот так сразу взять и определить правило.
Если тебя это смущает, приведу в пример другую таблицу:
| \( \displaystyle x\) | \( \displaystyle 0\) | \( \displaystyle 1\) | \( \displaystyle -1\) | \( \displaystyle 2\) | \( \displaystyle -2\) |
| \( \displaystyle y\) | \( \displaystyle 0\) | \( \displaystyle 3\) | \( \displaystyle -3\) | \( \displaystyle 6\) | \( \displaystyle -6\) |
Здесь ты сразу подметил закономерность – игрек в три раза больше чем икс.
А теперь задание на «очень хорошо подумать»: как ты считаешь, равносильная ли функция, заданная в виде таблицы, функции \( \displaystyle y=3x\)?
Не будем долго рассуждать, а будем рисовать!
Итак. Рисуем функцию, заданную обоими способами:
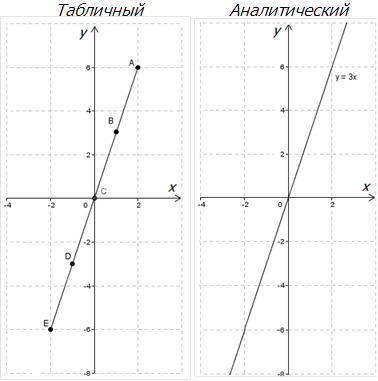
Видишь разницу? Дело совсем не в отмеченных точках! Присмотрись внимательнее:
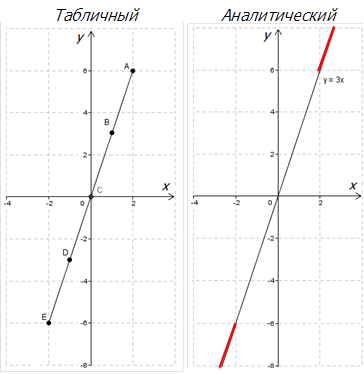
Теперь увидел? Когда мы задаем функцию табличным способом, мы на графике отражаем только те точки, которые есть у нас в таблице и линия (как в нашем случае) проходит только через них.
Когда мы задаем функцию аналитическим способом, мы можем взять любые точки, и наша функция ими не ограничивается. Вот такая вот особенность. Запоминай!
Графический способ построения функции
Графический способ построения функции не менее удобен. Мы рисуем нашу функцию, а другой заинтересованный человек может найти чему равен игрек при определенном икс и так далее.
Графический и аналитический способы одни из самых распространенных.
Однако, здесь нужно помнить о чем мы с тобой говорили в самом начале – не каждая «загогулина» нарисованная в системе координат является функцией! Вспомнил? На всякий случай скопирую тебе сюда определение, что функцией является:
Функцией называется правило \( \displaystyle f\), по которому каждому элементу \( \displaystyle x\) множества \( \displaystyle X\) ставится в соответствие единственный элемент \( \displaystyle y\) множества \( \displaystyle Y\) .
Как правило, люди обычно называют именно те три способа задания функции, которые мы разобрали – аналитический (с помощью формулы), табличный и графический, напрочь забывая о том, что функцию можно словесно описать.
Как это? Да очень просто!
Словесный способ задания функции
Как же описать функцию словесно?
Возьмем наш недавний пример – \( \displaystyle y=3x\).
Данную функцию можно описать «каждому действительному значению икс соответствует его утроенное значение». Вот и все. Ничего сложного.
Ты, конечно, возразишь: «Есть настолько сложные функции, которые словесно задать просто невозможно!» Да, есть и такие, но есть функции, которые описать словесно легче, чем задать формулой.
Например: «каждому натуральному значению икс соответствует разница между цифрами, из которых он состоит, при этом за уменьшаемое берется наибольшее цифра, содержащиеся в записи числа».
Теперь рассмотрим, как наше словесное описание функции реализуется на практике:
Пусть \( \displaystyle x=256\)
Наибольшая цифра в данном числе – \( \displaystyle 6\), соответственно, \( \displaystyle 6\) – уменьшаемое, тогда:
\( \displaystyle y=6-5-2=-1\).
Основные виды функций
Теперь перейдем к самому интересному – рассмотрим основные виды функций, с которыми ты работал/работаешь и будешь работать в курсе школьной и институтской математики, то есть познакомимся с ними, так сказать и дадим им краткую характеристику.
А еще будет полезно узнать про то, как строятся графики функций. Загляни сюда:
- Построение графика линейной функции
- Построение графика квадратичной функции
- Построение графика обратной зависимости
Линейная функция
Функция вида \( \displaystyle y=kx+b\), где \( \displaystyle k\), \( \displaystyle b\) – действительные числа.
Графиком данной функции служит прямая, поэтому построение линейной функции сводится к нахождению координат двух точек.
Положение прямой на координатной плоскости зависит от углового коэффициента \( \displaystyle k=tg\alpha \).
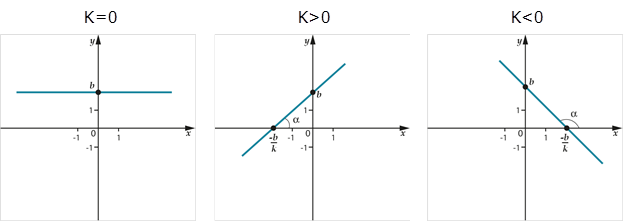
Область определения функции (aka область допустимых значений аргумента) – \( \displaystyle D\left( y \right)-\mathbb{R}\).
Область значений – \( \displaystyle E\left( y \right)-\mathbb{R}\).
Квадратичная функция
Функция вида \( \displaystyle y=a{{x}^{2}}+bx+c\), где \( \displaystyle a\ne 0\)
Графиком функции является парабола, при \( \displaystyle a<0\) ветви параболы направлены вниз, при \( \displaystyle a>0\) — вверх.
Многие свойства квадратичной функции зависят от значения дискриминанта. Дискриминант вычисляется по формуле \( \displaystyle D={{b}^{2}}-4ac\)
Положение параболы на координатной плоскости относительно значения \( \displaystyle D\) и коэффициента \( \displaystyle a\) показаны на рисунке:
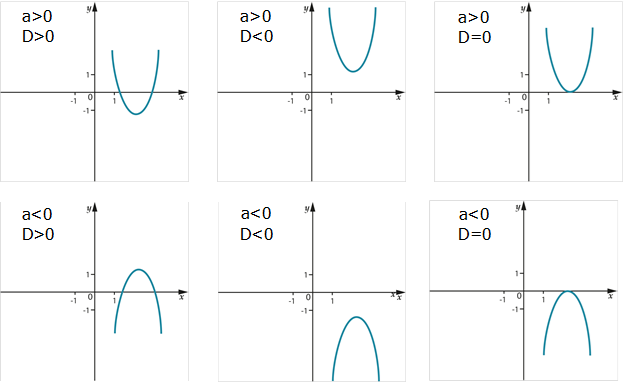
Область определения – \( \displaystyle D\left( y \right)=\mathbb{R}\)
Область значений \( \displaystyle E\left( y \right)\) зависит от экстремума данной функции (точки вершины параболы) и коэффициента \( \displaystyle a\) (направления ветвей параболы)
Обратная пропорциональность
Функция, задаваемая формулой \( \displaystyle y=\frac{k}{x}\), где \( \displaystyle k\ne 0\)
Число \( \displaystyle k\) называется коэффициентом обратной пропорциональности.
В зависимости от того, какое значение \( \displaystyle k\), ветви гиперболы находятся в разных квадратах:
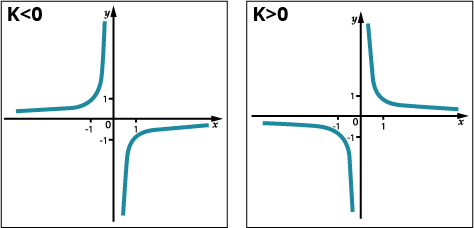
Область определения – \( \displaystyle D\left( y \right)-\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\).
Область значений – \( \displaystyle E\left( y \right)-\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\).
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)
Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.
Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики.
На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях).
Мы рассмотрим:
- степенную функцию (линейную, квадратичную, обратную зависимость, корни),
- тригонометрические и обратные тригонометрические,
- показательную и
- логарифмическую функции.
Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



следующих выражений:
f(x−9)+f(16−x), если f(x)=3x+2
добрый день! тут нет решения и я так и не поняла куда что подставлять, как степень? и как это тогда решается?!
Жулдуз, это самостоятельная работа, поэтому я привёл только ответы. Эту задачу нужно решать подобно предыдущей разобранной задаче.
Вместо х в функцию f(x)=3x+2 вместо х подставляем то, что написано в скобках:
f(x−9) = 3(x-9) + 2 = … (раскрываем скобки).
f(16−x) = 3(16-х) + 2 = …
Получившиеся выражения складываем, приводим подобные и получаем ответ.
Попробуйте самостоятельно доделать.
Здравствуйте, а можете пожалуйста прояснить, в первом примере появляется символ U: [-2;2] U [2;6]. Что он обозначает? Почему нельзя просто написать [-2;6].
Добрый день, Кристина. Тут все просто, двойка не входит в область определения. На рисунке это видно. Она как бы «выколота», посмотрите. Поэтому писать так, как вы нельзя. И поэтому область определения обозначена у нас КРУГЛЫМИ СКОБКАМИ, а не квадратными.
Чем квадратные скобки отличаются от круглых?
Круглая скобка означает, что число НЕ входит в область определения, квадратная – входит. При наличии бесконечности принято изображать круглую скобку. Дальше, если интересно про круглые и квадратные скобки смотрите здесь: https://ru.wikipedia.org/wiki/Скобки
Добрый день, ребенок в 7 классе. Подскажите, есть ли возможность изучать ваш учебник? На каких условиях? Как можно заниматься 7-8 классам?
Наталья, спасибо за интерес к учебнику. По учебнику можно заниматься почти с любого возраста. У нас есть пятиклассник, который занимается по учебнику с мамой. Потому что он написан от простого к сложному, как мы говорим, человеческим языком, и если тему в 7-8-м классе проходят, то заходите в содержание учебника https://youclever.org/book, открывайте нужную тему, читайте и решайте задачи.
Мы пока не продаем полный доступ к нему, но возможно вернемся к этому со следующего учебного года, потому что его постоянно просят вернуть… Я вам на почту пришлю персональное предложение, по поводу учебника. Посмотрите.
Почему в задаче на обл опр под номером 2 идет промежуток (6,2)? Надо наоборот.
Юлия, спасибо за комментарий и внимательность! Исправили. Действительно, нужно в промежутках идти от меньшего к большему. 🙂
Отличная статья
Спасибо, Маша! Заходите еще! )
Некоторые отзывы на эту статью за прошлые годы:
ВЛАД,10КЛАСС
23 октября 2017
Тому кто написал данную статью большое спасибо.Побольше бы таких людей.Вы мне очень помогли!!!СПАСИБО.
Anastira
29 марта 2018
Здравствуйте) Очень полезная статья, помогло разобраться с тем, чего я не понимала Но разве в разделе «Квадратичная функция» на 4, 5, 6 рисунке а > 0?
Светланаа
08 августа 2018
Очень хорошая у вас статья — даже инженеру в помощь!!!
Кристина
20 августа 2018
Спасибо огромное, очень доступно. А скажите,будь ласка, как найти аналитическую формулу функции по ее табличному виду, без подбора. Благодарю.
Марина
19 октября 2018
У меня скоро экзамен, недавно писала пробник, написала плохо, никогда не понимала функции, сейчас села, нашла эту статью, все переписала, попробовала решить и все получилось. У меня улыбка до ушей, спасибо огромное
Артемий
04 февраля 2019
Статья написана классно как всегда, но очень много важных моментов скрыто. И по этой причине не могу сказать что статья хорошая (но все равно лучше чем 90% всех тех что можно найти в инете). Откройте плиз область «Рассмотрим еще задание, связанное с аналитическим способом задания функции, которое будет у тебя на экзамене». Хотя бы один пример.