Однородные неравенства — способы решения
Неравенства зачем-то разделили на группы: однородные, рациональные, иррациональные, логарифмические, показательные.
Зачем?!
Чтобы было легче их решать! Ведь каждый тип неравенств имеет свой алгоритм и свои особенности решения. Пойми какое неравенство перед тобой, используй правильный алгоритм и дело в шляпе!
В этой статье разберем однородные неравенства.
Поехали!
Что такое однородное неравенство
Заметь, что определение однородного неравенства точно такое же как определение однородного уравнения, только знак другой (\( \displaystyle >,\ \ <,\ \ \ge ,\ \ \ \le \) вместо \( \displaystyle =\)).
Если ты не читал раздел «Однородные уравнения», то рекомендуем тебе это сделать. Там мы более подробно разобрались с этой громоздкой формулой, данной в определении.
Итак…
Определение однородного неравенства
Однородным называется неравенство вида \( \displaystyle {{k}_{0}}{{x}^{n}}+{{k}_{1}}{{x}^{n-1}}y+{{k}_{2}}{{x}^{n-2}}{{y}^{2}}+…+{{k}_{n-1}}x{{y}^{n-1}}+{{k}_{n}}{{y}^{n}}\ge 0\) (вместо знака \( \displaystyle \ge \) может стоять любой знак неравенства), с двумя неизвестными, в каждом слагаемом которого одинаковая сумма степеней этих неизвестных.
Не будем надолго останавливаться на определении, повторим лишь основные моменты.
Основные моменты однородных неравенств
Допустим, у нас будет \( \displaystyle \ge \).
Вот мы и получили простое однородное неравенство:
\( \displaystyle -2{{x}^{2}}+3xy+5{{y}^{2}}\ge 0\)
Теперь давай попробуем его решить.
Пример №1
При каких значениях \( \displaystyle x\), верно неравенство:
\( \displaystyle -2{{x}^{2}}+3xy+5{{y}^{2}}\ge 0\)?
Принцип решения такой же, как и у однородных уравнений – свести все к простому квадратному неравенству, и решить его (Повтори как решать «Квадратные неравенства»).
Для решения нам нужно разделить неравенство на \( {{y}^{2}}\ge 0\). Но как ты помнишь, здесь есть нюанс – на ноль делить нельзя.
Поэтому давай отдельно рассмотрим случай когда \( \displaystyle {{y}^{2}}=0\), т.е. \( \displaystyle y=0\):
\( \displaystyle -2{{x}^{2}}\ge 0\)
\( \displaystyle 2{{x}^{2}}\le 0\)
\( \displaystyle {{x}^{2}}\le 0\)
Но \( \displaystyle {{x}^{2}}\) не может быть отрицательным, а значит, это возможно только при \( \displaystyle {{x}^{2}}= 0\). Итак, при \( \displaystyle y=0: x=0\).
Теперь остались только \( \displaystyle y>0\). Можно смело делить:
\( \displaystyle \frac{-2{{x}^{2}}}{{{y}^{2}}}+\frac{3xy}{{{y}^{2}}}+\frac{5{{y}^{2}}}{{{y}^{2}}}\ge 0\)
\( \displaystyle -2{{\left( \frac{x}{y} \right)}^{2}}+3\left( \frac{x}{y} \right)+5\ge 0\)
Произведем замену \( \displaystyle t=\frac{x}{y}\) и решим простое квадратное неравенство:
\( \displaystyle -2{{t}^{2}}+3t+5\ge 0\)
Найдем корни уравнения \( \displaystyle -2{{t}^{2}}+3t+5=0\):
\( \displaystyle D={{b}^{2}}-4ac={{3}^{2}}-4\cdot \left( -2 \right)\cdot 5=9+40=49\)
\( \displaystyle t=\frac{-b\pm \sqrt{D}}{2a}=\frac{-3\pm \sqrt{49}}{2\cdot \left( -2 \right)}=\frac{-3\pm 7}{-4}\Rightarrow \left[ \begin{array}{l}{{t}_{1}}=\frac{10}{4}\\{{t}_{2}}=-1\end{array} \right.\Rightarrow\left[ \begin{array}{l}{{t}_{1}}=2,5\\{{t}_{2}}=-1\end{array} \right.\)
Отметим точки на прямой, и расставим знаки, учитывая, что ветви параболы направлены вниз (коэффициент \( \displaystyle a=-2\) при \( \displaystyle {{x}^{2}}\)):
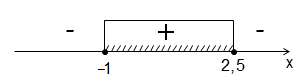
Таким образом, \( \displaystyle -1\le t\le 2,5\).
Произведем обратную замену:
\( \displaystyle -1\le \frac{x}{y}\le 2,5\)
\( \displaystyle -y\le x\le 2,5y\)
Поскольку y может быть как положительным, так и отрицательным, то нужно учесть это в ответе. При положительном у, значениеи \( \displaystyle -y\) будет меньше, чем \( \displaystyle 2,5y\), – а значит ответ записан корректно.
При отрицательном \( \displaystyle y\), наоборот, \( \displaystyle -y\) будет больше, чем \( \displaystyle 2,5y\). То есть:
При \( \displaystyle y<0:\ \ 2,5y\le x\le -y\)
Ответ:
При \( \displaystyle y<0\): \( \displaystyle 2,5y\le x\le -y\)
При \( \displaystyle y=0\): \( \displaystyle x=0\)
При \( \displaystyle y>0\): \( \displaystyle -y\le x\le 2,5y\)
Показательные однородные неравенства
Чаще всего однородные неравенства бывают показательными. Если ты забыл, как решаются показательные неравенства, повтори соответствующий раздел теории.
Давай рассмотрим несколько примеров.
Пример №2
Решите неравенство \( \displaystyle {{5}^{x}}-{{3}^{x}}\ge 0\)
Да-да! Это тоже однородное неравенство. Есть две переменных переменные (в виде \( \displaystyle {{5}^{x}}\) и \( \displaystyle {{3}^{x}}\)) и суммах их степеней в каждом слагаемом равна \( \displaystyle 1\).
Разделим все на \( \displaystyle {{3}^{x}}\). Важно заметить, что в показательных однородных неравенствах можно смело делить на переменную, ведь она всегда строго больше \( \displaystyle 0\) (\( \displaystyle {{3}^{x}}\) при любом \( \displaystyle x\) будет больше \( \displaystyle 0\)).
\( \displaystyle \begin{array}{l}\frac{{{5}^{x}}}{{{3}^{x}}}-\frac{{{3}^{x}}}{{{3}^{x}}}\ge 0\\{{\left( \frac{5}{3} \right)}^{x}}\ge 1\end{array}\)
А теперь все совсем просто. Представим \( \displaystyle 1\), как \( \displaystyle {{\left( \frac{5}{3} \right)}^{0}}\) и найдем \( \displaystyle x\):
\( \displaystyle \begin{array}{l}{{\left( \frac{5}{3} \right)}^{x}}\ge {{\left( \frac{5}{3} \right)}^{0}}\\x\ge 0\end{array}\)
Ответ: \( \displaystyle \left[ 0;\ \infty \right)\)
Рассмотрим еще несколько стандартных примеров, часто встречающихся в ЕГЭ.
Пример №3
Решите неравенство \( \displaystyle 2\cdot {{5}^{2x}}+{{10}^{x}}-15\cdot {{2}^{2x}}\le 0\)
Заметим, что \( \displaystyle {{10}^{x}}={{5}^{x}}\cdot {{2}^{x}}\).
Таким образом, перед нами однородное неравенство. Разделим все на \( \displaystyle {{2}^{2x}}\) (можно делить и на \( \displaystyle {{5}^{2x}}\) — сделай самостоятельно):
\( \displaystyle \begin{array}{l}\frac{2\cdot {{5}^{2x}}}{{{2}^{2x}}}+\frac{{{5}^{x}}\cdot {{2}^{x}}}{{{2}^{2x}}}-\frac{15\cdot {{2}^{2x}}}{{{2}^{2x}}}\le 0\\2\cdot {{\left( \frac{5}{2} \right)}^{2x}}+{{\left( \frac{5}{2} \right)}^{x}}-15\le 0\end{array}\)
Произведем замену \( \displaystyle t={{\left( \frac{5}{2} \right)}^{x}}>0\) и решим квадратное неравенство:
\( \displaystyle 2\cdot {{t}^{2}}+t-15\le 0\).
Найдем корни уравнения \( \displaystyle 2\cdot {{t}^{2}}+t-15=0\):
\( \displaystyle \begin{array}{l}D={{b}^{2}}-4ac={{1}^{2}}-4\cdot 2\cdot \left( -15 \right)=1+120=121\\t=\frac{-b\pm \sqrt{D}}{2a}=\frac{-1\pm 11}{2\cdot 2}=\frac{-1\pm 11}{4}=\left[ \begin{array}{l}{{t}_{1}}=2,5\\{{t}_{2}}=-3\end{array} \right.\end{array}\)
Отметим на прямой точки \( \displaystyle {{t}_{1}}\) и \( \displaystyle {{t}_{2}}\) и расставим знаки (ветви параболы направлены вверх, так как коэффициент \( \displaystyle a\) при \( \displaystyle {{t}_{2}}\) больше \( \displaystyle 0\)):
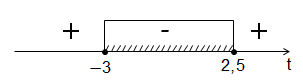
С учетом ОДЗ (\( \displaystyle t={{\left( \frac{5}{2} \right)}^{x}}>0\)) — \( \displaystyle 0\le t\le 2,5\).
Произведем обратную замену:
\( \displaystyle \begin{array}{l}0\le {{\left( \frac{5}{2} \right)}^{x}}\le 2,5\\0\le {{\left( \frac{5}{2} \right)}^{x}}\le {{\left( \frac{5}{2} \right)}^{1}}\end{array}\)
Поскольку \( \displaystyle {{\left( \frac{5}{2} \right)}^{x}}>0\) при любом \( \displaystyle x\), получаем ответ:
Ответ: \( \displaystyle \left( -\infty \ ;\ 1 \right]\)
Пример №4
Решите неравенство \( \displaystyle {{2}^{2x+1}}-5\cdot {{8}^{x}}+2\cdot {{4}^{2x}}<0\)
Заметим, что \( \displaystyle {{2}^{2x+1}}=2\cdot {{2}^{2x}}\), а \( \displaystyle {{8}^{x}}={{2}^{x}}\cdot {{4}^{x}}\).
Таким образом, перед нами однородное неравенство.
Разделим его на \( \displaystyle {{4}^{2x}}\):
\( \displaystyle \begin{array}{l}\frac{2\cdot {{2}^{2x}}}{{{4}^{2x}}}-\frac{5\cdot {{2}^{x}}\cdot {{4}^{x}}}{{{4}^{2x}}}+\frac{2\cdot {{4}^{2x}}}{{{4}^{2x}}}<0\\2\cdot {{\left( \frac{2}{4} \right)}^{2x}}-5\cdot {{\left( \frac{2}{4} \right)}^{x}}+2<0\\2\cdot {{\left( \frac{1}{2} \right)}^{2x}}-5{{\left( \frac{1}{2} \right)}^{x}}+2<0\end{array}\)
Произведем замену \( \displaystyle t={{\left( \frac{1}{2} \right)}^{x}}>0\) и решим квадратное неравенство:
\( \displaystyle 2{{t}^{2}}-5t+2<0\).
Найдем корни уравнения \( \displaystyle 2{{t}^{2}}-5t+2=0\):
\( \displaystyle \begin{array}{l}D={{b}^{2}}-4ac={{\left( -5 \right)}^{2}}-4\cdot 2\cdot 2=25-16=9\\t=\frac{-b\pm \sqrt{D}}{2a}=\frac{-\left( -5 \right)\pm \sqrt{9}}{2\cdot 2}=\frac{5\pm 3}{4}=\left[ \begin{array}{l}{{t}_{1}}=2\\{{t}_{2}}=\frac{1}{2}\end{array} \right.\end{array}\)Отметим на прямой точки \( \displaystyle {{t}_{1}}\) и \( \displaystyle {{t}_{2}}\) и расставим знаки (ветви параболы направлены вверх, так как коэффициент \( \displaystyle a\) при \( \displaystyle {{t}_{2}}\) больше \( \displaystyle 0\)):
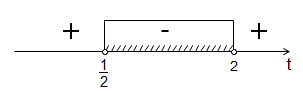
Таким образом, \( \displaystyle \frac{1}{2}<t<2\)
Произведем обратную замену: \( \displaystyle \begin{array}{l}\frac{1}{2}<{{\left( \frac{1}{2} \right)}^{x}}<2\\{{\left( \frac{1}{2} \right)}^{1}}<{{\left( \frac{1}{2} \right)}^{x}}<{{\left( \frac{1}{2} \right)}^{-1}}\end{array}\)
Поскольку основание \( \displaystyle \frac{1}{2}<1\), то при избавлении от дроби мы меняем знаки неравенства: \( \displaystyle -1<x<1\)
Ответ: \( \displaystyle \left( -1\ ;\ 1 \right)\)
Задания для самостоятельного решения
Задачи:
Ответы:
Неравенство с параметром
\( \displaystyle {{x}^{2}}-3ax+2{{a}^{2}}\le 0\), при \( \displaystyle a\ne 0\).
Его мы сможем решить с помощью метода интервалов, если разложим левую часть на множители. Но как это сделать?
Заметим, что если поделить каждое слагаемое на \( \displaystyle {{a}^{2}}\), получим:
\( \displaystyle {{x}^{2}}-3ax+2{{a}^{2}}\le 0\text{ }\left| :{{a}^{2}} \right.\text{ }\Leftrightarrow \)
\( \displaystyle \frac{{{x}^{2}}}{{{a}^{2}}}-\frac{3ax}{{{a}^{2}}}+\frac{2{{a}^{2}}}{{{a}^{2}}}\le 0\text{ }\Leftrightarrow \text{ }{{\left( \frac{x}{a} \right)}^{2}}-3\frac{x}{a}+2\le 0\)
Сделав замену \( \displaystyle t=\frac{x}{a}\), получим обычное квадратное неравенство относительно \( \displaystyle t\):
\( \displaystyle {{t}^{2}}-3t+2\le 0\text{ }\Leftrightarrow \text{ }\left( t-2 \right)\left( t-1 \right)\le 0\text{ }\Leftrightarrow \text{ 1}\le t\le 2\).
Обратная замена: \( \displaystyle 1\le \frac{x}{a}\le 2\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}a\le x\le 2a,\text{ } при \ \ a>0\\2a\le x\le a,\text{ } при \ \ a<0\end{array} \right.\)
Такие неравенства называются однородными.
| Однородным называется неравенство вида:\( \displaystyle {{k}_{0}}{{x}^{n}}+{{k}_{1}}{{x}^{n-1}}y+{{k}_{2}}{{x}^{n-2}}{{y}^{2}}+…+{{k}_{n-1}}x{{y}^{n-1}}+{{k}_{n}}{{y}^{n}}\ge 0\)(вместо знака \( \displaystyle \ge \) может, конечно, стоять любой знак неравенства). |
То есть это неравенство с двумя неизвестными, в каждом слагаемом которого одинаковая сумма степеней этих неизвестных. Например, в примере выше эта сумма равна \( \displaystyle 2\). Решаются такие неравенства делением на одну из неизвестных в этой степени:
\( \displaystyle {{k}_{0}}{{x}^{n}}+{{k}_{1}}{{x}^{n-1}}y+{{k}_{2}}{{x}^{n-2}}{{y}^{2}}+…+{{k}_{n-1}}x{{y}^{n-1}}+{{k}_{n}}{{y}^{n}}\le 0\text{ }\left| :{{y}^{n}}\text{ } \right.\Leftrightarrow \)\( \displaystyle {{k}_{0}}{{\left( \frac{x}{y} \right)}^{n}}+{{k}_{1}}{{\left( \frac{x}{y} \right)}^{n-1}}+{{k}_{2}}{{\left( \frac{x}{y} \right)}^{n-2}}+…+{{k}_{n-1}}\left( \frac{x}{y} \right)+{{k}_{n}}\le 0\),
и последующей заменой переменных: \( \displaystyle t=\frac{x}{y}\). Таким образом получаем рациональное неравенство \( \displaystyle n\)-ной степени с одной неизвестной \( \displaystyle t\):
\( \displaystyle {{k}_{0}}{{t}^{n}}+{{k}_{1}}{{t}^{n-1}}+{{k}_{2}}{{t}^{n-2}}+…+{{k}_{n-1}}t+{{k}_{n}}\le 0\).
Ты заметил ошибку в моих рассуждениях?
Ведь нельзя просто так взять и поделить неравенство на переменную! Она (переменная) может оказаться отрицательной или нулевой.
Поэтому всегда нужно специально проверять, можно ли это сделать.
Чаще всего нам будут встречаться неравенства второй степени (то есть квадратные), тогда делить придется на переменную в квадрате, а она заведомо неотрицательна:
\( \displaystyle a{{x}^{2}}+bxy+c{{y}^{2}}\ge 0\text{ }\left| :{{y}^{2}}\ne \text{0 }\Leftrightarrow \text{ }a{{\left( \frac{x}{y} \right)}^{2}}+b\cdot \frac{x}{y} \right.+c\ge 0\text{ }\underset{t=\frac{x}{y}}{\mathop{\Leftrightarrow }}\,\text{ }\)
\( \displaystyle \underset{t=\frac{x}{y}}{\mathop{\Leftrightarrow }}\,\text{ }a{{t}^{2}}+bt+c\ge 0 \)
Отметим также, что эта переменная не может быть равна нулю. В случаях, когда это не очевидно, необходимо отдельно проверять случай когда эта переменная равна нулю. Например:
Решите неравенство \( \displaystyle {{x}^{2}}-3ax+2{{a}^{2}}\le 0\) при всех \( \displaystyle a\).
Пример №5
Видим здесь типичное однородное неравенство: \( \displaystyle x\) и \( \displaystyle a\) – это неизвестные, а сумма их степеней в каждом слагаемом равна \( \displaystyle 2\).
Но, прежде чем разделить на \( \displaystyle {{a}^{2}}\) и получить квадратное неравенство относительно \( \displaystyle \frac{x}{a}\), мы должны рассмотреть случай, когда \( \displaystyle a=0\). В этом случае неравенство примет вид: \( \displaystyle {{x}^{2}}\le 0\), значит, \( \displaystyle x=0\) – решение неравенства при \( \displaystyle a=0\).
А теперь пусть \( \displaystyle a\ne 0\), тогда и \( \displaystyle {{a}^{2}}\ne 0\), и на него можно смело делить:
\( \displaystyle {{x}^{2}}-3ax+2{{a}^{2}}\le 0\text{ }\left| :{{a}^{2}} \right.\text{ }\Leftrightarrow \)
\( \displaystyle \frac{{{x}^{2}}}{{{a}^{2}}}-\frac{3ax}{{{a}^{2}}}+\frac{2{{a}^{2}}}{{{a}^{2}}}\le 0\text{ }\Leftrightarrow \text{ }{{\left( \frac{x}{a} \right)}^{2}}-3\frac{x}{a}+2\le 0\)
Замена \( \displaystyle t=\frac{x}{a}\):
\( \displaystyle {{t}^{2}}-3t+2\le 0\text{ }\Leftrightarrow \text{ }\left( t-2 \right)\left( t-1 \right)\le 0\text{ }\Leftrightarrow \text{ 1}\le t\le 2\).
Обратная замена: \( \displaystyle 1\le \frac{x}{a}\le 2\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}a\le x\le 2a,\text{ } при \ \ a>0\\2a\le x\le a,\text{ } при \ \ a<0\end{array} \right.\)
Ответ:
\( \displaystyle 0\) при \( \displaystyle a=0\);
\( \displaystyle \left[ a;2a \right]\) при \( \displaystyle a>0\)
\( \displaystyle \left[ 2a;a \right]\) при \( \displaystyle a<0\)
Чаще всего однородные неравенства нам попадаются среди показательных. Помнишь, как они решаются? Чтобы их вспомнить, посмотри тему «Показательные неравенства».
Пример №6
\( \displaystyle {{3}^{x}}-{{2}^{x}}\ge 0\).
Неужели это простое неравенство так сложно называется – однородное?
Да, однородные неравенства чаще всего довольно простые. Действительно, здесь в качестве переменных \( \displaystyle {{3}^{x}};\text{ }{{2}^{x}}\), и в каждом слагаемом сумма их степеней одинакова: \( \displaystyle 1\).
Итак, на что делим?
\( \displaystyle {{3}^{x}}-{{2}^{x}}\ge 0\text{ }\left| :{{2}^{x}}>0\text{ }\Leftrightarrow \text{ }{{\left( \frac{3}{2} \right)}^{x}}-1\ge 0\text{ }\Leftrightarrow \text{ } \right.{{\left( \frac{3}{2} \right)}^{x}}\ge 1\text{ }\Leftrightarrow \text{ }x\ge 0\).
Как видим, в показательных неравенствах ничего дополнительно проверять не нужно – все и так всегда строго положительно.
Задания для самостоятельного решения
Если примеры совсем не даются, повтори темы «Квадратные неравенства» и «Показательные неравенства».
Пример №7
\( \displaystyle {{3}^{2x}}-2\cdot {{2}^{x}}\cdot {{3}^{x}}+{{2}^{2x}}\le 0\text{ }\Leftrightarrow \) \( \displaystyle \Leftrightarrow \text{ }{{\left( {{3}^{x}} \right)}^{2}}-2\cdot {{2}^{x}}\cdot {{3}^{x}}+{{\left( {{2}^{x}} \right)}^{2}}\le 0\text{ }\left| :{{\left( {{2}^{x}} \right)}^{2}}>0 \right.\text{ }\Leftrightarrow \) \( \displaystyle {{\left( \frac{{{3}^{x}}}{{{2}^{x}}} \right)}^{2}}-2\cdot \frac{{{3}^{x}}}{{{2}^{x}}}+1\le 0\text{ }\underset{t={{\left( \frac{3}{2} \right)}^{x}}>0}{\mathop{\Leftrightarrow }}\,\text{ }{{t}^{2}}-2t+1\le 0\text{ }\Leftrightarrow \text{ }\) \( \displaystyle \Leftrightarrow \text{ }{{\left( t-1 \right)}^{2}}\le 0\text{ }\Leftrightarrow \text{ }t=1\text{ }\Leftrightarrow \text{ }x=0\)Пример №8
\( \displaystyle 10\cdot {{5}^{2x}}-29\cdot {{10}^{x}}+10\cdot {{2}^{2x}}\le 0\text{ }\Leftrightarrow \)
\( \displaystyle \Leftrightarrow \text{ }10\cdot {{5}^{2x}}-29\cdot {{2}^{x}}\cdot {{5}^{x}}+10\cdot {{2}^{2x}}\le 0\text{ }\left| :{{2}^{2x}}>0\text{ }\Leftrightarrow \right.\)
\( \displaystyle \Leftrightarrow 10\cdot {{\left( \frac{5}{2} \right)}^{2x}}-29\cdot {{\left( \frac{5}{2} \right)}^{x}}+10\le 0\text{ }\underset{t={{\left( \frac{5}{2} \right)}^{x}}}{\mathop{\Leftrightarrow }}\,\text{ }10{{t}^{2}}-29t+10\le 0\text{ }\Leftrightarrow \text{ }\)
\( \displaystyle \Leftrightarrow 10\left( t-2,5 \right)\left( t-0,4 \right)\le 0\text{ }\Leftrightarrow \)
\( \displaystyle 0,4\le t\le 2,5\text{ }\Leftrightarrow \text{ }\frac{2}{5}\le {{\left( \frac{5}{2} \right)}^{x}}\le \frac{5}{2}\text{ }\Leftrightarrow \text{ }-1\le x\le 1\).
Ответ: \( \displaystyle \left[ -1;1 \right]\).
Пример №9
\( \displaystyle {{2}^{2x}}-3\cdot {{10}^{x}}+2\cdot {{5}^{2x}}>0\text{ }\left| :{{5}^{2x}}>0 \right.\text{ }\Leftrightarrow \)
\( \displaystyle \Leftrightarrow {{\left( \frac{2}{5} \right)}^{2x}}-3{{\left( \frac{2}{5} \right)}^{x}}+2>0\text{ }\underset{t={{\left( \frac{2}{5} \right)}^{x}}>0}{\mathop{\Leftrightarrow }}\,\text{ }{{t}^{2}}-3t+2>0\text{ }\Leftrightarrow \)
\( \displaystyle \left( t-1 \right)\left( t-2 \right)>0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}t>2\\0<t<1\end{array} \right.\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}{{\left( \frac{2}{5} \right)}^{x}}>2\\0<{{\left( \frac{2}{5} \right)}^{x}}<1\end{array} \right.\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}x<{{\log }_{\frac{2}{5}}}2\\x>0.\end{array} \right.\)
Ответ:
\( \displaystyle \left( -\infty ;{{\log }_{\frac{2}{5}}}2 \right)\cup \left( 0;+\infty \right)\).
Шпаргалка по однородный неравенствам
Однородным называется неравенство вида \( \displaystyle {{k}_{0}}{{x}^{n}}+{{k}_{1}}{{x}^{n-1}}y+{{k}_{2}}{{x}^{n-2}}{{y}^{2}}+…+{{k}_{n-1}}x{{y}^{n-1}}+{{k}_{n}}{{y}^{n}}\ge 0\)
(вместо знака \( \displaystyle \ge \) может, конечно, стоять любой знак неравенства).
Алгоритм решения однородных неравенств
Чаще всего будут встречаться неравенства второй степени, тогда делить придется на переменную в квадрате, а она заведомо неотрицательна:
\( \displaystyle a{{x}^{2}}+bxy+c{{y}^{2}}\ge 0\text{ }\left| :{{y}^{2}}\ne \text{0 }\Leftrightarrow \text{ }a{{\left( \frac{x}{y} \right)}^{2}}+b\cdot \frac{x}{y} \right.+c\ge 0\text{ }\underset{t=\frac{x}{y}}{\mathop{\Leftrightarrow }}\,\text{ }a{{t}^{2}}+bt+c\ge 0\).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



В примере 1 при вычислении корней перепутаны знаки, т.к. в третьем вычислении потерян перед тройкой минус. А на координатную ось корни нанесены уже верно
Ирина, спасибо, опечатки исправил.