Рациональные неравенства
Привет!
Хочешь без труда решать ЛЮБЫЕ неравенства?
Тогда начни с рациональных! Они станут твоей крепкой опорой в решении других неравенств.
Читай эту статью и ты во всём разберешься!
Рациональные неравенства — коротко о главном
Определение рационального неравенства
Рациональное неравенство — неравенство, левая и правая части которого являются дробно-рациональными функциями, то есть функциями, представимыми в виде отношения многочленов \(\displaystyle f\left(x\right)\) и \(\displaystyle g\left(x\right)\).
Стандартный вид рационального неравенства
\(\displaystyle \frac{f\left(x\right)}{g\left(x\right)}>0\)
Строгие рациональные неравенства
- \(\displaystyle \frac{f\left(x\right)}{g\left(x\right)}>0\), тогда и только тогда, когда \(\displaystyle f\left(x\right)\cdot g\left(x\right)>0\);
- \(\displaystyle \frac{f\left(x\right)}{g\left(x\right)}<0\), тогда и только тогда, когда \(\displaystyle f\left(x\right)\cdot g\left(x\right)<0\).
Нестрогие рациональные неравенства
- \(\displaystyle \frac{f\left( x \right)}{g\left( x \right)}\ge 0\ \ \Leftrightarrow \ \ \left[ \begin{array}{l}\frac{f\left( x \right)}{g\left( x \right)}>0,\\\left\{ \begin{array}{l}f\left( x \right)=0,\\g\left( x \right)\ne 0.\end{array} \right.\end{array} \right.\)
- \(\displaystyle \frac{f\left( x \right)}{g\left( x \right)}\le 0\ \ \Leftrightarrow \ \ \left[ \begin{array}{l}\frac{f\left( x \right)}{g~\left( x \right)}<0,\\\left\{ \begin{array}{l}f\left( x \right)=0,\\g\left( x \right)\ne 0.\end{array} \right.\end{array} \right.\)
Алгоритм решения рациональных неравенств
- Переносим все в одну сторону и приводим к общему знаменателю, чтобы получить рациональное неравенство в стандартном виде: \(\displaystyle \frac{f\left(x\right)}{g\left(x\right)}>0\);
- Раскладываем числитель (\(\displaystyle f\left( x \right)\)) и знаменатель (\(\displaystyle g\left( x \right)\)) на множители. Для этого решаем уравнения \(\displaystyle f\left( x \right)=0\) и \(\displaystyle g\left( x \right)=0\);
- Находим ОДЗ (\(\displaystyle g\left( x \right)\ne 0\));
- Отмечаем на числовой оси нули числителя и нули знаменателя;
- Определяем знаки для каждого интервала. Для этого берем произвольный ???? из одного из интервалов и определяем знак в интервале к которому относится корень, чередуем знаки, обращая внимание на корни, повторяющиеся в неравенстве несколько раз, от четности или нечетности количества раз их повторения зависит, меняется знак при прохождении через них или нет;
- Выбираем интервалы, на которых значения функции имеют знак, соответствующий знаку неравенства;
- Записываем ответ, обращая внимания на знак неравенства и на ОДЗ. Если неравенство строгое — все точки выколотые; если неравенство нестрогое — нули знаменателя — выколотые точки (по ОДЗ), а нули числителя — не выколотые точки.
Рациональные неравенства — подробнее
Рациональные неравенства – это неравенства, обе части которых являются рациональными выражениями.
Что такое рациональное выражение? Напомню:
Рациональное выражение — это алгебраическое выражение, составленное из чисел и переменной \(\displaystyle x\) с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.
Например, такое рациональное неравенство: \(\displaystyle \frac{x+1}{{x}-2}\le \frac{x+2}{x}\)
Решение всех рациональных неравенств сводится к двум основным шагам:
Шаг 1. Перенос. Общий знаменатель. Разложение на множители
Переносим все в одну сторону, приводим к общему знаменателю и раскладываем числитель и знаменатель на множители.
Все множители должны быть «линейными», то есть переменная в каждом из них – только в первой степени.
Если какой-то из множителей нелинейный, и его невозможно разложить на линейные, от него надо избавиться.
Если забыл, как раскладывать выражение на множители, прочти тему «Разложение многочленов на множители».
Шаг 2. Метод интервалов
Если не знаешь, что это такое, прочти тему «Метод интервалов».
Первый шаг у нас уже раньше встречался. Где? В рациональных уравнениях!
Но в отличие от уравнений, в неравенствах мы никогда не разделяем числитель и знаменатель!
Более того, если в числителе и знаменателе есть одинаковые нечисловые множители, мы их не сокращаем!
Это правило у нас уже было в теме «Метод интервалов». И вообще, в этой теме мы уже учились решать рациональные неравенства. Поэтому здесь ограничимся отдельными примерами.
4 примера на рациональные неравенства
Пример №1
\(\displaystyle \frac{x}{{x}-2}\le 1\)Решение:
Очень распространенной ошибкой здесь будет домножить все на знаменатель.
Делать этого нельзя: мы ведь не знаем какой знак имеет выражение \(\displaystyle \left( {x}-2 \right)\); но при умножении на отрицательное число знак неравенства меняется! А на положительное – не меняется.
Так что, менять нам знак или нет? Лучше просто не умножать! Следуем нашим двум шагам: переносим все в одну сторону.
\(\displaystyle \frac{x}{{x}-2}\le 1\text{ }\Leftrightarrow \text{ }\frac{x}{{x}-2}-1\le 0\text{ }\Leftrightarrow \text{ }\frac{{x}-x+2}{{x}-2}\le 0\text{ }\Leftrightarrow \text{ }\frac{2}{{x}-2}\le 0\)
Почему корень выколотый? Потому что он из знаменателя!
\(\displaystyle x<2\)
Пример 2
\(\displaystyle \frac{x+1}{{x}-2}\le \frac{x+2}{x}\)Решение
\(\displaystyle \frac{x+1}{{x}-2}\le \frac{x+2}{x}\text{ }\Leftrightarrow \text{ }\frac{x+1}{{x}-2}-\frac{x+2}{x}\le 0\text{ }\Leftrightarrow \text{ }\) \(\displaystyle \frac{x\left( x+1 \right)-\left( x+2 \right)\left( {x}-2 \right)}{x\left( {x}-2 \right)}\le 0\text{ }\Leftrightarrow \) \(\displaystyle \frac{{{x}^{2}}+{x}-{{x}^{2}}+4}{x\left( {x}-2 \right)}\le 0\text{ }\Leftrightarrow \text{ }\frac{x+4}{x\left( {x}-2 \right)}\le 0\)
\(\displaystyle x\in \left( -\infty ;-4 \right]\cup \left( 0;2 \right)\)
Пример 3
\(\displaystyle \frac{{x}-2}{{{x}^{2}}+2{x}-3}-\frac{x+1}{{{x}^{2}}+5x+6}\le \frac{3}{x+3}\)Решение
Чтобы привести дроби к наименьшему общему знаменателю, разложим их знаменатели на множители.
Это квадратные трехчлены, надо вспомнить, как их раскладывают на множители? (подробное описание см. в разделе «Разложение на множители»).
Напомню, что для этого нужно найти корни соответствующих квадратных уравнений:
\(\displaystyle \begin{array}{l}{{x}^{2}}+2{x}-3=0\\{{x}^{2}}+5x+6=0\end{array}\)
Решим их с помощью теоремы Виета: у первого корни \(\displaystyle 1\) и \(\displaystyle -3\), у второго \(\displaystyle -2\) и \(\displaystyle -3\).
\(\displaystyle \begin{array}{l}\frac{{x}-2}{{{x}^{2}}+2{x}-3}-\frac{x+1}{{{x}^{2}}+5x+6}\le \frac{3}{x+3}\Leftrightarrow \\\Leftrightarrow \frac{{x}-{{2}^{\backslash x+2}}}{\left( {x}-1 \right)\left( x+3 \right)}-\frac{x+{{1}^{\backslash {x}-1}}}{\left( x+2 \right)\left( x+3 \right)}-\frac{{{3}^{\backslash \left( {x}-1 \right)\left( x+2 \right)}}}{x+3}\le 0\Leftrightarrow \\\Leftrightarrow \frac{{{x}^{2}}-4-\left( {{x}^{2}}-1 \right)-3\left( {{x}^{2}}+{x}-2 \right)}{\left( {x}-1 \right)\left( x+2 \right)\left( x+3 \right)}\le 0\Leftrightarrow \\\frac{-3{{x}^{2}}-3x+3}{\left( {x}-1 \right)\left( x+2 \right)\left( x+3 \right)}\le 0\Leftrightarrow \\\frac{{{x}^{2}}+{x}-1}{\left( {x}-1 \right)\left( x+2 \right)\left( x+3 \right)}\ge 0\end{array}\)
Для того, чтобы разложить на множители числитель, так же как и раньше, решим соответствующее квадратное уравнение:
\(\displaystyle \left. \begin{array}{l}{{x}^{2}}+{x}-1=0\\D=1+4=5\\{{x}_{1,2}}=\frac{-1\pm \sqrt{5}}{2}\text{ }\end{array} \right|\Rightarrow \text{ }{{x}^{2}}-{x}-1=\left( {x}-\frac{-1+\sqrt{5}}{2} \right)\left( {x}-\frac{-1-\sqrt{5}}{2} \right)\)
Вернемся к неравенству. Оно принимает вид:
\(\displaystyle \frac{\left( {x}-\frac{-1+\sqrt{5}}{2} \right)\left( {x}-\frac{-1-\sqrt{5}}{2} \right)}{\left( {x}-1 \right)\left( x+2 \right)\left( x+3 \right)}\ge 0\)
Теперь нужно расположить эти корни на числовой оси, а для этого надо понять, где находятся числа \(\displaystyle \frac{-1-\sqrt{5}}{2}\) и \(\displaystyle \frac{-1+\sqrt{5}}{2}\) относительно \(\displaystyle 1\), \(\displaystyle -2\) и \(\displaystyle -3\).
Подробно о том, как это делается, читай в теме «Сравнение чисел».
Пример 4
\(\displaystyle \frac{2{{x}^{2}}-2x}{{{x}^{2}}-x+1}<\frac{2{{x}^{2}}-2x-2}{{{x}^{2}}-{x}-2}-1\)Решение
Ты уже попробовал привести к общему знаменателю? Ужас, правда? Нужно что-то другое.
Но ты не мог не заметить, что куда ни посмотри, нам все время попадается одно и то же выражение \(\displaystyle \left( {{x}^{2}}-x \right)\).
А это верный знак, что сейчас будет замена переменных (повтори одноименную тему «Замена переменных»):
\(\displaystyle t={{x}^{2}}-x\)
Тогда наше неравенство принимает вид:
\(\displaystyle \frac{2t}{t+1}<\frac{2t-2}{t-2}-1\)
Такое мы решать уже умеем:
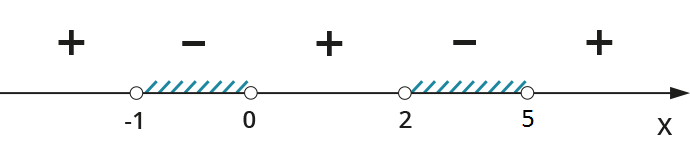
Не забываем вернуться к начальной переменной \(\displaystyle x\)!
Для этого нужно переписать полученное решение для \(\displaystyle t\) в виде неравенств:
Бонусы: Вебинары с нашего курса подготовки к ЕГЭ по математике
ЕГЭ 15. Решение уравнений и неравенств. Метод интервалов
В этом видео мы узнаем (вспомним) метод интервалов, поймём как и почему он работает.
Вспомним, как решать квадратные, рациональные неравенства, а также неравенства с модулем и иррациональные.
ЕГЭ 15. Смешанные неравенства. Логарифмические и тригонометрические
Задачу №15 мы на курсе уже научились решать: разобрали по косточкам и показательные, и логарифмические (в том числе с переменными основаниями), и смешанные неравенства.
Ну и системы неравенств не забыли. Бонусом прошлись по иррациональным неравенствам и неравенствам с модулем.
Но погодите, не выдыхайте пока. Поиграем в слабо!
А слабо скрестить логарифмы с тригонометрией? Этим и займемся в задаче на логарифмы с разными основаниями. Мы решим эту сложную задачу 2-мя способами!
Эти видео — вебинары, входящие в наш курс подготовки к ЕГЭ по математике.
По 15 задаче ЕГЭ мы также разберем как решать рациональные уравнения, уравнения с модулем, иррациональные уравнения системы уравнений с двумя неизвестными, рассмотрим тему сравнение чисел — корни.
Научившись решать отдельные неравенства, мы перейдем к системам неравенств и узнаем, как строится решение системы неравенств.
Все это нужно знать для решения 15-й задачи. Если вы будете готовиться к ЕГЭ самостоятельно, составьте план подготовки и включите в него все эти темы.
И не забудьте решить как можно больше задач по этим темам!
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org


