Показательные неравенства
В этой статье есть все о показательных неравенствах.
Для тех, кто ничего не знает, мы начнем с самых азов, с самых простейших примеров. И постепенно научим вам решать любые показательные неравенства, которые могут встретиться вам на ЕГЭ.
Если вы продвинутый школьник, вы можете пропустить азы и переходить сразу… к методу декомпозиции или к анализу монотонности функций. 🙂
А если серьезно, даже если вы уже хорошо знаете тему, вы точно найдете для себя что-то новое!
Или же хорошо потренируетесь, если решите все 44 неравенства этой статьи самостоятельно.
Показательные неравенства — коротко о главном
Определение:
Простейшими показательными неравенствами являются неравенства следующего вида:
\({{a}^{f\left( x \right)}}>{{a}^{g\left( x \right)}},~{{a}^{f\left( x \right)}}<{{a}^{g\left( x \right)}},~{{a}^{f\left( x \right)}}\ge {{a}^{g\left( x \right)}},~{{a}^{f\left( x \right)}}\le {{a}^{g\left( x \right)}}\),
Где \(a\) – основание, \(f\left( x \right),~g\left( x \right)\) – показатели.
Правило решения показательных неравенств:
\({{a}^{f\left( x \right)}}>{{a}^{g\left( x \right)}}=>~f\left( x \right)>g\left( x \right)\) \(\left(при\ ~a>1 \right)\)
\({{a}^{f\left( x \right)}}>{{a}^{g\left( x \right)}}=>~f\left( x \right)<g\left( x \right)\) \((при\ ~0<a<1)\)
Методы решения показательных неравенств:
- Метод группировки.
- Метод интервалов.
- Преобразование оснований.
- Разложение на множители.
- Замена переменной.
- Метод декомпозиции.
- Анализ монотонности функции.
Темы на повторение
- Вспомнить простейшие свойства степеней;
- Вспомнить, как решаются линейные неравенства и квадратичные неравенства;
- Вспомнить, как решаются показательные уравнения;
- Метод интервалов (будем разбирать в этой статье);
- Свойства логарифмов.
Показательные неравенства — самые азы
Этот раздел для тех, кто «ничего не знает» про показательные неравенства.
Начнем с самого начала, чтобы вы разобрались в базовых вещах и далее понимали что вы делаете. Обязательно решите все примеры самостоятельно!
Если вы продвинутый читатель, можете его пропустить. Но лучше просмотреть и решить все примеры.
Это займет у вас 5 минут.
Если \(\displaystyle {{5}^{x}}~=25\), то \(\displaystyle x=2\). А если \(\displaystyle 5x>25\), каким же должен быть \(\displaystyle x\)?
Я думаю, что ты без труда понял, что \(\displaystyle x>5\).
А если \(\displaystyle {{5}^{x}}~>25\ \)?
Так как \(\displaystyle 25={{5}^{2}}\), то ты вполне резонно можешь предположить, что \(\displaystyle x>2\).
А вот пример позабористее: \(\displaystyle {{0,1}^{x}}~>~0,01\).
Опять таки, легко сосчитать, что \(\displaystyle 0,01={{0,1}^{2}}\). И у нас получится \(\displaystyle {{0,1}^{x}}~>{{0,1}^{2}}\).
И какой можно из этого сделать вывод? Может быть, как и в предыдущем примере, \(\displaystyle x>2\)?
На первый взгляд, это кажется вполне очевидным. Но, увы, это не правильно.
Потому что, как ни парадоксально, из \(\displaystyle {{0,1}^{x}}~>{{0,1}^{2}}\) следует, что \(\displaystyle x<2\)!!
Неожиданно, правда?
Я бы мог долго распространяться, почему это так, умничая направо и налево, и бросаясь такими словами, как «монотонное возрастание» и «показательная функция», но я пожалею твое время и объясню простое правило.
Если основание в неравенстве больше \(\displaystyle 1\), то знак неравенства выполняется и для его показателей.
Если же основание больше \(\displaystyle 0\) и меньше \(\displaystyle 1\), то знак неравенства между его показателями меняется на противоположный.
Кратко это правило можно записать так:
\(\displaystyle {{a}^{x}}>{{a}^{y}}=>~x>y\) (при \(\displaystyle a>1\))
\(\displaystyle {{a}^{x}}>{{a}^{y}}=>~x<y\) (при \(\displaystyle 0<a<1\))
Такие же правила ты можешь получить для трех оставшихся знаков неравенств: \(\displaystyle <\),\(\displaystyle \le \),\(\displaystyle \ge \).
Я сказал «можешь»?
Нет, я ошибся: должен составить! Так тебе легче будет запомнить это нехитрое (самое нехитрое) правило.
Да, кстати, если ты внимательно читал мое изложение, то у тебя вполне могли появиться вопросы: а что если:
- Основание \(\displaystyle a=1\)?
- Основание \(\displaystyle a<0\)?
- Правая часть неравенства меньше нуля, например: \(\displaystyle {{2}^{x}}>-2\)?
Ответы вот:
- во-первых, не принято и не умеют решать показательные неравенства в которых \(\displaystyle a=1\) потому, что сколько единицу не умножай саму на себя (а именно это и делает степень), ничего кроме самой единицы ты все равно не получишь.
- То же самое касается и неравенств, в которых основание меньше нуля — просто забудь о них.
- Отдельного разговора (и абзаца) заслуживает последний случай.
Давай вместо основания возьмем число \(\displaystyle 2\) и будем возводить его во всевозможные степени:
| \(\displaystyle n\) | \(\displaystyle 0\) | \(\displaystyle 1\) | \(\displaystyle -1\) | \(\displaystyle 2\) | \(\displaystyle -2\) | \(\displaystyle 3\) | \(\displaystyle -3\) | \(\displaystyle 4\) | \(\displaystyle -4\) |
| \(\displaystyle {{2}^{n}}\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle \frac{1}{2}\) | \(\displaystyle 4\) | \(\displaystyle \frac{1}{4}\) | \(\displaystyle 8\) | \(\displaystyle \frac{1}{8}\) | \(\displaystyle 16\) | \(\displaystyle \frac{1}{16}\) |
Ты понял, как я заполнил эту таблицу? Нет!?
Стыд и позор, я же просил повторить свойства степени. Вернись и перечитай, а потом возвращайся к нам.
Итак, все стало понятно? Ну что же, продолжим.
Что мы видим в этой таблице?
Чем больше степень, тем больше значение выражения \(\displaystyle {{2}^{n}}\), и наоборот: чем меньше степень, тем это значение меньше.
Но, тем не менее, видно что, \(\displaystyle {{2}^{n}}\) всегда больше нуля.
ВСЕГДА. Это же свойство справедливо ДЛЯ ЛЮБОГО ОСНОВАНИЯ С ЛЮБЫМ ПОКАЗАТЕЛЕМ!!
\(\displaystyle {{a}^{x}}>0\) (для любых \(\displaystyle a\) и \(\displaystyle x\)).
Таким образом, уравнения вида \(\displaystyle {{a}^{x}}>0,{{a}^{x}}\ge 0\) имеют решения для любых \(\displaystyle x\) (это, как ты помнишь, записывается, \(\displaystyle x\in \left( -\infty ;+\infty \right)\)).
А вот неравенствам \(\displaystyle {{a}^{x}}<0,{{a}^{x}}\le 0\) повезло куда меньше: они не имеют решений.
Ну вот, все приличия соблюдены, теперь можно переходить уже к некоторым примерам:
- \(\displaystyle {{2}^{x}}<32\)
- \(\displaystyle {{4}^{x+2}}\le 64\)
- \(\displaystyle {{27}^{x+2}}\le 81\)
- \(\displaystyle {{\left( \frac{1}{3} \right)}^{2x}}>9\) (Правая часть неравенства меньше нуля \(\displaystyle {{2}^{x}}>-2\)?)
- \(\displaystyle {{\left( \frac{1}{5} \right)}^{-4x}}>\frac{1}{\sqrt{5}}\)
Решил? Честно? Ну хорошо, давай проверять вместе:
Пример 1. \(\displaystyle {{2}^{x}}<32,~{{2}^{x}}<{{2}^{5}}\), так как \(\displaystyle 2>1\), то \(\displaystyle x<5\).
Ответ, как ты помнишь, мы записываем следующим образом: \(\displaystyle x\in \left( -\infty ;5 \right)\).
Так как знак неравенства «строгий», то скобки будут «круглыми».
Пример 2. Здесь уже чуточку посложнее, но я уверен, ты тоже справился без проблем.
Сверяемся:
\(\displaystyle {{4}^{x+2}}\le 64\)
\(\displaystyle {{4}^{x+2}}\le {{4}^{3}}\)
так как \(\displaystyle 4>1\), то
\(\displaystyle x+2\le 3\), откуда \(\displaystyle x\le 1\),
Поэтому ответ:
\(\displaystyle x\in \left( -\infty ;1 \right]\).
Пример 3. \(\displaystyle {{27}^{x+2}}\le 81\).
Продолжаем нагромождать: в третьем примере нас ждет беда: так получилось, что \(\displaystyle 81\) это не целая степень числа \(\displaystyle 27\), (в чем несложно убедиться, возводя число \(\displaystyle 81\) в различные целые степени \(\displaystyle 0\), \(\displaystyle 1\), \(\displaystyle -1\)…).
И что же теперь делать? Бросать решение примера?
Нет! Этого не одобрю ни я, ни твой школьный учитель по математике.
Давай немного напряжемся и заметим, что и \(\displaystyle 27\) и \(\displaystyle 81\) это степени одного и того же числа. Какого? Конечно, это степени тройки (\(\displaystyle 27={{3}^{3}},~81={{3}^{4}}\)).
Тогда все становится сразу понятным:
\(\displaystyle {{27}^{x+2}}\le 81\)
\(\displaystyle {{3}^{3\left( x+2 \right)}}\le {{3}^{4}}\) (напомню, что при такой «замене» степени умножаются!).
Так как \(\displaystyle 3>1\), то знак неравенства не меняется и мы получаем:
\(\displaystyle 3\left( x+2 \right)\le 4\).
Раскроем скобки:
\(\displaystyle 3x+6\le 4,~3x\le -2,~x\le -\frac{2}{3}\).
Отсюда, ответ:
\(\displaystyle x\in \left( -\infty ;~-\frac{2}{3} \right]\).
Пример 4. Теперь мы решим еще более «навороченный» пример:
\(\displaystyle {{\left( \frac{1}{3} \right)}^{2x}}>9\)На самом деле, у нас есть аж два способа решить данное неравенство:
Во-первых, представить \(\displaystyle \frac{1}{3}\) как \(\displaystyle {{3}^{-1}}\)
(Если для тебя это «превращение» показалось магическим, перечитай свойства степени с отрицательным показателем)
Либо представить \(\displaystyle 9\) как \(\displaystyle {{\left( \frac{1}{3} \right)}^{-2}}\).
Мне хочется сейчас пойти именно вторым путем, ну а ты сам можешь применить первый. Как ты понимаешь, ответы должны совпасть.
\(\displaystyle {{\left( \frac{1}{3} \right)}^{2x}}>{{\left( \frac{1}{3} \right)}^{-2}}\)
Теперь слева и справа в неравенстве мы имеем одинаковые основания, значит мы можем перейти к неравенству относительно их показателей.
Однако, можно (и нужно!) заметить, что \(\displaystyle \frac{1}{3}<1\), поэтому знак неравенства меняется на противоположный.
Итого, мы получим: \(\displaystyle 2x<-2\),
Откуда простым делением на \(\displaystyle 2\) обеих частей неравенства очевидно следует, что \(\displaystyle x<-1\).
Записываем ответ: \(\displaystyle x\in \left( -\infty ;~-1 \right)\).
Пример 5. \(\displaystyle {{\left( \frac{1}{3} \right)}^{2x}}>9\)
Ну что же, здесь все нам тоже более-менее знакомо, единственно, что нужно вспомнить, так это то, что \(\displaystyle \frac{1}{\sqrt{5}}=\sqrt{\frac{1}{5}}={{\left( \frac{1}{5} \right)}^{\frac{1}{2}}}\).
Теперь окончательно получим:
\(\displaystyle {{\left( \frac{1}{5} \right)}^{-4x}}>{{\left( \frac{1}{5} \right)}^{\frac{1}{2}}}\).
Опять-таки \(\displaystyle \left( \frac{1}{5} \right)<1\), а значит знак неравенства меняется на противоположный:
\(\displaystyle -4x<\frac{1}{2}\).
Данное линейное неравенство решается делением левой и правой стороны на число, стоящее перед иксом: то есть делением на \(\displaystyle -4\).
Но мы ведь с тобой уже грамотные люди? Конечно! А потому мы помним, что при делении (или умножении) обеих частей неравенства на отрицательное число, знак неравенства МЕНЯЕТСЯ НА ПРОТИВОПОЛОЖНЫЙ.
А это значит, что
\(\displaystyle x>\frac{1}{2}:\left( -4 \right)\)
\(\displaystyle x>-\frac{1}{8}\)
Нам осталось лишь записать полученный правильный ответ:
\(\displaystyle x\in \left( -\frac{1}{8};~+\infty \right)\).
Задачки для совсем самостоятельного решения:
\(\displaystyle ~{{(\frac{1}{3})}^{({x} — 1)}}\le \frac{1}{9}\);
\(\displaystyle {{5}^{{x} — 1}}\le \sqrt{5}\);
\(\displaystyle {{7}^{{x} — 2}}>\sqrt[3]{49}\);
\(\displaystyle {{3}^{-2x}}<27\);
\(\displaystyle {{\left( \frac{1}{25} \right)}^{-2{x} — 4}}<{{625}^{-3x+5}}\).
А вот и ответы, заданные в измененном порядке, сверяйся!
\(\displaystyle \left( 2\frac{1}{3};~+\infty \right),~\left( -\infty ;~\frac{3}{4} \right),~\left[ 3;~+\infty \right),~\left[ 1\frac{1}{2};~+\infty \right),~\left( -1\frac{1}{2};~+\infty \right)\)
Нашел свои ответы в приведенном списке? Ничего лишнего и ничего не потерялось?
Прекрасно! Это значит, что теперь ты умеешь решать почти все показательные неравенства из первой части профильного ЕГЭ!
Но мы ведь с тобой хотим стать еще лучше и уметь решать еще более сложные неравенства?
Как ты без труда (или почти без труда) заметил, каждый раз, когда мы решали показательное неравенство, оно сводилось к некоторому линейному неравенству для показателей. Более того, каждая из частей (правая и левая) неравенства состояла ровно из одного выражения.
Что же запрещает природе вмешаться и сделать, например, с каждой стороны неравенства, скажем, не по одному выражению, а по три или даже четыре? Или же что ей запрещает составить такое неравенство, которое сводится уже не к линейному, а к квадратичному?
Правильно, ничего не запрещает. Поэтому мы должны быть готовы к решению и таких неравенств тоже. Давай вначале посмотрим на некоторые примеры:
\(\displaystyle {{5}^{{{x}^{2}}-5x+4}}>\frac{1}{25}\)
Применим к нему уже знакомую не понаслышке технику. Что же мы получим в итоге?
Верно:
\(\displaystyle {{x}^{2}}-5x+4>-2\).
Кто знает, что это такое? Конечно это квадратное неравенство! А теперь быстренько вспоминаем, как они решаются!
Да почти что как квадратные уравнения. А вот уж их ты точно умеешь решать, я не сомневаюсь.
\(\displaystyle {{x}^{2}}-5x+4=-2\),
\(\displaystyle {{x}^{2}}-5x+4+2=0\),
\(\displaystyle {{x}^{2}}-5x+6=0\).
Вычисляем дискриминант: \(\displaystyle D={{\left( -5 \right)}^{2}}-4\cdot 1\cdot 6=1\)
Так как дискриминант больше нуля, то уравнение имеет два корня:
\(\displaystyle {{x}_{1}}=\frac{-\left( -5 \right)+\sqrt{1}}{2\cdot 1}=3\), \(\displaystyle {{x}_{2}}=\frac{-\left( -5 \right)-\sqrt{1}}{2\cdot 1}=2\).
Если бы мы решали уравнение, то на этом можно было бы и остановиться. Но у нас с тобой более «высокая цель» – решение неравенства.
Поэтому далее нам нужен метод интервалов.
Метод интервалов
Метод интервалов — самый универсальный способ решения неравенств. Но он особенно эффективен при решении квадратных неравенств.
В этом разделе разберем алгоритм решения квадратных неравенств с помощью метода интервалов. И конечно же решим пару-тройку примеров.
Поехали!
Отметим эти точки на координатной прямой и разделим эту прямую на три интервала, затем выберем какое-нибудь число в любом из интервалов и вычислим, чему равно наше исходное выражение \(\displaystyle {{x}^{2}}-5x+6\) в этой точке.
Мне нравится брать такое число, чтобы нужно было как можно меньше считать. Догадался, какое же это число? Верно, это ноль.
Ноль принадлежит самому левому интервалу.
Наше выражение, если подставить в него ноль вместо икса, будет равно \(\displaystyle 6\), \(\displaystyle 6>0\).
Поэтому в левом интервале я ставлю знак \(\displaystyle +\). Далее чередую.
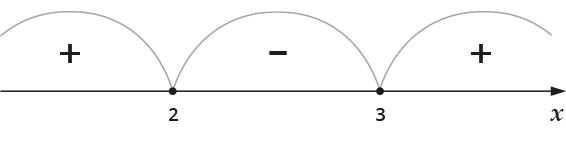
Поскольку мы решаем неравенство \(\displaystyle {{x}^{2}}-5x+6>0\), то нас интересуют те промежутки, где это выражение положительно (то есть стоит \(\displaystyle +\)).
Таким образом, наш ответ будет:
\(\displaystyle x\in \left( -\infty ;2 \right)\mathop{\cup }^{}\left( 3;+\infty \right)\).
Теперь мне кажется, что ты без особого труда решишь следующие примеры:
\(\displaystyle {{\left( \frac{13}{11} \right)}^{{{x}^{2}}-3x}}<\frac{121}{169}\);
\(\displaystyle {{2}^{{{x}^{2}}}}>{{\left( \frac{1}{2} \right)}^{2{x} — 3}}\).
Давай сверяться вместе:
Пример 1. \(\displaystyle {{\left( \frac{13}{11} \right)}^{{{x}^{2}}-3x}}<\frac{121}{169}\);
\(\displaystyle {{\left( \frac{13}{11} \right)}^{{{x}^{2}}-3x}}<{{\left( \frac{11}{13} \right)}^{2}}\);
\(\displaystyle \text{ }\!\!~\!\!\text{ }{{\left( \frac{13}{11} \right)}^{{{x}^{2}}-3x}}<{{\left( \frac{13}{11} \right)}^{-2}}\)
Так как \(\displaystyle \frac{13}{11}>1\), то \(\displaystyle {{x}^{2}}-3x<-2\)
Пример 2. Второе неравенство тоже решается элементарно, давай проверим:
\(\displaystyle {{2}^{{{x}^{2}}}}>{{\left( \frac{1}{2} \right)}^{2{x} — 3}}\)
\(\displaystyle {{2}^{{{x}^{2}}}}>{{\left( {{2}^{-1}} \right)}^{2{x} — 3}}\)
\(\displaystyle {{2}^{{{x}^{2}}}}>{{2}^{-\left( 2{x} — 3 \right)}}\).
Откуда \(\displaystyle {{x}^{2}}>-\left( 2{x} — 3 \right)\).
Что эквивалентно следующему квадратному неравенству:
Как видишь, решение подобных примеров чуть сложнее, чем тех, которые мы решали в самом начале.
Но тем не менее здесь нам уже требуется использовать такой мощный метод, как МЕТОД ИНТЕРВАЛОВ.
Вообще говоря, большинство неравенств именно с его помощью и решается. Так что можно сказать, что в начале нам просто «везло» и мы обходились без него.
Метод группировки
Впервые ты столкнулся с методом группировки в 7 классе, когда раскладывал сложные выражения на простые множители, например:
\(\displaystyle 3ab+{{b}^{2}}+6{{a}^{3}}+2{{a}^{2}}b=b\left( 3a+b \right)+2{{a}^{2}}\left( 3a+b \right)=\left( b+2{{a}^{2}} \right)\left( 3a+b \right)\)
Как ни парадоксально, но что-то подобное может применяться и при решении таких монстров как показательные неравенства.
Да и что сказать, их используют, чтобы справиться с такими чудовищами, по сравнению с которыми наши неравенства покажутся белыми и пушистыми.
Но перейдем от слов к делу.
Допустим, нам требуется решить следующее неравенство:
\(\displaystyle {{3}^{x+2}}+{{3}^{{x} — 1}}<28\)
Согласись, до этих пор мы ни с чем подобным не сталкивались. Однако не время унывать. Давай подумаем, что общего есть у слагаемых слева?
Верно, все они – это тройка в некоторой степени. Со свойствами степени мы уже давно на «ты», я ведь прав? Отлично!
Тогда давай вынесем, например \(\displaystyle {{3}^{x}}\) из каждого выражения. Что мы получим?
\(\displaystyle {{3}^{x}}{{3}^{2}}+{{3}^{x}}{{3}^{-1}}<28\)
Эврика! У нас есть общий множитель! Так чего же мы ждем? Срочно выносим его за скобки!
\(\displaystyle {{3}^{x}}({{3}^{2}}+{{3}^{-1}})<28\)
Теперь вычисляем значение выражения внутри скобок:
\(\displaystyle {{3}^{2}}+{{3}^{-1}}=9+\frac{1}{3}=\frac{9\cdot 3+1}{3}=\frac{28}{3}\);
Ну теперь осталась самая малость: подставим полученное выражение в наше неравенство:
Давай решим следующее неравенство, но теперь я буду менее многословен, так что тебе придется многое додумывать самому:
\(\displaystyle 8\cdot {{2}^{{x} — 1}}-{{2}^{x}}>48\)
Вынесем за скобку множитель \(\displaystyle {{2}^{{x} — 1}}\):
Предварительные выводы
Разумеется, описанные в данной статье методы решений показательных неравенств далеко не исчерпывают весь спектр методов, которые применяются при решении такого вида неравенств.
Да и сами неравенства далеко не всегда легки и понятны. Более того, к некоторым неравенствам даже математик не всегда сразу знает, «как подступиться».
Неравенства бывают самыми разнообразными. Насколько хватит твоего полета фантазии. Здесь же я описал подход к решению самых простейших.
Надеюсь, прочтение этих разделов было для тебя если не полезным, то по крайней мере не утомительным. Желаю тебе не останавливаться на достигнутом и двигаться дальше! Навстречу новым рубежам!
Ну а пока несколько примеров на повторение пройденного материала!
Показательные неравенства — повторение пройденного (решение 10 неравенств)
Пример 1. \({{\left( 0,3 \right)}^{\frac{x}{{x} — 2}}}<{{\left( 0,3 \right)}^{\frac{6}{{x} — 1}}}\);
Пример 2. \({{0,1}^{2{{x}^{2}}-3x+6}}<0,0001\);
Пример 3. \({{3}^{\frac{2{x} — 1}{{x} — 2}}}<1\);
Пример 4. \({{5}^{4x+2}}<\frac{125}{\sqrt{{{5}^{-6}}}}\);
Пример 5. \(\displaystyle {{\left( \frac{2}{7} \right)}^{3\left( 2{x} — 7 \right)}}{{\left( \frac{49}{4} \right)}^{2x+0,5}}\ge 1\);
Пример 6. \({{\sqrt{7}}^{{x} — 1}}>\frac{1}{{{49}^{x}}}\);
Пример 7. \({{0,4}^{2{x} — 1}}\le {{0,16}^{3x+2}}\);
Пример 8. \({{2}^{3-x}}+{{2}^{1-x}}>40\);
Пример 9. \({{3}^{x+2}}+{{3}^{x+1}}+{{3}^{x}}\le 39\);
Пример 10. \({{2}^{3}}{{2}^{x+5}}>16\).
Решения:

Пример 1. \({{\left( 0,3 \right)}^{\frac{x}{{x} — 2}}}<{{\left( 0,3 \right)}^{\frac{6}{{x} — 1}}}\), т.к. \(0,3<1\), то \(\frac{x}{{x} — 2}>\frac{6}{{x} — 1}\)
Приведем дроби к общему знаменателю:
\(\frac{x\left( {x} — 1 \right)}{\left( {x} — 2 \right)\left( {x} — 1 \right)}>\frac{6\left( {x} — 2 \right)}{\left( {x} — 2 \right)\left( {x} — 1 \right)},~\frac{x\left( {x} — 1 \right)-6\left( {x} — 2 \right)}{\left( {x} — 2 \right)\left( {x} — 1 \right)}>0\),
\(\frac{{{x}^{2}}-{x} — 6x+12}{\left( {x} — 2 \right)\left( {x} — 1 \right)}>0,~\frac{{{x}^{2}}-7x+12}{\left( {x} — 2 \right)\left( {x} — 1 \right)}>0\)
Разложим \({{x}^{2}}-7x+12\) на множители:
Пример 2. \({{0,1}^{2{{x}^{2}}-3x+6}}<0,0001\)
Тогда
\({{0,1}^{2{{x}^{2}}-3x+6}}<{{0,1}^{4}}\)
Значит
\(2{{x}^{2}}-3x+6>4\),
\(2{{x}^{2}}-3x+2>0\).
Дискриминант уравнения \(2{{x}^{2}}-3x+2=0\) равен \(D={{\left( -3 \right)}^{2}}-4\cdot 2\cdot 2=-7<0\)
Значит, уравнение не имеет корней.
Пример 3. \({{3}^{\frac{2{x} — 1}{{x} — 2}}}<1\)
Тогда
\(\frac{2{x} — 1}{{x} — 2}<0\) данное неравенство снова решается методом интервалов.
Нанесем корни числителя и знаменателя на координатную ось, расставим знаки и получим ответ:
Пример 4. \({{5}^{4x+2}}<\frac{125}{\sqrt{{{5}^{-6}}}}\)
Преобразуем выражение справа:
\(\frac{125}{\sqrt{{{5}^{-6}}}}=\frac{{{5}^{3}}}{{{5}^{\frac{-6}{2}}}}=\frac{{{5}^{3}}}{{{5}^{-3}}}={{5}^{3-\left( -3 \right)}}={{5}^{6}}\)
Подставим полученное выражение в правую часть неравенства:
Пример 5. \({{\left( \frac{2}{7} \right)}^{3\left( 2{x} — 7 \right)}}{{\left( \frac{49}{4} \right)}^{2x+0,5}}\ge 1\),
\({{\left( \frac{2}{7} \right)}^{3\left( 2{x} — 7 \right)}}{{\left( \frac{{{7}^{2}}}{{{2}^{2}}} \right)}^{2x+0,5}}\ge 1\),
\({{\left( \frac{2}{7} \right)}^{3\left( 2{x} — 7 \right)}}{{\left( \frac{7}{2} \right)}^{2\left( 2x+0,5 \right)}}\ge 1\),
так как \({{\left( \frac{2}{7} \right)}^{-1}}=\frac{7}{2}\), то
Пример 6. \({{\sqrt{7}}^{{x} — 1}}>\frac{1}{{{49}^{x}}}\),
так как \(\sqrt{7}={{7}^{0,5}}\), а \(\frac{1}{{{49}^{x}}}={{\left( \frac{1}{49} \right)}^{x}}={{\left( \frac{1}{7} \right)}^{2x}}={{7}^{-2x}}\), то
\({{7}^{0,5\left( {x} — 1 \right)}}>{{7}^{-2x}}\), что эквивалентно:
Пример 7. \({{0,4}^{2{x} — 1}}\le {{0,16}^{3x+2}}\), откуда
\({{0,4}^{2{x} — 1}}\le {{0,4}^{2\left( 3x+2 \right)}}\),
так как \(0,4<1\), то
Пример 8. \({{2}^{3-x}}+{{2}^{1-x}}>40\),
\({{2}^{-x}}\left( {{2}^{3}}+2 \right)>40\),
\({{2}^{-x}}>4\),
\(-x>2,~x<-2\)
Ответ: \(x\in \left( -\infty ;~-2 \right)\).
Пример 9. \({{3}^{x+2}}+{{3}^{x+1}}+{{3}^{x}}\le 39\),
\({{3}^{x}}\left( {{3}^{2}}+3+1 \right)\le 39\),
\({{3}^{x}}\cdot 13\le 39\),
\({{3}^{x}}\le 3\), откуда \({{3}^{x}}\le 3\).
Ответ: \(x\in \left( -\infty ;1 \right]\)
Пример 10. \({{2}^{3}}{{2}^{x+5}}>16\),
\({{2}^{x+8}}>{{2}^{4}}\),
\(x+8>4,~x>-4\).
Ответ: \(x\in \left( -4;~+\infty \right)\).
Подведем итоги
Методы решения показательных неравенств во многом дублируют способы решения показательных уравнений.
Вот только что мы ищем при решении уравнения? Верно, корни соответствующего уравнения. Или же показываем, что их нет.
В неравенстве мы будем искать промежутки (то есть те множества значений переменной, на которой данное неравенство выполняется).
Для этого используют различные методы.
Вспомни, к чему сводилось решение показательного уравнения? Да, мы сводили его к такому виду:
\({{a}^{f\left( x \right)}}={{a}^{g\left( x \right)}}\)
После чего делали вывод, что \(f\left( x \right)=g\left( x \right)\) и решали уже полученное уравнение. Практически аналогичным образом мы поступаем и с показательным неравенством.
Определение:
Простейшими показательными неравенствами являются неравенства следующего вида:
\({{a}^{f\left( x \right)}}>{{a}^{g\left( x \right)}},~{{a}^{f\left( x \right)}}<{{a}^{g\left( x \right)}},~{{a}^{f\left( x \right)}}\ge {{a}^{g\left( x \right)}},~{{a}^{f\left( x \right)}}\le {{a}^{g\left( x \right)}}\),
где \(a\) – основание, \(f\left( x \right),~g\left( x \right)\) – показатели.
Например, в неравенстве \({{3}^{3\left( x+2 \right)}}\le {{3}^{4}}\) \(a=3\) – основание, \(f\left( x \right)=3\left( x+2 \right)\), \(g\left( x \right)=4\) – показатели.
Существует основное правило решения показательных неравенств.
Обрати на него особое внимание. Незнание этого правила является очень частой причиной глупейших (и оттого еще более обидных ошибок).
| Правило:\({{a}^{f\left( x \right)}}>{{a}^{g\left( x \right)}}=>~f\left( x \right)>g\left( x \right)\) \(\left(\text{при} ~a>1 \right)\) \({{a}^{f\left( x \right)}}>{{a}^{g\left( x \right)}}=>~f\left( x \right)<g\left( x \right)\) \(\left(~0<a<1 \right)\) |
Аналогичные законы справедливы и для трех оставшихся знаков неравенств.
Сформулируй правила самостоятельно.
Теперь перейдем к методам решения показательных неравенств. Я могу выделить 5 методов их решения.
5 методов решения показательных неравенств
- Метод №1. Преобразование оснований
- Метод №2. Разложение на множители
- Метод №3. Замена переменной
- Метод №4 Метод декомпозиции
- Метод №5. Анализ монотонности функций
Первые три метода относительно простые, а последние два… да тоже простые ).
Метод декомпозиции поможет разобраться с показательными неравенствами с переменным основанием.
А анализ монотонности функций — со смешанными неравенствами, которые никак иначе не решаются.
Начнем?
Метод №1. Преобразование оснований
Если неравенство имеет вид: \({{a}^{f\left( x \right)}}>{{b}^{g\left( x \right)}}\), то работаем с основаниями.
Преобразовываем их к такому виду, чтобы они являлись степенями одного и того же числа. \(a={{c}^{q}},~b={{c}^{t}}\), а затем решаем простейшее неравенство \({{с}^{qf\left( x \right)}}>{{c}^{tg\left( x \right)}}\).
Кажется немного непонятно, не так ли? Однако дай мне пару минут, и все встанет на свои места. Реши следующие неравенства.
Пример 1. \({{27}^{x+2}}\le 81\)
Решение:
Заметим, что \(27={{3}^{3}},~81={{3}^{4}}\). Таким образом, левая и правая часть неравенства – есть степени тройки. Тогда все становится сразу понятным: исходное неравенство равносильно такому: \({{3}^{3\left( x+2 \right)}}\le {{3}^{4}}\), так как \(3>1\), то получаем, что \(3\left( x+2 \right)\le 4\), раскроем скобки:
\(3x+6\le 4,~3x\le -2,~x\le -\frac{2}{3}\).
Отсюда, ответ: \(x\in \left( -\infty ;~-\frac{2}{3} \right]\).
Теперь еще один пример, немного посложнее.
Пример 2. \({{5}^{4x+2}}<\frac{125}{\sqrt{{{5}^{-6}}}}\)
Ну и для закрепления последний пример на первый метод решения.
Пример 3. \({{2}^{{{x}^{2}}}}>{{\left( \frac{1}{2} \right)}^{2{x} -3}}\)
Решение:
\({{2}^{{{x}^{2}}}}>{{\left( {{2}^{-1}} \right)}^{2{x} -3}}\),
\({{2}^{{{x}^{2}}}}>{{2}^{-\left( 2{x} -3 \right)}}\), откуда
\({{x}^{2}}>-\left( 2{x} -3 \right)\), что эквивалентно следующему квадратному неравенству:
Метод №2. Разложение на множители
Вторым методом решения неравенств является хорошо тебе знакомое разложение на множители.
Много слов не нужно. Просто решай примеры.
Пример 1. \({{3}^{x+2}}+{{3}^{{x} -1}}<28\)
Решение:
Вынесем общий множитель в выражении слева за скобки. Какое выражение является этим множителем?
Конечно же, это \({{3}^{{x} -1}}\)
Тут стоит не кривить душой и сказать, что вы бы могли вынести и просто \({{3}^{x}}\), и результат бы совпал, но принято выносить за скобки наименьшую из возможных степеней.
Итого, получим:
\({{3}^{{x} -1}}({{3}^{3}}+{{3}^{1}})<28\),
\({{3}^{{x} -1}}\cdot 28<28\),
\({{3}^{{x} -1}}<1={{3}^{0}}\),
\(x<1\).
Ответ: \(x\in \left( -\infty ;1 \right)\).
Ничего сложного, правда? Все почти как в 7 классе, с той лишь разницей, что тут объекты немного другие.
Пример 2. \({{3}^{x+2}}+{{3}^{x+1}}+{{3}^{x}}\le 39\)
Решение:
\({{3}^{x}}\left( {{3}^{2}}+3+1 \right)\le 39\),
\({{3}^{x}}\cdot 13\le 39\),
\({{3}^{x}}\le 3\),
откуда \(x\le 1\).
Ответ: \(x\in \left( -\infty ;1 \right]\).
Пример 3. \({{\left( 0,3 \right)}^{\frac{x}{{x} -2}}}<{{\left( 0,3 \right)}^{\frac{6}{{x} -1}}}\)
\({{\left( 0,3 \right)}^{\frac{x}{{x} -2}}}<{{\left( 0,3 \right)}^{\frac{6}{{x} -1}}}\), т.к. \(0,3<1\), то
\(\frac{x}{{x} -2}>\frac{6}{{x} -1}\),
приведем дроби к общему знаменателю:
Пример 4. \({{3}^{\frac{2{x} -1}{{x} -2}}}<1\)
\({{3}^{\frac{2{x} -1}{{x} -2}}}<1\), тогда \(\frac{2{x} -1}{{x} -2}<0\).
Данное неравенство снова решается методом интервалов:
Нанесем корни числителя и знаменателя на координатную ось, расставим знаки и получим ответ: \(x\in \left( \frac{1}{2};2 \right)\)
Пример 5. \({{\left( \frac{2}{7} \right)}^{3\left( 2{x} -7 \right)}}{{\left( \frac{49}{4} \right)}^{2x+0,5}}\ge 1\)
\({{\left( \frac{2}{7} \right)}^{3\left( 2{x} -7 \right)}}{{\left( \frac{49}{4} \right)}^{2x+0,5}}\ge 1\),
\({{\left( \frac{2}{7} \right)}^{3\left( 2{x} -7 \right)}}{{\left( \frac{{{7}^{2}}}{{{2}^{2}}} \right)}^{2x+0,5}}\ge 1\),
\({{\left( \frac{2}{7} \right)}^{3\left( 2{x} -7 \right)}}{{\left( \frac{7}{2} \right)}^{2\left( 2x+0,5 \right)}}\ge 1\),
так как \({{\left( \frac{2}{7} \right)}^{-1}}=\frac{7}{2}\), то
Пример 6. \({{2}^{3-x}}+{{2}^{1-x}}>40\)
\({{2}^{-x}}\left( {{2}^{3}}+2 \right)>40\),
\({{2}^{-x}}>4\),
\(-x>2,~x<-2\)Ответ: \(x\in \left( -\infty ;~-2 \right)\).
Пример 7. \({{\left( \frac{13}{11} \right)}^{{{x}^{2}}-3x}}<\frac{121}{169}\)
\({{\left( \frac{13}{11} \right)}^{{{x}^{2}}-3x}}<\frac{121}{169}\),
\({{\left( \frac{13}{11} \right)}^{{{x}^{2}}-3x}}<{{\left( \frac{11}{13} \right)}^{2}}\),
\({{\left( \frac{13}{11} \right)}^{{{x}^{2}}-3x}}<{{\left( \frac{13}{11} \right)}^{-2}}\), так как \(\frac{13}{11}>1\), то
Метод №3. Замена переменной
Еще одним приемом является замена переменной.
В таком случае мы сразу же сводим показательное неравенство к более простому виду: например, к квадратичному.
Затем решаем это «простое» неравенство и делаем обратную замену.
Вспомни, например, как решается уравнение
\({{x}^{4}}+{{x}^{2}}-6=0\),
Вспомнил?
Ты делал простую замену \(t={{x}^{2}}\), не забывая, что \(t\ge 0\), а затем уже решал совсем простое уравнение \({{t}^{2}}+t-6=0\), находил его корни \({{t}_{1}}=-3\) (этот корень нам не подходит, так как он меньше нуля), \({{t}_{2}}=2\), а затем делал обратную замену: \(2={{x}^{2}}\)
Последнее уравнение имеет корни \({{x}_{1}}=\sqrt{2},~{{x}_{2}}=-\sqrt{2}\), которые и являются корнями нашего исходного уравнения.
При решении неравенств мы тоже можем прибегнуть к приему замены переменной. Но здесь есть один подводный камень… Заинтригован? Тогда решаем вместе!
Пример 1. \(3\cdot {{5}^{x}}-5\cdot {{25}^{x}}+2>0\)
Решение:
Перепишем данное неравенство в следующем виде:
\(3\cdot {{5}^{x}}-5\cdot {{5}^{2x}}+2>0\)
Теперь пора задуматься, а что дальше? Ясно, что первый метод решения здесь не поможет: у нас есть «противная» двойка, от которой нам никак не избавиться.
Это же мешает применить разложение на множители: от двойки мы никак не избавимся. Да и вынести выражение так, чтобы только одно выражение содержало \(x\), также не получится.
Надо придумать замену.
Какую? Обычно принято заменять выражение, содержащее минимальную степень \(x\).
В нашем случае это \({{5}^{x}}\). Если мы введем замену \(t={{5}^{x}}\), то чем же будет являться \({{25}^{x}}={{5}^{2x}}\)?
Да, ты абсолютно правильно понял, \({{5}^{2x}}={{t}^{2}}\). Тогда исходное выражение будет равносильно следующему:
\(3\cdot t-5\cdot {{t}^{2}}+2>0\)
Решим данное неравенство, предварительно умножив его на \(\left( -1 \right)\):
\(5\cdot {{t}^{2}}-3\cdot t-2<0\)
Решениями соответствующего уравнения будут числа:
\({{t}_{1}}=1,~{{t}_{2}}=-\frac{2}{5}\).
Нас интересует знак «\(—\)«, поэтому решениями соответствующего неравенства будет промежуток \(-\frac{2}{5}<t<1\). (конечный !!!!)
Данное двойное неравенство равносильно системе:
\(\left\{ \begin{array}{l}t>-\frac{2}{5}\\t<1\end{array} \right.\).
Теперь вспомним о том, что такое \(t\): \(t={{5}^{x}}\). Тогда получим систему уже относительно \(x\):
\(\displaystyle \left( 1 \right)\ \ \left\{ \begin{array}{l}{{5}^{x}}>-\frac{2}{5}\\{{5}^{x}}<1\end{array} \right.\)
Известен факт, что выражение
\({{a}^{x}}>0\) (для любых \(a\) и \(x\)).
Таким образом, что можно сказать про наше первое неравенство в системе?
Да! Нам несказанно повезло, оно имеет решения при всех \(x\)!!!!
Так что решение системы будет равносильно решению второго ее неравенства! Здорово, правда?
Теперь разберемся со вторым неравенством.
Пример 2. \(\displaystyle 4\cdot {{4}^{x}}-29\cdot {{10}^{x}}+25\cdot {{25}^{x}}\le 0\)
Решение:
Здесь мы столкнулись с тем, что сделать замену напрямую не представляется возможным – четверка – это степень двойки, а \(\displaystyle 25\) – степень пятерки.
Однако у нас есть еще одно слагаемое посередине – \(\displaystyle {{10}^{x}}\), которое равно \(\displaystyle {{5}^{x}}{{2}^{x}}\).
Также представим \(\displaystyle {{4}^{x}}={{2}^{2x}},~{{25}^{x}}={{5}^{2x}}\):
\(\displaystyle 4\cdot {{2}^{2x}}-29\cdot {{5}^{x}}{{2}^{x}}+25\cdot {{5}^{2x}}\le 0\)
Теперь у нас есть одно слагаемое, содержащее степень двойки, одно – степень пятерки, и еще одно посередине – содержит произведение степеней.
Прием, который позволяет решать такие неравенства заключается в делении обеих его частей на либо \(\displaystyle {{2}^{2x}}\) либо \(\displaystyle {{5}^{2x}}\).
Что же у нас получится? Я разделю на \(\displaystyle {{5}^{2x}}\):
\(\displaystyle 4\cdot \frac{{{2}^{2x}}}{{{5}^{2x}}}-29\cdot \frac{{{5}^{x}}{{2}^{x}}}{{{5}^{2x}}}+25\le 0\)
Преобразую, используя свойства степеней:
\(\displaystyle 4\cdot {{\left( \frac{2}{5} \right)}^{2x}}-29\cdot {{\left( \frac{2}{5} \right)}^{x}}+25\le 0\)
Теперь замена очевидна, правда?
\(\displaystyle 4\cdot {{t}^{2}}-29\cdot t+25\le 0\), где \(\displaystyle t={{\left( \frac{2}{5} \right)}^{x}}\)
Решаю последнее неравенство, получу (а ты получи сам!!) систему:
Не так уж все и страшно, правда?
Пример 3. \(\displaystyle \sqrt{{{9}^{x}}-{{3}^{x+2}}}>{{3}^{x}}-9\)
\(\displaystyle \sqrt{{{9}^{x}}-{{3}^{x+2}}}>{{3}^{x}}-9\Rightarrow \) \(\displaystyle \sqrt{{{3}^{2x}}-9\cdot {{3}^{x}}}>{{3}^{x}}-9,\ t={{3}^{x}}\Rightarrow \)\(\displaystyle \sqrt{{{t}^{2}}-9\cdot t}>t-9\), откуда:
\(\displaystyle \left\{ \begin{array}{l}{{t}^{2}}-9t\ge 0~\left( ОДЗ\ квадратного\ корня \right)\\t>0~\left( из-за\ замены \right)\\{{t}^{2}}-9\cdot t>{{\left( t-9 \right)}^{2}}\end{array} \right.\)Решение полученной системы, а так же обратную замену я предоставляю тебе в качестве упражнения.
Ответ: \(\left(2; +\infty \right)\).
Пример 4. \(\displaystyle 3\cdot {{2}^{2x}}-5\cdot {{6}^{x}}+2\cdot {{3}^{2x}}>0\)
Делим обе части на \(\displaystyle {{3}^{2x}}\), получим:
\(\displaystyle 3{{\left( \frac{2}{3} \right)}^{2x}}-5{{\left( \frac{2}{3} \right)}^{x}}+2>0\),
замена \(\displaystyle t={{\left( \frac{2}{3} \right)}^{x}}\) приводит к неравенству:
\(\displaystyle 3{{t}^{2}}-5t+2>0\),
Которое я опять-таки доверяю решить тебе самостоятельно. Уверен, ты меня не подведешь!
Ответ: \(\displaystyle x\in \left( -\infty ;0 \right)\mathop{\cup }^{}\left( 1;+\infty \right)\)
Пример 5. \(\displaystyle {{\left( \frac{1}{36} \right)}^{x}}-5\cdot {{6}^{-x}}-6<0\)
\(\displaystyle {{\left( \frac{1}{36} \right)}^{x}}-5\cdot {{6}^{-x}}-6<0\),
сделаем замену \(\displaystyle t={{6}^{-x}}\), получим:
\(\displaystyle {{t}^{2}}-5t-6<0\) и т. д.
Ответ: \(\displaystyle x\in \left( -1;+\infty \right)\)
Пример 6. \(\displaystyle {{2}^{x+2}}-{{2}^{x+3}}-{{2}^{x+4}}>{{5}^{x+1}}+{{5}^{x+2}}\)
Вынесем общий множитель из левой и правой части:
\(\displaystyle {{2}^{x}}\left( 4-8-16 \right)>{{5}^{x}}\left( 5+25 \right)\)Левая часть неравенства всегда меньше нуля, а правая – всегда больше, значит, левая часть никогда не превосходит правую, и неравенство не имеет решений.
Пример 7. \(\displaystyle {{6}^{\frac{{x} -7}{3}}}-{{6}^{\frac{13-x}{3}}}-35>0\)
\(\displaystyle {{6}^{\frac{{x} -7}{3}}}-{{6}^{\frac{13-x}{3}}}-35>0\Rightarrow \) \(\displaystyle \Rightarrow {{6}^{\frac{x}{3}}}{{6}^{\frac{-7}{3}}}-{{6}^{-\frac{x}{3}}}{{6}^{\frac{13}{3}}}-35>0,\)\(\displaystyle {{6}^{\frac{x}{3}}}{{6}^{\frac{-7}{3}}}-\frac{1}{{{6}^{\frac{x}{3}}}}{{6}^{\frac{13}{3}}}-35>0\),
замена \(\displaystyle t={{6}^{\frac{x}{3}}}\) и умножение обеих частей неравенства на \(\displaystyle t\) приводит к неравенству
\(\displaystyle {{6}^{\frac{-7}{3}}}{{t}^{2}}-{{6}^{\frac{13}{3}}}-35t>0\), решение которого остается на твоей совести.
Ответ: \(\displaystyle x\in \left(13;+\infty \right)\).
Теперь мы с тобой владеем всеми необходимыми знаниями для решения таких неподступных «монстров», как неравенства повышенной сложности из ЕГЭ.
Конечно, те неравенства в которых есть пока что «непонятные» логарифмы, я здесь не привожу (приведу далее, так что от них ты тоже никуда не денешься), а вот с показательными мы вполне в состоянии справиться!
Здесь нет ничего сложного, вся техника для их решения уже у тебя в руках!
Давай посмотрим еще на один совсем простой пример (ума не приложу, почему он считается сложным?!)
Пример 8. \(\displaystyle \left\{ \begin{array}{l}{{5}^{x}}+{{\left( \frac{1}{5} \right)}^{x}}>2\\{{2}^{{{x}^{2}}}}\le 64\cdot {{2}^{x}}\end{array} \right.\)
Решение:
Не так страшен черт, как его малюют 🙂 Берем первое неравенство:
\(\displaystyle {{5}^{x}}+{{\left( \frac{1}{5} \right)}^{x}}>2\).
Перепишем его в виде: \(\displaystyle {{5}^{x}}+{{5}^{-x}}>2\) и домножим обе части на положительное выражение \(\displaystyle {{5}^{x}}\), тогда получим:
\(\displaystyle {{5}^{2x}}+1-2\cdot {{5}^{x}}>0\).
Я думаю, ты догадался, что дальше)
Пример 9. Вверху у нас – показательное неравенство, а снизу – дробно-рациональное:
\(\displaystyle \left\{ \begin{array}{l}\frac{2}{{{5}^{x}}-1}+\frac{{{5}^{x}}-2}{{{5}^{x}}-3}\ge 2\\{{\left( \frac{2}{25{{x}^{2}}-10{x} -8}+\frac{25{{x}^{2}}-10{x} -8}{2} \right)}^{2}}\ge 4\end{array} \right.\)
Очередная помесь «бульдога с носорогом». Вверху у нас – показательное неравенство, а снизу – дробно-рациональное, причем устрашающего вида.
Вот с него бы мне и хотелось начать.
Решение:
Конечно, ничто не мешает нам решить его, как говорится, в «лоб». Только сам его вид должен отталкивать тебя от такой неразумной мысли. Все на самом деле довольно просто.
Давай заметим, что первое слагаемое скобки – перевернутое второе и наоборот. Таким образом, я могу сказать, что внутри у нас написана сумма величин вида: \(\displaystyle a+\frac{1}{a}\).
Знаешь, как называются такие величины? Они называются взаимно-обратными.
Кстати, посмотри на первое уравнение предыдущего примера. Увидел? Да, там тоже сумма подобного вида. В том случае мы доказали, что неравенству удовлетворяют все действительные числа, кроме нуля. При нуле мы получали двойку.
Таким образом, я утверждаю, что для всех сумм вида: \(\displaystyle a+\frac{1}{a}\) выполняется следующее неравенство:
\(\displaystyle a+\frac{1}{a}\ge 2\), при \(\displaystyle a>0\);
\(\displaystyle a+\frac{1}{a}\le -2\), при \(\displaystyle a<0\).
Ты можешь сам без труда доказать это утверждение. А что же из него следует? А вот что:
\(\displaystyle {{\left( a+\frac{1}{a} \right)}^{2}}\ge 4\), при всех \(\displaystyle a\ne 0\)!!!
Таким образом, нам лишь нужно «откинуть» те значения, при которых выражение \(\displaystyle 25{{x}^{2}}-10{x} -8\) равно нулю (иначе оно обнулит знаменатель!).
Мы без труда найдем такие числа:
\(\displaystyle {{x}_{1}}=\frac{4}{5},{{x}_{2}}=-\frac{2}{5}\).
Тогда второе неравенство имеет место при всех действительных \(\displaystyle x\), кроме \(\displaystyle \frac{4}{5}\), \(\displaystyle -\frac{2}{5}\).
Теперь решим первое неравенство: \(\displaystyle \frac{2}{{{5}^{x}}-1}+\frac{{{5}^{x}}-2}{{{5}^{x}}-3}\ge 2\).
Сразу же сделаем замену переменных: \(\displaystyle t={{5}^{x}}\). Тогда получим:
\(\displaystyle \frac{2}{t-1}+\frac{t-2}{t-3}\ge 2\)
Приведем выражение к общему знаменателю и получим:
\(\displaystyle \frac{\left( t-5 \right)\left( t-2 \right)}{\left( t-1 \right)\left( t-3 \right)}\le 0\)
Решим данное неравенство методом интервалов, тогда получим:
Метод №4. Метод декомпозиции при решении показательных неравенств
В заключение я бы хотел рассмотреть еще один мощный метод решения показательных неравенств – метод декомпозиции.
Он особенно тебе пригодится, когда тебе придется иметь дело с показательными неравенствами с переменным основанием. Например, с вот таким:
\(\displaystyle {{\left| {x} -3 \right|}^{\frac{{{x}^{2}}-8x+15}{{x} -2}}}>1\)
В чем вся беда? А неприятность в том, что переменная в основании влияет на знак неравенства между показателями.
В самом деле, если основание больше единицы, то знак неравенства сохраняется, а если же оно больше нуля и меньше единицы, то знак неравенства меняется на противоположный.
Однако, существует универсальный метод решения таких сложных неравенств. Это метод декомпозиции, сводящий одно сложное неравенство к куче мелких, но попроще.
Вначале я рассмотрю формулы, а потом применю их к нашему примеру.
Неравенство \(\displaystyle h{{\left( x \right)}^{g\left( x \right)}}~\vee ~h{{\left( x \right)}^{f\left( x \right)}}~\left( 1 \right)\) равносильно следующей системе: \(\displaystyle \left\{ \begin{array}{l}\left( h\left( x \right)-1 \right)\left( g\left( x \right)-f\left( x \right) \right)\ \vee ~0\\h\left( x \right)>0\end{array} \right.\)
Неравенство \(\displaystyle h{{\left( x \right)}^{g\left( x \right)}}-1~\vee ~0\ \ \ \ \left( 2 \right)\) равносильно следующей системе: \(\displaystyle \left\{ \begin{array}{l}\left( h\left( x \right)-1 \right)g\left( x \right)~\ \vee \ ~0\\h\left( x \right)>0\end{array} \right.\)
Неравенство \(\displaystyle f{{\left( x \right)}^{h\left( x \right)}}~\vee ~g{{\left( x \right)}^{h\left( x \right)}}\ \ \ \left( 3 \right)\) равносильно следующей системе: \(\displaystyle \left\{ \begin{array}{l}\left( f\left( x \right)-g\left( x \right) \right)h\left( x \right)~\vee ~0\\f\left( x \right)>0\\g\left( x \right)>0\end{array} \right.\)
Я объясню тебе, откуда берутся эти правила. Например, рассмотрим первое из перечисленных неравенств.
\(\displaystyle h{{\left( x \right)}^{g\left( x \right)}}~\vee ~h{{\left( x \right)}^{f\left( x \right)}}\)
То, что \(\displaystyle h\left( x \right)>0\) следует непосредственно из определения основания. Как же получилось первое неравенство?
В частности, если \(\displaystyle 0<h\left( x \right)<1\), то неравенство \(\displaystyle h{{\left( x \right)}^{g\left( x \right)}}>~h{{\left( x \right)}^{f\left( x \right)}}\) влечет за собой \(\displaystyle g\left( x \right)<f\left( x \right)\).
С другой стороны, так как \(\displaystyle h\left( x \right)-1<0\), то неравенство
\(\displaystyle \left(g\left( x \right)-f\left( x \right) \right)\left( h\left( x \right)-1 \right)>0\) имеет место только тогда, когда \(\displaystyle g\left( x \right)-f\left( x \right)<0\) или \(\displaystyle g\left( x \right)<f\left( x \right)\).
Получили, что при \(\displaystyle 0<h\left( x \right)<1\) неравенства \(\displaystyle h{{\left( x \right)}^{g\left( x \right)}}>~h{{\left( x \right)}^{f\left( x \right)}}\) и \(\displaystyle \left( g\left( x \right)-f\left( x \right) \right)\left( h\left( x \right)-1 \right)>0\) равносильны (учитывая, конечно, ОДЗ на основание).
Аналогично ты можешь получить, что эти же неравенства будут равносильны и при \(\displaystyle h\left( x \right)>1\). Аналогичным образом получаются и все другие системы неравенств.
Давай вернемся к нашему примеру. Я напомню тебе его:
\(\displaystyle {{\left| {x} -3 \right|}^{\frac{{{x}^{2}}-8x+15}{{x} -2}}}>1\)
Смотрим, к неравенству какого типа он относится? А к вот такому: \(\displaystyle h{{\left( x \right)}^{g\left( x \right)}}-1>~0\). Значит, решить его, это все равно, что решить вот такую систему
\(\displaystyle \left\{ \begin{array}{l}\left( \left| {x} -3 \right|-1 \right)\frac{{{x}^{2}}-8x+15}{{x} -2}>0\\\left| {x} -3 \right|>0\end{array} \right.\)
Давай вначале решим нижнее неравенство: так как по определению модуль – число неотрицательное, то \(\displaystyle \left| {x} -3 \right|>0\) всюду, кроме \(\displaystyle x=3\) – та точка, где модуль нулевой. Тогда исходная система равносильна
\(\displaystyle \left\{ \begin{array}{l}\left( \left| {x} -3 \right|-1 \right)\frac{{{x}^{2}}-8x+15}{{x} -2}>0\\x\ne 3\end{array} \right.\)
Теперь нужно решить сложное первое неравенство. Опять-таки, нам нужно разбить его, анализируя два случая. Каких? Что у нас дает эти случаи?
Это опять-таки модуль! Если \(\displaystyle x>3\), то \(\displaystyle \left| {x} -3 \right|=\left( {x} -3 \right)\), а если же \(\displaystyle x<3\), то \(\displaystyle \left| {x} -3 \right|=-\left( {x} -3 \right)=3-x\).
Объединим эти условия, записав новую систему:
\(\displaystyle \left\{ \begin{array}{l}\left[ \begin{array}{l}\left\{ \begin{array}{l}\left( {x} -4 \right)\frac{{{x}^{2}}-8x+15}{{x} -2}>0\\x>3\end{array} \right.\\\left\{ \begin{array}{l}\left( 2-x \right)\frac{{{x}^{2}}-8x+15}{{x} -2}>0\\x<3\end{array} \right.\end{array} \right.\\x\ne 3\end{array} \right.\)
Ну что же, теперь наша цель – решить каждую из этих систем в совокупности. Начнем?
\(\displaystyle \left\{ \begin{array}{l}\left( {x} -4 \right)\frac{{{x}^{2}}-8x+15}{{x} -2}>0\\x>3\end{array} \right.\)
\(\displaystyle {{x}^{2}}-8x+15=\left( {x} -3 \right)\left( {x} -5 \right)\)
\(\displaystyle \frac{\left( {x} -3 \right)\left( {x} -5 \right)\left( {x} -4 \right)}{{x} -2}>0\)
Решим неравенство методом интервалов:
\(\displaystyle x\in \left( -\infty ;2 \right)\mathop{\cup }^{}\left( 3;4 \right)\mathop{\cup }^{}\left( 5;+\infty \right)\)
Однако, надо учесть, что \(\displaystyle x>3\). Тогда первая система имеет следующее множество решений:
\(\displaystyle x\in \left( 3;4 \right)\mathop{\cup }^{}\left( 5;+\infty \right)\)
Теперь черед второй системы.
\(\displaystyle \left\{ \begin{array}{l}\left( 2-x \right)\frac{{{x}^{2}}-8x+15}{{x} -2}>0\\x<3\end{array} \right.\)
Так как \(\displaystyle 2-x\) и \(\displaystyle {x} -2\) отличаются только знаком, то при любых \(\displaystyle x\ne 2\) имеем:
\(\displaystyle \frac{2-x}{{x} -2}=-1\). Тогда систему я перепишу в следующем виде:
\(\displaystyle \left\{ \begin{array}{l}{{x}^{2}}-8x+15<0\\x<3\\x\ne 2\end{array} \right.\)
Решаю методом интервалов:
\(\displaystyle {{x}^{2}}-8x+15<0\)
\(\displaystyle x\in \left( 3;5 \right)\)
В то же время второе неравенство говорит нам о том, что \(\displaystyle x<3\)! Тогда делаем вывод: данная система решений не имеет. Отсюда решением совокупности
\(\displaystyle \left[ \begin{array}{l}\left\{ \begin{array}{l}\left( {x} -4 \right)\frac{{{x}^{2}}-8x+15}{{x} -2}>0\\x>3\end{array} \right.\\\left\{ \begin{array}{l}\left( 2-x \right)\frac{{{x}^{2}}-8x+15}{{x} -2}>0\\x<3\end{array} \right.\end{array} \right.\)
будет решение первой системы:
\(\displaystyle x\in \left( 3;4 \right)\mathop{\cup }^{}\left( 5;+\infty \right)\)
Поскольку здесь уже учтено, что \(\displaystyle x\ne 3\), то решение системы
\(\displaystyle \left\{ \begin{array}{l}\left[ \begin{array}{l}\left\{ \begin{array}{l}\left( {x} -4 \right)\frac{{{x}^{2}}-8x+15}{{x} -2}>0\\x>3\end{array} \right.\\\left\{ \begin{array}{l}\left( 2-x \right)\frac{{{x}^{2}}-8x+15}{{x} -2}>0\\x<3\end{array} \right.\end{array} \right.\\x\ne 3\end{array} \right.\)
Совпадает с решением совокупности и будет
\(\displaystyle x\in \left( 3;4 \right)\mathop{\cup }^{}\left( 5;+\infty \right)\)
Ответ: \(\displaystyle x\in \left( 3;4 \right)\mathop{\cup }^{}\left( 5;+\infty \right)\).
Теперь попробуй проделать похожие выкладки вот для такого примера (он покажется тебе легким по сравнению с предыдущим):
\(\displaystyle {{\left( x+2 \right)}^{x}}>{{\left( x+2 \right)}^{{{x}^{2}}+2}}\)
и сравни свой ответ с моим:
\(\displaystyle x\in \left( -2;-1 \right)\).
Теперь ты вполне можешь справиться с решением многих, очень многих примеров 19 задачи.
Решай, не боясь их внешнего вида, на самом деле стоит лишь немного подумать, и все окажется простым! Я уверен, теперь у тебя все получится!
Сравнивай ответы и гордись своими приобретенными знаниями!
Метод №5. Анализ монотонности функций
Последним по номеру, но не по значимости, является решение неравенства методом анализа монотонности функции. Данный метод достаточно хитер: не всегда ясно, когда его следует применять. Я бы прибегал к нему в последнюю очередь.
Однако, если твое неравенство является смешанным то данного метода уже, увы, не избежать.
Например \({{2}^{x}}>1-x\) – смешанное неравенство.
Оно включает в себя не только степени, но и линейное выражение \(1-x\)).
В дополнение к уже изложенному выше материалу, рассмотрим такие неравенства, которые не удается решать обыкновенными методами.
К «обыкновенным» обычно относят разложение на множители, замену переменных, элементарные преобразования оснований и т. д.
Далеко не все неравенства можно решить таким образом. Я бы сказал, что большинство тех неравенств, с которыми математики сталкиваются в реальности, не поддаются такому простому решению.
И здесь мы и рассмотрим один из методов решения таких «непростых» неравенств.
Все мои дальнейшие рассуждения будут основаны на таком понятии, как монотонность функции.
Ты уже не раз сталкивался с этим термином. Например, функция \(\displaystyle ~f\left( x \right)=2x+1\) монотонно возрастает на всей числовой прямой, а \(\displaystyle f\left( x \right)=-{{x}^{0,5}}\) — монотонно убывает. Еще раз напомню, что это значит.
Определение:
\(\displaystyle f\left( x \right)\) монотонно возрастает на \(\displaystyle \left[ a,b \right]\), если для любых \(\displaystyle {{x}_{1}}\) и \(\displaystyle {{x}_{2}}\) из этого промежутка из того, что \(\displaystyle {{x}_{1}}<{{x}_{2}}\) следует, что \(\displaystyle f\left( {{x}_{1}} \right)<f\left( {{x}_{2}} \right)\) и наоборот, из того, что \(\displaystyle {{x}_{1}}>{{x}_{2}}\) следует, что \(\displaystyle f\left( {{x}_{1}} \right)>f\left( {{x}_{2}} \right)\).
Определение:
\(\displaystyle f\left( x \right)\) монотонно убывает на \(\displaystyle \left[ a,b \right]\), если для любых \(\displaystyle {{x}_{1}}\) и \(\displaystyle {{x}_{2}}\) из этого промежутка из того, что \(\displaystyle {{x}_{1}}<{{x}_{2}}\) следует, что \(\displaystyle f\left( {{x}_{1}} \right)>f\left( {{x}_{2}} \right)\) и наоборот, из того, что \(\displaystyle {{x}_{1}}>{{x}_{2}}\) следует, что\(\displaystyle f\left( {{x}_{1}} \right)<f\left( {{x}_{2}} \right)\).
Простые рисунки иллюстрируют эти определения:
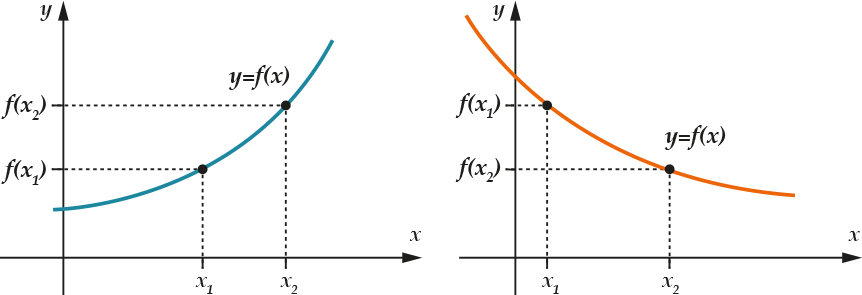
Функция на рисунке слева – монотонно возрастающая, а справа – монотонно убывающая. Теперь обратимся к показательной функции \(\displaystyle f\left( x \right)={{a}^{x}}\), известно, что выполняется следующая теорема:
Если \(\displaystyle a>1\), то функция \(\displaystyle f\left( x \right)={{a}^{x}}\) является монотонно возрастающей, если \(\displaystyle 0<a<1\), то функция \(\displaystyle f\left( x \right)={{a}^{x}}\) является монотонно убывающей.
Также хорошо известно, что имеет место следующее утверждение:
Если \(\displaystyle f\left( x \right)=g\left( x \right)\) и \(\displaystyle f\left( x \right)\) – монотонно возрастающая (или постоянная), а \(\displaystyle g\left( x \right)\) – монотонно убывающая функции (или постоянная) , то уравнение \(\displaystyle f\left( x \right)=g\left( x \right)\) имеет не более одного корня.
Как нам это перефразировать на язык неравенств? Ведь мы решаем именно их, а не уравнения. А делается это довольно просто:
Давай посмотрим на картинку и все сразу поймем:
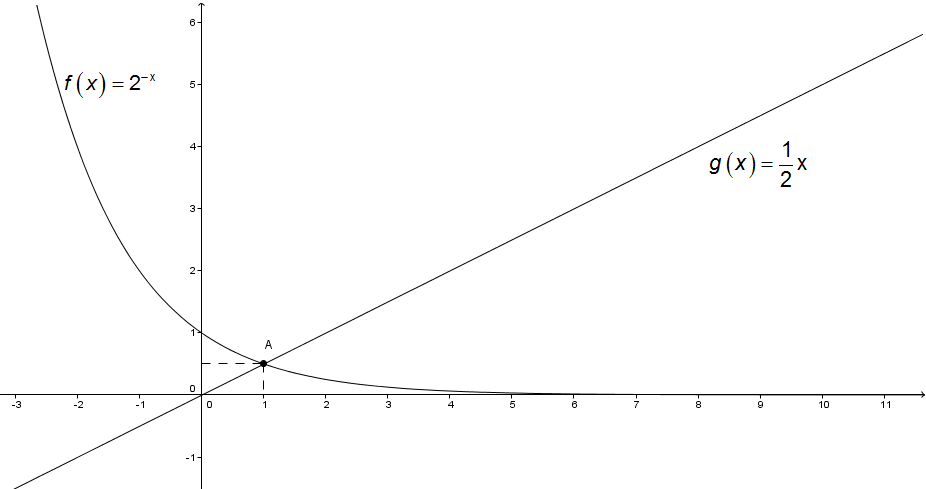
Например, пусть нам необходимо решить неравенство: \(\displaystyle {{2}^{-x}}>\frac{x}{2}\),
Мы видим, что левая часть неравенства есть убывающая функция \(\displaystyle f\left( x \right)={{2}^{-x}}={{0,5}^{x}}\) , а правая – возрастающая.
Тогда находим их (единственную!) точку пересечения. Нашли, это \(\displaystyle x=1\).
Что же мы видим на рисунке? А то, что после того, как \(\displaystyle x>1\) возрастающая функция всюду больше, чем убывающая (график возрастающей лежит выше), а значит, неравенство \(\displaystyle {{2}^{-x}}>\frac{x}{2}\) имеет место при всех \(\displaystyle x<1\).
Мы получаем следующий алгоритм:
Пусть дано неравенство\(\displaystyle f\left( x \right)>g\left( x \right)\), где \(\displaystyle f\left( x \right)\) – убывающая, а \(\displaystyle g\left( x \right)\) – возрастающая. Тогда:
Правило 1. Ищем корень (максимум единственный) уравнения \(\displaystyle f\left( x \right)=g\left( x \right)\)
Если корня нет, то сразу делаем вывод, что всюду \(\displaystyle g\left( x \right)>f\left( x \right)\), а потому исходное неравенство не имеет решений.
Если нашелся корень \(\displaystyle {{x}_{0}}\), то исходное неравенство имеет место при \(\displaystyle x\in \left( -\infty ;{{x}_{0}} \right)\)
Попробуй сам привести алгоритмы для других случаев неравенств. Я уверен, у тебя это без проблем получится. Стоит только нарисовать картинки и внимательно посмотреть на них. Готово? Отлично, тогда у нас есть мощный арсенал для решения самых различных показательных неравенств.
Пример 1:
Решите неравенство: \(\displaystyle {{2}^{x}}+{{3}^{x}}>{{5}^{x}}\).
Разделим обе части на \(\displaystyle {{5}^{x}}\), получим, что:
\(\displaystyle {{\left( \frac{2}{5} \right)}^{x}}+{{\left( \frac{3}{5} \right)}^{x}}>1\)
Слева мы с тобой получили сумму двух убывающих функций. Как ты думаешь, какой будет сумма двух убывающих функций? Правильно, она снова будет убывающей!!
Запомни правило, оно часто помогает выйти из очень затруднительных ситуаций!!
Правило 2. \(\displaystyle Убывающая+убывающая=убывающая\)
\(\displaystyle Возрастающая+возрастающая=возрастающая\)
\(\displaystyle Возрастающая-убывающая=возрастающая\)
\(\displaystyle Убывающая-возрастающая=убывающая\)
Итак, слева у нас сумма двух убывающих функций, а справа – постоянная \(\displaystyle 1\).
Уравнение \(\displaystyle {{\left( \frac{2}{5} \right)}^{x}}+{{\left( \frac{3}{5} \right)}^{x}}=1\) имеет единственный корень \(\displaystyle {{x}_{0}}=1\). Тогда в соответствии с правилом 1 получим \(\displaystyle x\in \left( -\infty ;1 \right)\).
Теперь рассмотрим еще один пример.
Пример 2:
\(\displaystyle x{{4}^{x}}>4\)Рассмотрим 2 случая:
1) Пусть \(\displaystyle x>0\), тогда разделим обе части неравенства на положительный \(\displaystyle x\):
\(\displaystyle {{4}^{x}}>\frac{4}{x}\)
Слева у нас стоит возрастающая функция, а справа – убывающая при \(\displaystyle x>0\).
Корень уравнения \(\displaystyle {{4}^{x}}=\frac{4}{x}\) равен \(\displaystyle 1\) и является единственным. Тогда при \(\displaystyle x>0\) неравенство имеет решение: \(\displaystyle x>1\).
2) Теперь пусть \(\displaystyle x<0\), разделю обе части \(\displaystyle x{{4}^{x}}>4\) на отрицательный \(\displaystyle x\). Получу \(\displaystyle {{4}^{x}}<\frac{4}{x}\).
При \(\displaystyle x<0\), но левая часть неравенства всегда положительна, в то время как правая – всегда отрицательна. Тогда \(\displaystyle {{4}^{x}}<\frac{4}{x}\) не имеет решений при отрицательных \(\displaystyle x\). И ответом будет \(\displaystyle x\in \left( 1;+\infty \right)\).
Самостоятельно реши примеры на анализ монотонности функций
- \(\displaystyle {{2}^{\sqrt{x}}}+{{3}^{\sqrt{x}+1}}+{{4}^{\sqrt{2}+2}}>20\)
- \(\displaystyle {{2}^{{{x}^{2}}-4x+9}}<\frac{1}{1+\left| x-3 \right|}\)
Решение:
Пример 1. Давай разберемся. Первый пример достаточно легкий и решается технично и быстро.
Сразу заметим, что \(\displaystyle x\ge 0\) (свойство корня).
Ясно, что слева записана сумма возрастающих функций, поэтому все выражение слева возрастает, тогда как справа – постоянно.
Единственная точка, в которой они совпадают – \(\displaystyle \ x=0\).
Ответ: \(\displaystyle x\in \left( 0;+\infty \right)\).
Пример 2. Второй пример потруднее, здесь появляется выражение, зависящее от модуля. Рассмотрим его подробнее.
Во-первых, ясно, что выражение справа всегда не больше, чем \(\displaystyle 1\). Причем равенство достигается при \(\displaystyle x=3\).
Далее, при \(\displaystyle x>3\) выражение принимает форму \(\displaystyle \frac{1}{x-2}\), а при \(\displaystyle x<3\) мы имеем:
\(\displaystyle \frac{1}{4-x}\), таким образом, всюду правая часть не больше \(\displaystyle 1\), причем при \(\displaystyle x>3\) функция монотонно возрастает, а при \(\displaystyle x<3\) – монотонно убывает.
Рассмотрим теперь показатель выражения слева:
\(\displaystyle {{x}^{2}}-4x+9\), ясно, что дискриминант данного выражения равен \(\displaystyle -20<0\), но \(\displaystyle g\left( x \right)=~{{x}^{2}}-4x+9\) – парабола с ветвями, направленными вверх с вершиной \(\displaystyle {{x}_{0}}=\frac{4}{2}=2\).
В этой точке функция достигает своего наименьшего значения \(\displaystyle g\left( 2 \right)=~{{2}^{2}}-4\cdot 2+9=5\), а значит наименьшее значение \(\displaystyle {{2}^{{{x}^{2}}-4x+9}}\) равно \(\displaystyle {{2}^{5}}=32\).
В то время, как наибольшее значение правой части равно \(\displaystyle 1\).
Таким образом, левая часть всюду больше правой части и исходное неравенство не имеет решений.
Бонусы. Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №15. Показательные уравнения и неравенства. Сравнение чисел. Логарифмы
В этом видео мы научимся решать сложные показательные уравнения и неравенства.
Чаще всего они сводятся к квадратным или рациональным.
В сложных неравенствах нам никто не гарантирует, что концы интервалов получатся «красивыми» — частенько там возникают логарифмы.
Поэтому, чтобы знать, как эти точки располагаются на числовой прямой, нам необходимо уметь сравнивать значения логарифмов (друг с другом и с «обычными» числами). Это мы также научимся делать.
ЕГЭ №15. Смешанные неравенства. Логарифмические и тригонометрические
«Задачу №15 мы на курсе уже научились решать: разобрали по косточкам и показательные, и логарифмические (в том числе с переменными основаниями), и смешанные неравенства.
Ну и системы неравенств не забыли.
Бонусом прошлись по иррациональным неравенствам и неравенствам с модулем.
Но погодите, не выдыхайте пока. Поиграем в слабо! А слабо скрестить логарифмы с тригонометрией?
Этим и займемся в задаче на логарифмы с разными основаниями. Мы решим эту сложную задачу 2-мя способами!»
Подготовка к профильному ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Как то мне непонятен метод декомпозиции, именно объяснение (1)
В частности эта строка, если 0<h(x) h(x)f(x) влечет за собой f(x)<g(x).
Разве в равносильном неравенстве не должен быть обратный знак?
Даниил, да, там была опечатка, должно быть наоборот, g(x) < f(x). Спасибо, что заметил!
!!!!!!!