График квадратичной функции
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое квадратичная функция.
Проверь себя, ответь на эти вопросы:
- Как выглядит квадратичная функция в общем виде (формула)?
- Как называется график квадратичной функции?
- Как влияет старший коэффициент на график квадратичной функции?
Если ты сходу смог ответить, продолжай читать.
Если хоть один вопрос вызвал затруднения, повтори тему «Квадратичная функция».
А мы начинаем!
График квадратичной функции — коротко о главном
Определение
Квадратичная функция – функция вида \( y=a{{x}^{2}}+bx+c\), где \( a\ne 0\), \( b\) и \( c\) – любые числа (коэффициенты), \( c\) – свободный член.
График квадратичной функции – парабола.
Если коэффициент \( \displaystyle a<0\), ветви параболы направлены вниз, если \( \displaystyle a>0\) – ветви параболы направлены вверх.
Чем больше значение \( \displaystyle a\) (по модулю), тем у́же становится парабола (ветви становятся более крутыми). И наоборот, чем меньше \( \displaystyle a\), тем парабола шире.
Вершина параболы
\( \displaystyle {{x}_{в}}=\frac{-b}{2a}\), т.е. чем больше \( \displaystyle b\), тем левее смещается вершина параболы.
Подставляем \( \displaystyle {{x}_{в}}\) в функцию \( y=a{{x}^{2}}+bx+c\), и получаем:
\( \displaystyle {{y}_{в}}=-\frac{{{b}^{2}}-4ac}{4a^2}\), т.е. чем \( \displaystyle b\) больше по модулю, тем выше будет вершина параболы
Свободный член \( \displaystyle c\) – это координата пересечения параболы с осью ординат.
Квадратичная функция и её коэффициенты
Итак, ты уже умеешь обращаться с квадратичной функцией, анализировать ее график и строить график по точкам.
Ну что же, вот она: \( y=a{{x}^{2}}+bx+c\).
Давай вкратце вспомним, что делают коэффициенты.
- Старший коэффициент \( \displaystyle a\) отвечает за «крутизну» параболы, или, по-другому, за ее ширину: чем больше \( \displaystyle a\), тем парабола у́же (круче), а чем \( \displaystyle a\) меньше, тем парабола шире (более пологая).
- Свободный член \( \displaystyle c\) – это координата пересечения параболы с осью ординат.
- А коэффициент \( \displaystyle b\) каким-то образом отвечает за смещение параболы от центра координат. Вот об этом сейчас подробнее.
С чего мы всегда начинаем строить параболу? Какая у нее есть отличительная точка?
Это вершина. А как найти координаты вершины, помнишь?
Абсцисса ищется по такой формуле:
\( {{x}_{в}}=\frac{-b}{2a}\).
Вот так: чем больше \( \displaystyle b\), тем левее смещается вершина параболы.
Ординату вершины можно найти, подставив \( {{x}_{в}}\) в функцию:
\( {{y}_{в}}=a{{x}_{в}}^{2}+b{{x}_{в}}+c\).
Подставь сам и посчитай. Что получилось?
Если сделать все правильно и максимально упростить полученное выражение, получится:
\( {{y}_{в}}=-\frac{{{b}^{2}}-4ac}{4a}\).
Получается, что чем \( \displaystyle b\) больше по модулю, тем выше будет вершина параболы.
Перейдем, наконец, к построению графика.
Самый простой способ – строить параболу, начиная с вершины.
Пример №1
Построить график функции \( y=\frac{1}{2}{{x}^{2}}+2{x}-1\).
Решение:
Для начала определим коэффициенты: \( a=\frac{1}{2};\text{ }b=2;\text{ }c=-1\).
Теперь вычислим координаты вершины:
\( {{x}_{в}}=\frac{-b}{2a}=\frac{-2}{2\cdot \frac{1}{2}}=-2\) \( {{y}_{в}}=-\frac{{{b}^{2}}-4ac}{4a}=-\frac{4+2}{2}=-3\)А теперь вспоминаем: все параболы с одинаковым старшим коэффициентом выглядят одинаково.
Значит, если мы построим параболу \( y=\frac{1}{2}{{x}^{2}}\) и переместим ее вершиной в точку \( \left( -2;-3 \right)\), получится нужный нам график:
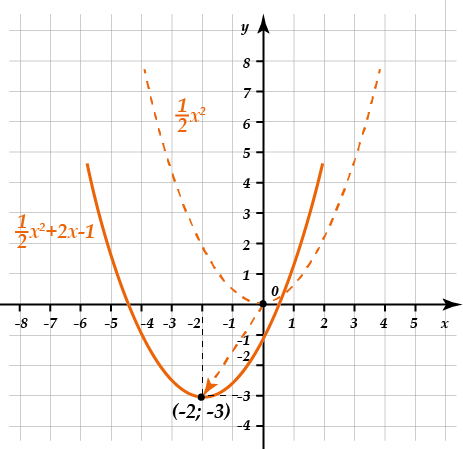
Просто, правда?
Остается только один вопрос. Как быстро рисовать параболу?
Как быстро рисовать график квадратичной функции — параболу?
Даже если мы рисуем параболу с вершиной в начале координат, все равно приходится строить ее по точкам, а это долго и неудобно. А ведь все параболы выглядят одинаково, может, есть способ ускорить их рисование?
Когда я учился в школе, учительница математики сказала всем вырезать из картона трафарет в форме параболы, чтобы быстро ее чертить. Но с трафаретом везде ходить не получится, да и на экзамен его взять не разрешат. Значит, не будем пользоваться посторонними предметами, а будем искать закономерность.
Рассмотрим простейшую параболу \( y={{x}^{2}}\). Построим ее по \( \displaystyle 7\) точкам:
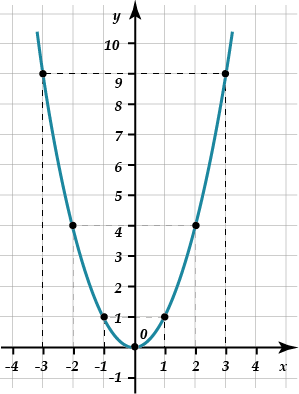
Закономерность здесь такая.
Если из вершины сместиться вправо (вдоль оси \( \displaystyle Ox\)) на \( \displaystyle 1\), и вверх (вдоль оси \( \displaystyle Oy\)) на \( \displaystyle 1\), то попадем в точку параболы.
Дальше: если из этой точки сместиться вправо на \( \displaystyle 1\) и вверх на \( \displaystyle 3\), снова попадем в точку параболы.
Дальше: вправо на \( \displaystyle 1\) и вверх на \( \displaystyle 5\). Дальше что?
Вправо на \( \displaystyle 1\) и вверх на \( \displaystyle 7\).
И так далее: смещаемся на \( \displaystyle 1\) вправо, и на следующее нечетное число вверх.
То же самое потом проделываем с левой веткой (ведь парабола симметрична, то есть ее ветви выглядят одинаково):
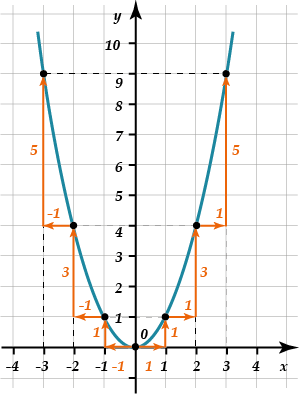
Отлично, это поможет построить из вершины любую параболу со старшим коэффициентом, равным \( \displaystyle 1\).
Пример построения параболы быстрым способом
Например, нам стало известно, что вершина параболы находится в точке \( \displaystyle \left( 1;-2 \right)\). Построй (самостоятельно, на бумаге) эту параболу.
Построил?
Должно получиться так:
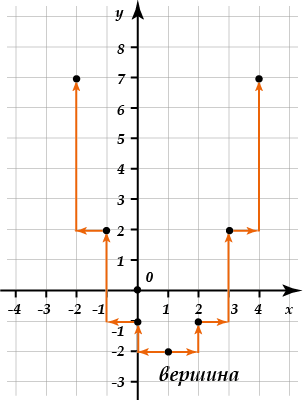
Теперь соединяем полученные точки:
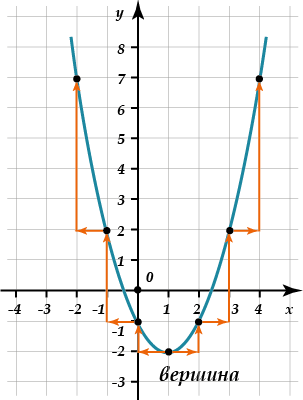
Вот и все.
ОК, ну что же, теперь строить только параболы с \( \displaystyle a=1\)?
Конечно, нет. Сейчас разберемся, что с ними делать, если \( \displaystyle a\ne 1\).
Три типичных случая построения параболы
Cлучай 1. \( a=-1\).
То есть функция выглядит как \( y=-{{x}^{2}}\). Ну что же здесь сложного? Просто переворачиваем параболу рогами вниз, и все. То есть, теперь будем двигаться так:
- \( 1\) вправо – \( 1\) вниз
- \( 1\) вправо – \( 3\) вниз
- \( 1\) вправо – \( 5\) вниз и т. д.
И то же самое, только влево.
Случай 2. \( a>1\).
Что делать, если, например, \( a=2\)?
Все просто: начинаем так же: \( 1\) вправо, но когда дело доходит до «вверх», любое число увеличиваем в \( 2\) раза:
- \( 1\) вправо – \( 2\) вверх
- \( 1\) вправо – \( 6\) вверх
- \( 1\) вправо – \( 10\) вверх и т. д.
Аналогично в случае \( a<-1\):
- \( 1\) вправо – \( 2\) вниз
- \( 1\) вправо – \( 6\) вниз
- \( 1\) вправо – \( 10\) вниз и т. д.
В общем случае так:
- \( 1\) вправо – \( a\) вверх
- \( 1\) вправо – \( 3a\) вверх
- \( 1\) вправо – \( 5a\) вверх и т. д.
Если \( a<0\), то вместо «вверх» делаем «вниз».
Случай 3. А если \( -1<a<1\)?
Принцип тот же: каждый шаг вправо или влево сопровождается шагом вверх или вниз, равным какому-то нечетному числу, умноженному на \( a\).
Но отмерять нецелые (дробные) отрезки всегда лень. Поэтому иногда удобнее сделать по-другому: шаг вправо или влево делать не \( 1\), а \( \frac{1}{a}\).
Тогда вверх/вниз придется смещаться на целые \( \frac{1}{a}\), \( \frac{3}{a}\), \( \frac{5}{a}\), \( \frac{7}{a}\), … клеток.
Например: построим график \( y=-\frac{1}{3}{{x}^{2}}\). Будем откладывать:
- вправо \( 3\) – вниз \( 3\)
- вправо \( 3\) – вниз \( 9\)
- вправо \( 3\) – вниз \( 15\) и т. д.
и затем то же самое влево.
Отлично, параболу рисовать научились, давай теперь потренируемся на настоящих функциях.
4 задачи на построение графика функции
Нарисуй 4 графика следующих функций:
- \( y={{x}^{2}}-2{x}+3\)
- \( y=-2{{x}^{2}}+12{x}-20\)
- \( y=\frac{{{x}^{2}}}{2}-2{x}-2\)
- \( y={{x}^{2}}+5{x}+3\)
Ответы:
1. \( {{x}_{в}}=\frac{-b}{2a}=1;\text{ }{{y}_{в}}=-\frac{{{b}^{2}}-4ac}{4a}=2\):
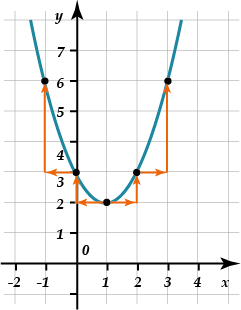
2. \( {{x}_{в}}=3;\text{ }{{y}_{в}}=-2\)
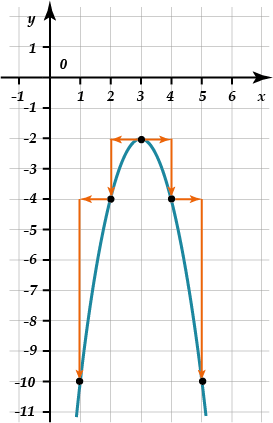
3. Вершина: \( {{x}_{в}}=2;\text{ }{{y}_{в}}=-4\).
Помнишь, что делать, если старший коэффициент меньше \( \displaystyle 1\)?
Смотрим на знаменатель дроби: он равен \( \displaystyle 2\). Значит, будем двигаться так:
4. Вершина: \( {{x}_{в}}=-2,5;\text{ }{{y}_{в}}=-3,25\).
Ой, а что с этим делать? Как отмерять клетки, если вершина где-то между линиями?..
А мы схитрим.
Рассмотрим еще один способ записи квадратичной функции: выделение полного квадрата. Этот способ был подробно описан в теме «Квадратные уравнения».
Выделение полного квадрата
Напомню, что мы можем представить функцию \( y=a{{x}^{2}}+bx+c\) в таком виде:
\( y=a{{\left( x-p \right)}^{2}}+q\).
Например: \( y={{x}^{2}}-6x+5={{\left( x-3 \right)}^{2}}-4\).
Или: \( 2{{x}^{2}}+6x+1=2{{\left( x+1,5 \right)}^{2}}-3,5\).
Что это нам дает?
Дело в том, что число, которое вычитается из \( \displaystyle x\) в скобках (\( \displaystyle p\)) – это абсцисса вершины параболы, а слагаемое за скобками (\( \displaystyle q\)) – ордината вершины.
Это значит, что, построив параболу \( y=a{{x}^{2}}\), нужно будет просто сместить ось \( \displaystyle Oy\) на \( \displaystyle p\) влево и ось \( \displaystyle Ox\) на \( q\) вниз.
Пример: построим график функции \( y=0,5{{x}^{2}}+2x+1\).
Выделим полный квадрат:
\( y=0,5\left( {{x}^{2}}+4x \right)+1=0,5\left( {{x}^{2}}+4x+4-4 \right)+1=0,5\left( {{x}^{2}}+4x+4 \right)-2+1=0,5{{\left( x+2 \right)}^{2}}-1\)
Какое число вычитается из \( \displaystyle x\) в скобках? Это \( \displaystyle -2\) (а не \( \displaystyle 2\), как можно решить, не подумав).
Итак, строим параболу \( y=0,5{{x}^{2}}\):
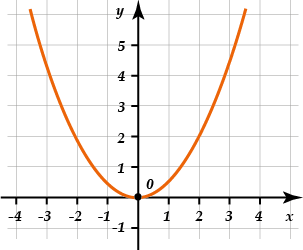
Теперь смещаем ось \( \displaystyle Ox\) на \( \displaystyle -1\) вниз, то есть на \( \displaystyle 1\) вверх:
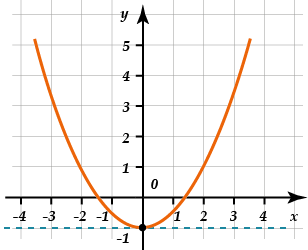
А теперь – \( \displaystyle Oy\) на \( \displaystyle -2\) влево, то есть на \( \displaystyle 2\) вправо:
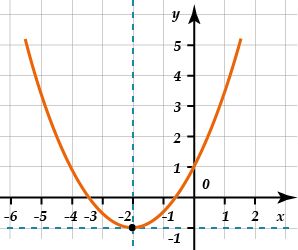
Вот и все. Это то же самое, как переместить параболу \( y=0,5{{x}^{2}}\) вершиной из начала координат в точку \( \displaystyle (-2;-1)\), только прямые оси двигать намного легче, чем кривую параболу.
Теперь, как обычно, сам.
Еще два примера на самостоятельную работу
- \( y=2{{x}^{2}}-8x+3\)
- \( y=-{{x}^{2}}-4x+2\)
И не забывай стирать ластиком старые оси!
Я в качестве ответов для проверки напишу тебе ординаты вершин этих парабол:
- \( \displaystyle -5\)
- \( \displaystyle 6\)
Все сошлось?
Если да, то ты молодец! Уметь обращаться с параболой – очень важно и полезно, и здесь мы выяснили, что это совсем не трудно.
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
Выделение полного квадрата
Посмотри это видео и ты научишься выделять полный квадрат на автомате!
Этот навык помимо построения параболы, поможет вам решать квадратные уравнения, раскладывать выражение на множители, разобраться с с уравнением окружности в задаче с параметром (18-я задача), которая дает целых 4 первичных балла.
В общем, метод выделения полного квадрата — бесценный навык.
Берите тетрадку, ручку и смотрите видео. Алексей разберет 8 примеров! Слушайте условие, ставьте на паузу, решайте и потом сравнивайте с тем, как решил Алексей.
Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)
Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.
Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики.
На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях).
Мы рассмотрим:
- степенную функцию (линейную, квадратичную, обратную зависимость, корни),
- тригонометрические и обратные тригонометрические,
- показательную и
- логарифмическую функции.
Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Чем больше значение b по модулю, тем меньше значение Y, потому что там стоит — перед дробью (формулой).
Некоторые комментарии прошлых лет к этой статье:
Добрые человек
27 октября 2017
Хороший сайт, очень удобно и понятно ,спасибо вам)
Светлана
14 ноября 2017
Спасибо. Всё встало на свои места. А как на счёт остальных функций?
Юлия Овчиникова
16 февраля 2020
В случае со смещением на 0,5 и 0,25 происходит изменение не на нечетное количество клеток, а четное. Сначала отмечаем две ближайшие клетки, а потом: 2,4,6, и т.д.
Алексей Шевчук
19 февраля 2020
Юлия, да, это верно, этим способом можно пользоваться. Но я решил не включать его в статью, чтобы не создать кашу из разных, но похожих друг на друга, алгоритмов. Вполне достаточно одного способа рисовать параболу + смещения графика или осей.