Обратная пропорциональность. Гипербола
Сейчас мы будем говорить об обратной пропорциональности, или другими словами об обратной зависимости, как о функции.
Мы закрепим понятие функции и научимся работать с коэффициентами и графиками.
А еще мы разберем несколько примеров построения графика функции — гиперболы.
Начнём!
Обратная пропорциональность — коротко о главном
Определение:
Функция, описывающая обратную пропорциональность, – это функция вида \( \displaystyle y=\frac{k}{x-a}+b \), где \( k\ne 0\), \( x\ne 0\) и \( x\ne а\)
По-другому эту функцию называют обратной зависимостью.
Область определения и область значений функции:
\( D\left( y \right)=\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\) или, что то же самое, \( D\left( y \right)=\mathbb{R}\backslash \left\{ 0 \right\}\)
\( E\left( y \right)=\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\) или \( E\left( y \right)=\mathbb{R}\backslash \left\{ 0 \right\}\).
График обратной пропорциональности (зависимости) – гипербола.
Коэффициент \( \displaystyle k\)
\( \displaystyle k\) – отвечает за «пологость» и направление графика. Чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок).
Знак коэффициента \( \displaystyle k\) влияет на то, в каких четвертях расположен график:
если \( \displaystyle k>0\), то ветви гиперболы расположены в \( \displaystyle I\) и \( \displaystyle III\) четвертях;
если \( \displaystyle k<0\), то во \( \displaystyle II\) и \( \displaystyle IV\).
Коэффициент \( \displaystyle a\)
Если внимательно посмотреть на знаменатель, видим, что \( \displaystyle a\) – это такое число, которому не может равняться \( \displaystyle x\).
То есть \( x=a\) – это вертикальная асимптота, то есть вертикаль, к которой стремится график функции
Коэффициент \( b\)
Число \( b\) отвечает за смещение графика функции вверх на величину \( b\), если \( b>0\), и смещение вниз, если \( b<0\).
Следовательно, \( y=b\) – это горизонтальная асимптота.
Алгоритм построения графика функции \( \displaystyle y=\frac{k}{x-a}+b\)
- Определяем коэффициенты \( \displaystyle k\), \( \displaystyle a\) и \( \displaystyle b\).
- Строим график функции \( \displaystyle y=\frac{k}{x}\) (сначала по 3-4 точкам правую ветвь, потом симметрично рисуем левую ветвь).
- График должен быть сдвинут вправо на \( \displaystyle a\). Но проще двигать не график, а оси, так что ось \( \displaystyle Oy\) сдвигаем влево на \( \displaystyle a\).
- График должен быть сдвинут вверх на \( \displaystyle b\). Но проще двигать не график, а оси, так что ось \( \displaystyle Ox\) сдвигаем вниз на \( \displaystyle b\).
- Старые оси (прямые, которые служили нам осями в пункте 2) оставляем в виде пунктирных линий. Это теперь просто вертикальная и горизонтальная асимптоты.
Что такое функция
Ты помнишь, что функция – это определенного рода зависимость?
Если ты еще не читал тему «Функции», настоятельно рекомендую бросить все и прочитать, ведь нельзя изучать какую-либо конкретную функцию, не понимая, что это такое – функция.
Также очень полезно перед началом этой темы освоить две более простые функции: линейную и квадратичную.
Там ты закрепишь понятие функции и научишься работать с коэффициентами и графиками.
Ну и на всякий случай немного повторим…
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Что значит «допустимому значению»?
Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции»!
Все дело в понятии «область определения»: для некоторых функций не все аргументы можно подставить в зависимость. Например, для функции \( y=\sqrt{x}\) отрицательные значения аргумента \( x\) – недопустимы.
Функция, описывающая обратную зависимость
Это функция вида \( \displaystyle y=\frac{k}{x}\), где \( k\ne 0\).
По-другому ее называют обратной пропорциональностью: увеличение аргумента вызывает пропорциональное уменьшение функции.
Давай определим область определения. Чему может быть равен \( x\)? Или, по-другому, чему он не может быть равен?
Единственное число, на которое нельзя делить – это \( 0\), поэтому \( x\ne 0\):
\( D\left( y \right)=\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\)
или, что то же самое,
\( D\left( y \right)=\mathbb{R}\backslash \left\{ 0 \right\}\)
Такая запись означает, что \( x\) может быть любым числом, кроме \( 0\).
- Знак «\( \mathbb{R}\)» обозначает множество действительных чисел, то есть всех возможных чисел.
- Знаком «\( \backslash \)» обозначается исключение чего-нибудь из этого множества (аналог знака «минус»).
- Число \( 0\) в фигурных скобках означает просто число \( 0\).
Получается, что из всех возможных чисел мы исключаем \( 0\)).
Множество значений функции, оказывается, точно такое же: ведь если \( k\ne 0\), то на что бы мы его не делили, \( 0\) не получится:
\( E\left( y \right)=\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\) или \( E\left( y \right)=\mathbb{R}\backslash \left\{ 0 \right\}\).
Также возможны некоторые вариации формулы \( y=\frac{k}{x}\). Например, \( y=\frac{k}{x+a}\) – это тоже функция, описывающая обратную зависимость.
Определи самостоятельно область определения и область значений этой функции. Должно получиться:
- \( D\left( y \right)=\left( -\infty ;-a \right)\cup \left( -a;+\infty \right)\)
- \( E\left( y \right)=\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\).
Давай посмотрим на такую функцию: \( \displaystyle y=\frac{x-5}{{{x}^{2}}-25}\).
Является ли она обратной зависимостью?
На первый взгляд сложно сказать: ведь при увеличении \( x\) увеличивается и знаменатель дроби, и числитель, так что непонятно, будет ли функция уменьшаться, и если да, то будет ли она уменьшаться пропорционально?
Чтобы понять это, нам необходимо преобразовать выражение таким образом, чтобы в числителе не было переменной:
\( \displaystyle y=\frac{x-5}{{{x}^{2}}-25}=\frac{x-5}{\left( x-5 \right)\left( x+5 \right)}=\frac{1}{x+5},\text{ }x\ne 5\).
Действительно, мы получили обратную зависимость, но с оговоркой: \( x\ne 5\).
Почему так? А потому, что выражение \( \left( x-5 \right)\) было в исходном выражении в знаменателе, поэтому если мы возьмём значение \( x=5\) и подставим его в исходную функцию (а ведь именно её нам нужно исследовать), то что мы получим?
Ноль, делённый на ноль. Но ведь на ноль нельзя делить ничего, даже другой ноль. Поэтому \( x\) никак не может быть равен \( 5\).
Но почему тогда мы также не пишем \( x\ne -5\)? Оно ведь тоже в знаменателе!
А всё потому, что оно как было в знаменателе, так там и осталось, следовательно мы и так видим, что такое значение икса невозможно.
А поэтому — зачем лишний раз писать? Да-да, математики — народ ленивый, без надобности напрягаться не станут:)
Вот еще пример: \( \displaystyle y=\frac{x+2}{x-3}\).
Тут сложнее: ведь числитель и знаменатель теперь уж точно не сокращаются. Но все-же мы можем попробовать:
\( \displaystyle y=\frac{x+2}{x-3}=\frac{x-3+3+2}{x-3}=\frac{\left( x-3 \right)+5}{x-3}\)
Ты понял, что я сделал? В числителе я добавил и вычел одно и то же число (\( 3\)), таким образом я вроде бы ничего не изменил, но теперь в числителе есть часть, равная знаменателю.
Теперь я почленно поделю, то есть разобью эту дробь на сумму двух дробей:
\( \displaystyle y=\frac{\left( x-3 \right)+5}{x-3}=\frac{x-3}{x-3}+\frac{5}{x-3}\)
(и правда, если привести то что у меня получилось к общему знаменателю, получится как-раз наша начальная дробь):
\( \displaystyle y=\underbrace{\left( \frac{x-3}{x-3} \right)}_{=1}+\frac{5}{x-3}=1+\frac{5}{x-3}.\)
Ух ты! Снова получается обратная пропорциональность, только теперь к ней еще прибавляется число \( \displaystyle 1\).
Этот метод нам очень пригодится позже при построении графиков.
А теперь самостоятельно приведи выражения к виду обратной зависимости
- \( \displaystyle y=\frac{x-1}{x+2}\)
- \( \displaystyle y=\frac{x+5}{{{x}^{2}}+4{x}-5}\)
- \( \displaystyle y=\frac{2{x}-3}{x+1}\)
Решения
Пример 1
\( \displaystyle y=1-\frac{3}{x+2}\)Пример 2
Здесь нужно вспомнить, как квадратный трехчлен раскладывается на множители (это подробно описано в теме «Разложение на множители»).
Напомню, что для этого надо найти корни соответствующего квадратного уравнения: \( \displaystyle {{x}^{2}}+4{x}-5=0\).
Я найду их устно с помощью теоремы Виета: \( \displaystyle {{x}_{1}}=-5\), \( \displaystyle {{x}_{2}}=1\). Как это делается? Ты можешь научиться этому, прочитав тему «Квадратные уравнения».
Итак, получаем: \( \displaystyle {{x}^{2}}+4{x}-5=\left( x+5 \right)\left( x-1 \right)\), следовательно:
\( \displaystyle y=\frac{x+5}{\left( x+5 \right)\left( x-1 \right)}=\frac{1}{x-1},\text{ }x\ne -5\)Пример 3
Ты уже попробовал решить сам? В чем загвоздка?
Наверняка в том, что в числителе у нас \( \displaystyle 2x\), а в знаменателе – просто \( \displaystyle x\).
Это не беда. Нам нужно будет сократить на \( \displaystyle \left( x+2 \right)\), поэтому в числителе следует вынести \( \displaystyle 2\) за скобки (чтобы в скобках \( \displaystyle x\) получился уже без коэффициента):
\( \displaystyle y=\frac{2{x}-3}{x+1}=\frac{2\left( x-\frac{3}{2} \right)}{x+1}=2\cdot \frac{x-1,5}{x+1}=2\cdot \frac{x+1-1-1,5}{x+1}=…\) дальше сам.
Ответ: \( \displaystyle y=2-\frac{5}{x+1}\).
График обратной пропорциональности
Как всегда, начнем с самого простого случая: \( \displaystyle y=\frac{1}{x}\).
Составим таблицу.
Таблица обратной пропорциональности (зависимости)
| \( \displaystyle \mathbf{x}\) | \( \displaystyle -3\) | \( \displaystyle -2\) | \( \displaystyle -1\) | \( \displaystyle -0,5\) | \( \displaystyle 0,5\) | \( \displaystyle 1\) | \( \displaystyle 2\) | \( \displaystyle 3\) | \( \displaystyle 4\) |
| \( \displaystyle \mathbf{y}\) | \( \displaystyle -\frac{1}{3}\) | \( \displaystyle -\frac{1}{2}\) | \( \displaystyle -1\) | \( \displaystyle -2\) | \( \displaystyle 2\) | \( \displaystyle \;1\) | \( \displaystyle \frac{1}{2}\) | \( \displaystyle \frac{1}{3}\) | \( \displaystyle \frac{1}{4}\) |
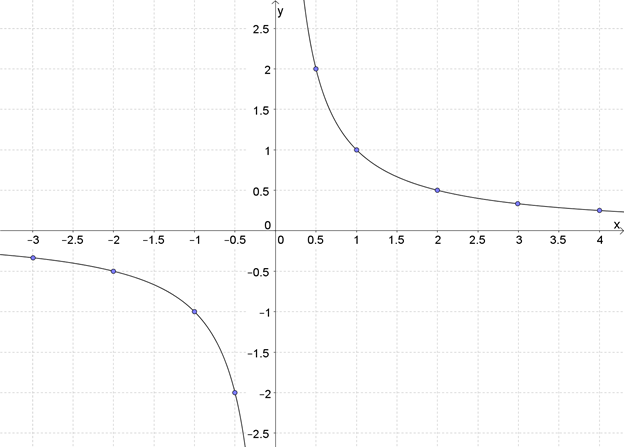
Нарисуем точки на координатной плоскости:
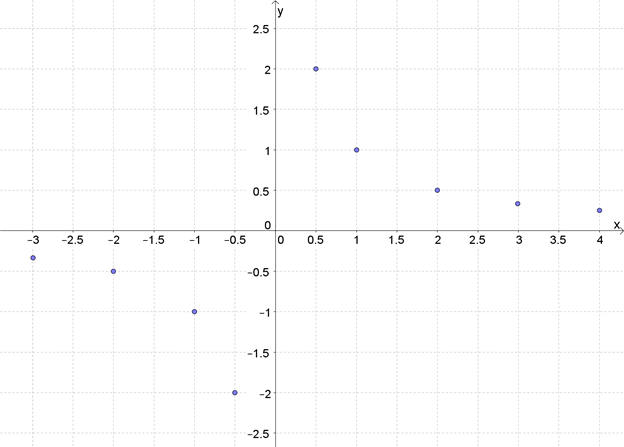
Теперь их надо плавно соединить, но как?
Видно, что точки в правой и левой частях образуют будто бы несвязанные друг с другом кривые линии. Так оно и есть.
Это график гиперболы и выглядит он так:

Этот график называется «гипербола» (есть что-то похожее на «параболу» в этом названии, правда?). Как и у параболы, у гиперболы две ветки, только они не связаны друг с другом.
Каждая из них стремится своими концами приблизиться к осям \( \displaystyle Ox\) и \( \displaystyle Oy\), но никогда их не достигает. Если посмотреть на эту же гиперболу издалека, получится такая картина:
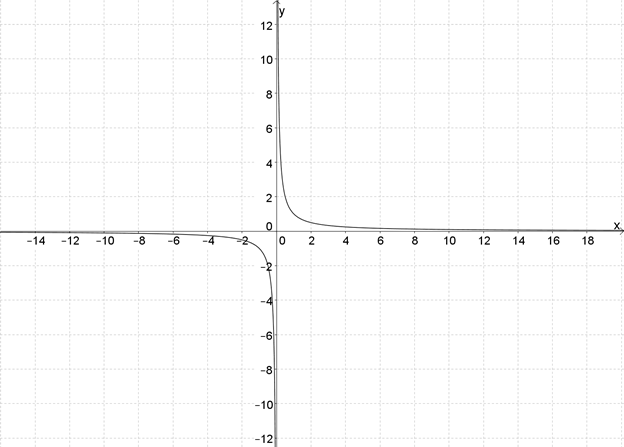
Оно и понятно: так как \( \displaystyle x\ne 0\), график не может пересекать ось \( \displaystyle Oy\). Но и \( \displaystyle y\ne 0\), так что график никогда не коснется и оси \( \displaystyle Ox\).
Ну что же, теперь посмотрим на что влияют коэффициенты.
На что влияют коэффициенты
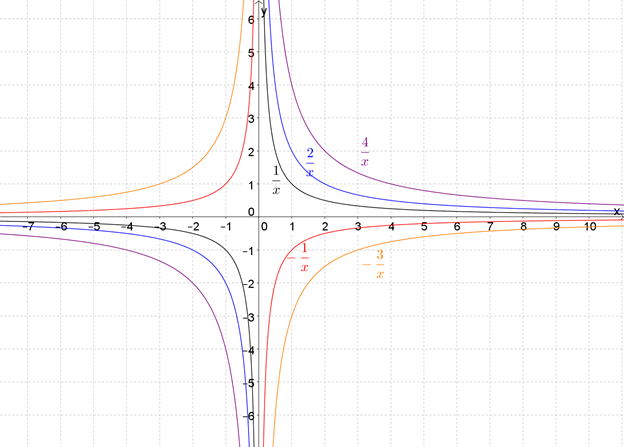
Рассмотрим такие функции:
\( \displaystyle y=\frac{1}{x};\text{ }y=\frac{2}{x};\text{ }y=\frac{4}{x};\text{ }y=-\frac{1}{x};\text{ }y=-\frac{3}{x}\):

Ух ты, какая красота!
Все графики построены разными цветами, чтобы легче было их друг от друга отличать.
Итак, на что обратим внимание в первую очередь?
Например, на то, что если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси \( \displaystyle Ox\).
Второе: чем больше число в знаменателе, тем дальше график «убегает» от начала координат.
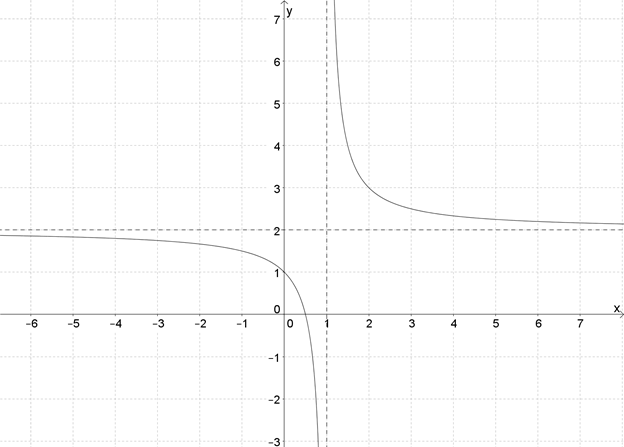
А что, если функция выглядит сложнее, например, \( \displaystyle y=\frac{1}{x-1}+2\)?
В этом случае гипербола будет точно такой же, как обычная \( \displaystyle y=\frac{1}{x}\), только она немного сместится. Давай думать, куда?
Чему теперь не может быть равен \( x\)? Правильно, \( x\ne 1\). Значит, график никогда не достигнет прямой \( x=1\).
А чему не может быть равен \( y\)? Теперь \( y\ne 2\). Значит, теперь график будет стремиться к прямой \( y=2\), но никогда ее не пересечет.
Итак, теперь прямые \( x=1\) и \( y=2\) выполняют ту же роль, которую выполняют координатные оси для функции \( \displaystyle y=\frac{1}{x}\).
Такие прямые называются асимптотами (линии, к которым график стремится, но не достигает их):
Более подробно о том, как строятся такие графики, мы выучим чуть позже.
А теперь попробуй решить несколько примеров для закрепления.
Примеры
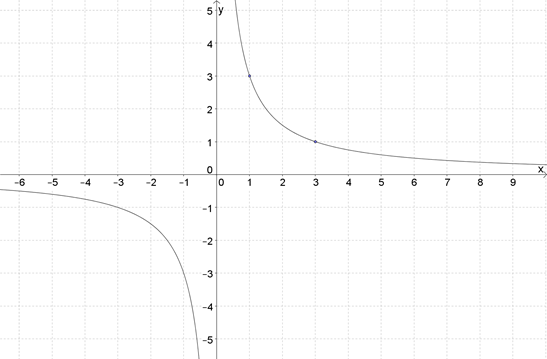
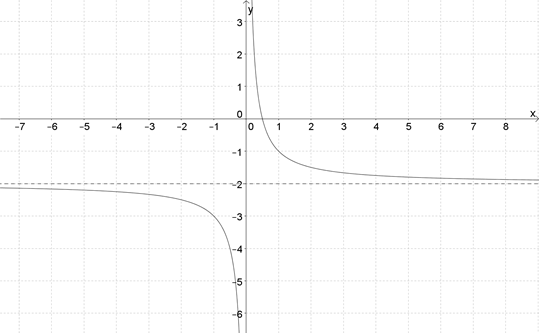
1. На рисунке изображен график функции \( \displaystyle y=\frac{k}{x}\). Определите \( k\).
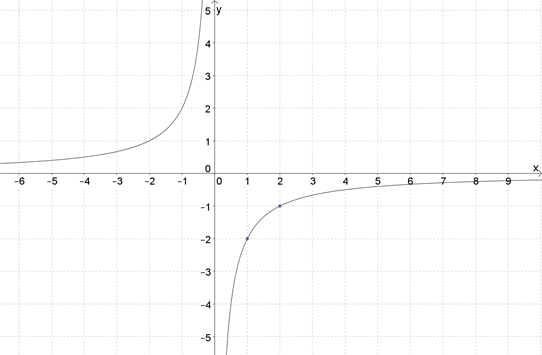
2. На рисунке изображен график функции \( \displaystyle y=\frac{k}{x}\). Определите \( k\)
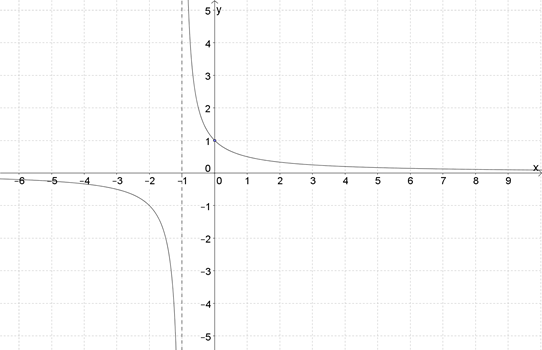
3. На рисунке изображен график функции \( \displaystyle y=\frac{1}{x+a}\). Определите \( a\).
4. На рисунке изображен график функции \( \displaystyle y=\frac{1}{x}+a\). Определите \( a\).
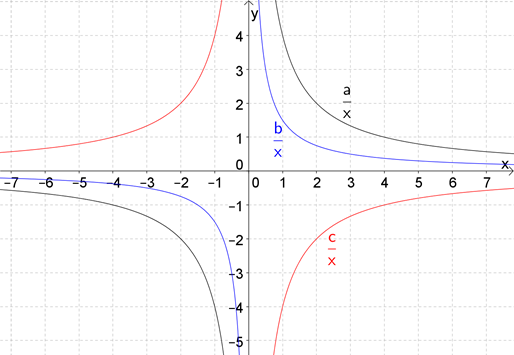
5. На рисунке приведены графики функций \( \displaystyle y=\frac{a}{x},\text{ }y=\frac{b}{x}\) и \( y=\frac{c}{x}\).
Выбери верное соотношение:
a. \( a>b>c\)
b. \( c>a>b\)
c. \( b>c>a\)
d. \( a=c>b\)
Ответы:
- 3
- -2
- 1
- -2
- a
Обратная пропорциональность в жизни
Где же нам встречается такая функция на практике? Примеров множество. Самый распространенный – это движение: чем больше скорость, с которой мы движемся, тем меньшее время нам потребуется, чтобы преодолеть одно и то же расстояние.
И правда, вспомним формулу скорости: \( \displaystyle v=\frac{S}{t}\), где \( v\) – скорость, \( t\) – время в пути, \( S\) – расстояние (путь).
Отсюда можно выразить время: \( \displaystyle t=\frac{S}{v}\)
Пример:
Человек едет на работу со средней скоростью \( 40\) км/ч, и доезжает за \( 1\) час. Сколько минут он потратит на эту же дорогу, если будет ехать со скоростью \( 60\) км/ч?
Решение:
Вообще, такие задачи ты уже решал в 5 и 6 классе. Ты составлял пропорцию:
\( \displaystyle 60\) км/ч – \( 60\) мин.
\( \displaystyle 60\) км/ч – \( x\) мин.
Далее ты определял, что это обратная пропорциональность, так как чем больше скорость, тем меньше время. Значит, чтобы решить эту пропорцию, нужно поделить числа «крест-накрест»:
\( \displaystyle \frac{40}{x}=\frac{60}{60}\text{ }\Rightarrow \text{ }x=40\)(мин).
То есть понятие обратной пропорциональности тебе уже точно знакомо. Вот и вспомнили. А теперь то же самое, только по-взрослому: через функцию.
Функция (то есть зависимость) времени в минутах от скорости:
\( \displaystyle t\left( v \right)=\frac{S}{v}\).
Известно, что \( t\left( 40 \right)=60\), тогда:
\( \frac{S}{40}=60\text{ }\Rightarrow \text{ }S=40\cdot 60=2400\).
Нужно найти \( t\left( 60 \right)\):
\( \displaystyle t\left( 60 \right)=\frac{2400}{60}=40\) (мин).
Теперь придумай сам несколько примеров из жизни, в которых присутствует обратная пропорциональность.
Придумал? Молодец, если да. Удачи!
Принципы построения графика обратной пропорциональности (гиперболы)
Теперь давай научимся строить простейшую гиперболу – \( \displaystyle y=\frac{k}{x}\).
Достаточно помнить, как она выглядит, и тогда нам хватит всего трех-четырех точек.
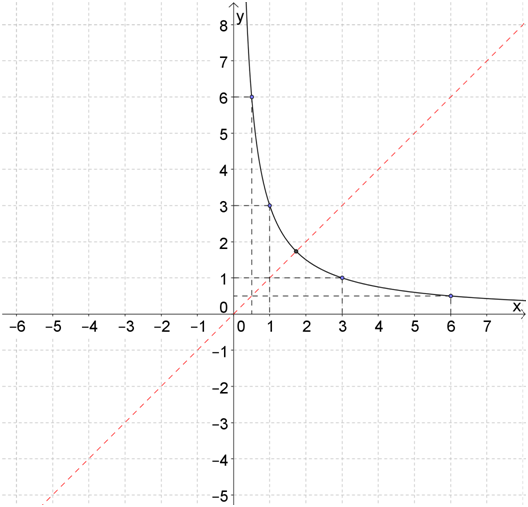
Например, построим гиперболу \( \displaystyle y=\frac{3}{x}\).
Составим таблицу из \( 4\) точек, которые принадлежат одной ветке (например, правой):
| \( x\) | \( \frac{1}{2}\) | \( \displaystyle 1\) | \( \displaystyle 3\) | \( \displaystyle 6\) |
| \( y\) | \( \displaystyle 6\) | \( \displaystyle 3\) | \( \displaystyle 1\) | \( \frac{1}{2}\) |
Отмечаем точки на рисунке:
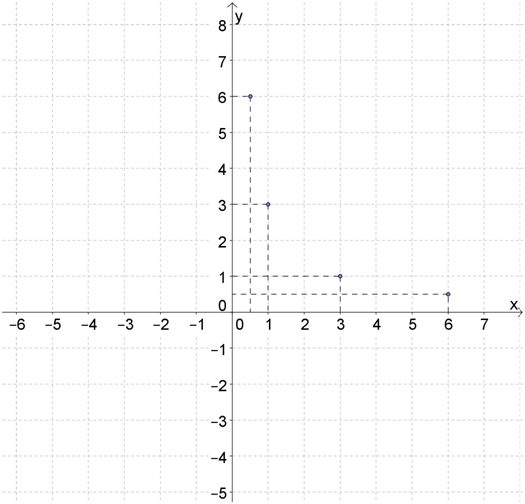
Проводим через них плавную линию, которая краями приближается к осям:
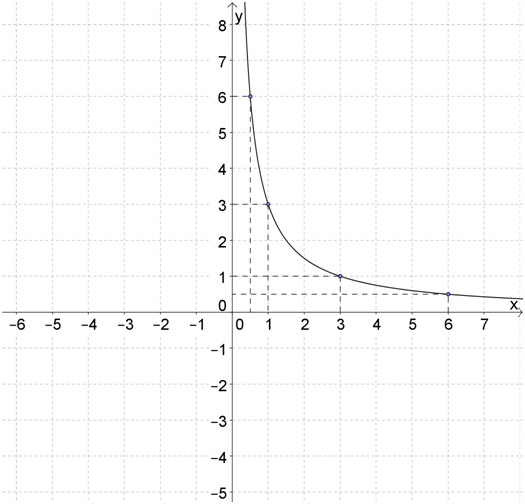
Это одна ветвь гиперболы
Проверить правильность построения этой кривой можно так: она должна быть симметрична относительно биссектрисы угла между осями координат:
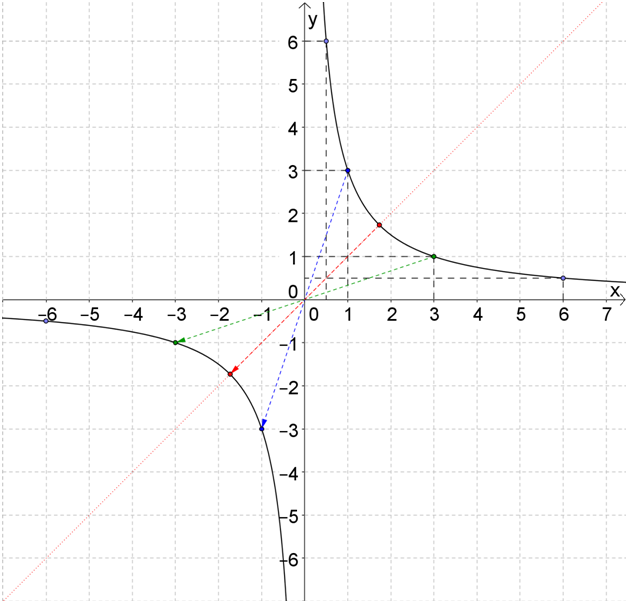
Отлично, осталось вспомнить, что собой представляет вторая ветвь?
Это точно такая же кривая, расположенная симметрично относительно начала координат. То есть как будто оси теперь направлены не снизу вверх и слева направо, а наоборот: сверху вниз и справа налево, и мы рисуем ту же самую ветвь гиперболы.
Вот:
Еще один полезный факт.
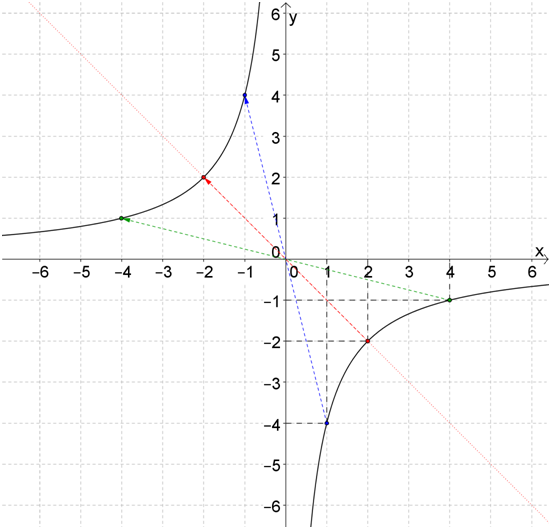
Посмотри на красные точки на графике. Видно, что их абсцисса совпадает с ординатой. Так вот, эти абсцисса с ординатой равны \( \sqrt{k}\) для правой ветви гиперболы, и \( -\sqrt{k}\) для левой.
Для функций, у которых \( k\) – точный квадрат (например, \( 1\), \( 4\) или \( \displaystyle \frac{1}{4}\)), эту точку, относительно которой ветвь гиперболы симметрична, будет очень легко поставить.
В этом случае достаточно даже трех точек, чтобы построить график.
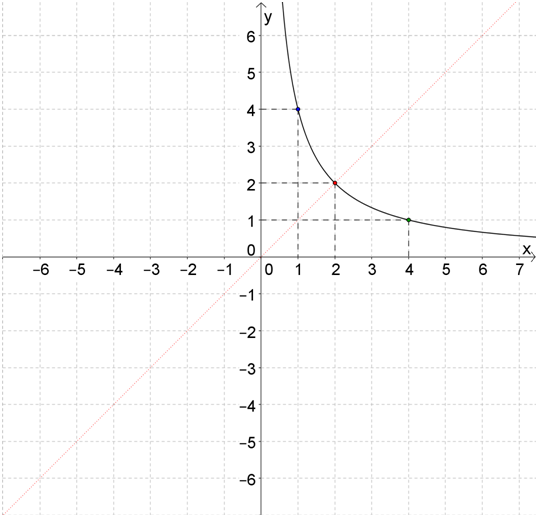
Например, построим график функции \( \displaystyle y=\frac{4}{x}\)
Как и в прошлый раз, начнем с правой ветви.
Точка симметрии: \( \displaystyle x=y=2\). Выберем еще одну точку, например, \( \displaystyle x=1\), \( \displaystyle y=4\). У третьей точки координаты будут наоборот: \( \displaystyle x=4\), \( \displaystyle y=1\).
Рисуем:
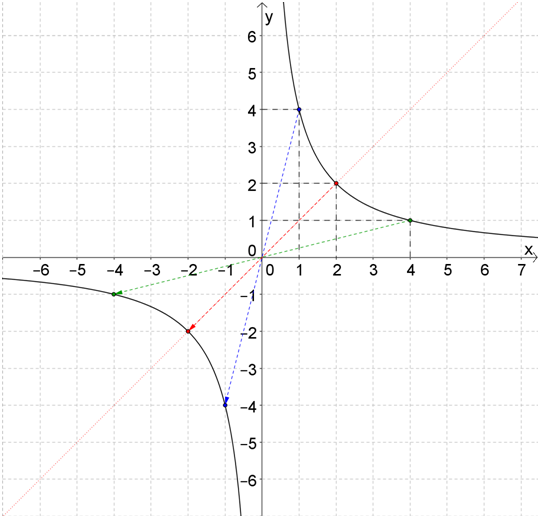
И теперь симметрично отображаем эту ветвь в третью координатную четверть:
Теперь выясним, что будет, если \( \displaystyle k<0\)?
Очень просто: если есть график функции с таким же по величине, но положительным \( \displaystyle k\), то нужно просто отразить его относительно оси \( \displaystyle Ox\)
То есть правая ветвь теперь будет ниже оси \( \displaystyle Ox\) (в \( \displaystyle IV\) четверти), а левая – выше (в \( \displaystyle III\) четверти).
Принцип построения же останется прежним:
Ну что же, осталось объединить все то, что мы уже выяснили в один алгоритм:
Алгоритм построения гиперболы
Алгоритм построения графика функции \( \displaystyle y=\frac{k}{x-a}+b\)
- Определяем коэффициенты \( \displaystyle k\), \( \displaystyle a\) и \( \displaystyle b\).
- Строим график функции \( \displaystyle y=\frac{k}{x}\) (сначала по 3-4 точкам правую ветвь, потом симметрично рисуем левую ветвь).
- График должен быть сдвинут вправо на \( \displaystyle a\). Но проще двигать не график, а оси, так что ось \( \displaystyle Oy\) сдвигаем влево на \( \displaystyle a\).
- График должен быть сдвинут вверх на \( \displaystyle b\). Но проще двигать не график, а оси, так что ось \( \displaystyle Ox\) сдвигаем вниз на \( \displaystyle b\).
- Старые оси (прямые, которые служили нам осями в пункте 2) оставляем в виде пунктирных линий. Это теперь просто вертикальная и горизонтальная асимптоты.
Шесть примеров построения графиков гиперболы
- \( \displaystyle y=\frac{2}{x-1}+1\)
- \( \displaystyle y=\frac{1}{2-x}-1\)
- \( \displaystyle y=\frac{2}{2-3x}+2\)
- \( \displaystyle y=\frac{x-3}{{{x}^{2}}-9}\)
- \( \displaystyle y=1-\frac{2{x}-5}{4{{x}^{2}}-4{x}-15}\)
- \( \displaystyle y=\frac{2{x}-1}{x+3}+1\)
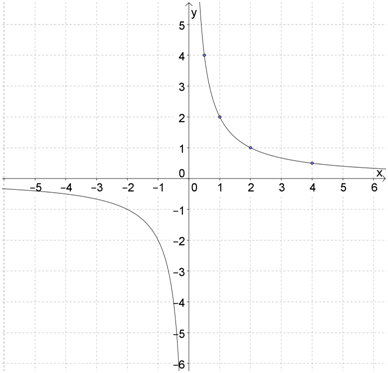
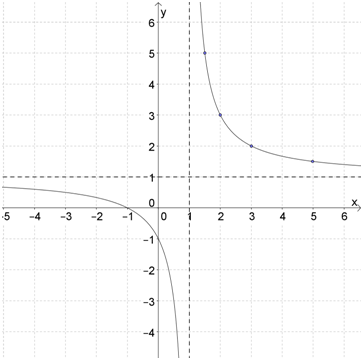
Пример 1. Пойдем по порядку по пунктам.
1) \( \displaystyle k=2\); \( \displaystyle a=1\); \( \displaystyle b=1\)
2) \( \displaystyle y=\frac{2}{x}\):
3), 4) и 5):
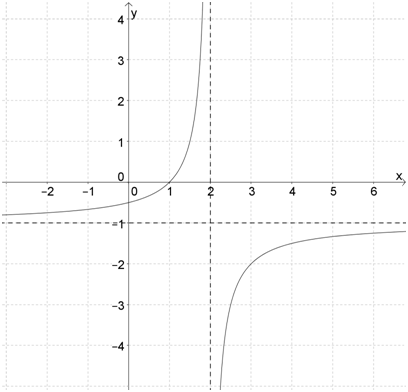
Пример 2. Сначала преобразуем выражение:
\( \displaystyle y=\frac{1}{2-x}-1=\frac{-1}{x-2}-1\).
Теперь ясно, что \( \displaystyle k=-1\); \( \displaystyle a=2\); \( \displaystyle b=-1\):
Пример 3.
\( \displaystyle y=\frac{2}{2-3x}+2=\frac{-2}{3{x}-2}+2=\frac{-2}{3\left( x-\frac{2}{3} \right)}+2=\frac{-\frac{2}{3}}{x-\frac{2}{3}}+2\).
\( \displaystyle k=-\frac{2}{3}\); \( a=\frac{2}{3}\); \( b=2\):
Пример 4.
\( \displaystyle y=\frac{x-3}{{{x}^{2}}-9}=\frac{x-3}{\left( x-3 \right)\left( x+3 \right)}=\frac{1}{x+3},\text{ }x\ne 3\).
\( k=1\), \( a=-3\), \( b=0\). Дополнительное условие \( x\ne 3\) означает, что на графике появится выколотая точка c абсциссой \( x=3\):
Пример 5.
\( \displaystyle y=1-\frac{2{x}-5}{4{{x}^{2}}-4{x}-15}\).
Ты уже, наверное, догадался, что вместо того, чтобы смотреть на эту функцию квадратными глазами и говорить: «Что это?!», нужно просто взять и упростить выражение.
Если не знаешь, как это делать, то тебе прямая дорога в тему «Преобразование выражений».
Итак, если ты уже усвоил тему «Преобразование выражений», то тебе не составит труда упростить нашу функцию. Вот что должно получиться:
\( \displaystyle y=1-\frac{2{x}-5}{4{{x}^{2}}-4{x}-15}=1-\frac{1}{2x+3}=\frac{-\frac{1}{2}}{x+\frac{3}{2}}+1,\text{ }x\ne \frac{5}{2}\).
\( \displaystyle k=-\frac{1}{2}\), \( \displaystyle a=-\frac{3}{2}\), \( b=1\), выколотая точка \( \displaystyle x\ne \frac{5}{2}\):
Пример 6. \( \displaystyle y=\frac{2{x}-1}{x+3}+1\).
Здесь нужно не то чтобы упростить, тут нужно привести выражение к виду обратной зависимости:
\( \displaystyle y=\frac{2{x}-1}{x+3}+1=\frac{2x+6-6-1}{x+3}+1=\frac{2\left( x+3 \right)-7}{x+3}+1=\)
\( \displaystyle =\frac{2\left( x+3 \right)}{x+3}-\frac{7}{x+3}+1=2-\frac{7}{x+3}+1\)
\( \displaystyle y=-\frac{7}{x+3}+3\):
Ну вот и все, ты научился строить любую гиперболу.
Замечу также, что правила построения гиперболы оказались немного проще, чем для параболы, ведь каждое число просто сдвигает график в какую-то одну сторону.
И коэффициенты не связаны друг с другом.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)
Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.
Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики.
На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях).
Мы рассмотрим:
- степенную функцию (линейную, квадратичную, обратную зависимость, корни),
- тригонометрические и обратные тригонометрические,
- показательную и
- логарифмическую функции.
Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
С.М.
01 ноября 2019
Очень красиво излагаете!
Александр (админ)
01 ноября 2019
Спасибо, С.М!
Мария Соколюк
17 декабря 2019
Кратно и доступно.Спасибо.
Александр (админ)
17 декабря 2019
Мария, спасибо большое за отзыв на нашу работу! Удачи!