Решение текстовых задач на ЕГЭ (простейших)
Текстовая задача – это задача №1 на ЕГЭ или так называемая прикладная задача или задача с физическим содержанием.
По названию понятно, что умение решать такие задачи пригодиться в жизни. А еще они очень простые:
- Нужно выделить математическое содержание из словесного описания задачи.
- Исходя из общей, житейской логики, проверить правильность решения.
Давай посмотрим на примерах.
На ЕГЭ есть еще ряд тестовых задач:
Но в этой статье мы научимся решать самые простые текстовые задачи — задачи с физическим содержанием. Мы их называем «чтобы в магазине не обманули». )
Текстовые задачи — коротко о главном
Текстовые задачи (№1 в ЕГЭ) –одни из самых простых в ЕГЭ. Их еще называют задачи с физическим содержанием или прикладные задачи.
Алгоритм решения задач такой:
- Нужно описать математически то, что сказано словами
- Исходя из общей, житейской логики, проверить правильность решения.
Задачи на нахождение оптимального варианта (бывшая В4) – в них требуется найди оптимальный из нескольких вариантов, представленных для выбора.
- Для решения таких задач нужно рассмотреть и просчитать каждый вариант в отдельности.
- Выбрать вариант, отвечающий условию.
Простейшие текстовые задачи
Пример №1
Шоколадка стоит \( \displaystyle 28\) рублей. Какое наибольшее количество шоколадок можно купить на \( \displaystyle 160\) рублей.
Решение:
Всего у нас есть \( \displaystyle 160\) рублей. На \( \displaystyle 28\) рублей можно купить \( \displaystyle 1\) шоколадку. А на \( \displaystyle 160\) рублей: \( \displaystyle \frac{160}{28}=5,714\) шоколадки.
А теперь подумаем, можно ли купить \( \displaystyle 5,714\) шоколадки? Конечно же нет! Можно купить или \( \displaystyle 5\) или \( \displaystyle 6\) шоколадок.
Очевидно, что нам хватит денег только на \( \displaystyle 5\), ведь \( \displaystyle 6\) шоколадок будут стоить — \( \displaystyle 6\cdot 28=168\). А у нас есть только \( \displaystyle 160\).
Ответ: \( \displaystyle 5\).
Это был совсем простой пример. Теперь давай посмотрим более реалистичные задачи.
Пример №2
Булка хлеба стоит \( \displaystyle 20\) рублей. Какое максимальное количество булок хлеба можно купить на \( \displaystyle 150\) рублей, после повышения цены хлеба на \( \displaystyle 10\)%?
Решение:
Сколько мы можем купить хлеба? Наша сумма (\( \displaystyle 150\) рублей), деленная на цену хлеба. Но цена изменилась. Давай найдем новую цену.
Произошло повышение на \( \displaystyle 10\)%. А чему равняется \( \displaystyle 1\) процент от старой цены (\( \displaystyle 20\) рублей)
Процент – это сотая доля числа, а значит \( \displaystyle 1\) процент = \( \displaystyle \frac{20}{100}=0,2\).
А \( \displaystyle 10\) таких процентов? Правильно, десять умножить на \( \displaystyle 1\) процент: \( \displaystyle 0,2\cdot 10=2\).
Значит, цена увеличилась на \( \displaystyle 2\) рубля и стала составлять \( \displaystyle 20+2=22\) рубля.
Теперь находим максимальное количество булок хлеба: \( \displaystyle \frac{150}{22}=6,8181\).
Можно ли купить \( \displaystyle 6,8181\) булок хлеба?
Нет. Или \( \displaystyle 6\) или \( \displaystyle 7\).
Денег на \( \displaystyle 7\) булок нам не хватит (\( \displaystyle 7\cdot 22=154\) рубля). Значит ответ \( \displaystyle 6\).
Ответ: \( \displaystyle 6\).
Если тебе не совсем понятен пункт 1. б) – повтори разделы «Дроби и рациональные числа» и «Проценты«.
Попробуй решить несколько похожих задач самостоятельно. Вполне возможно ты разберешься.
3 примера для самостоятельной работы
- Оптовая цена футболки \( \displaystyle 80\) рублей. Розничная цена на \( \displaystyle 80\)% выше оптовой. Какое наибольшее число футболок можно купить по розничной цене на \( \displaystyle 1500\) рублей?
- Магазин покупает саженцы розы по оптовой цене \( \displaystyle 100\) рублей за штуку и продает с наценкой \( \displaystyle 15\)%. Какое наибольшее количество саженцев можно купить в этом магазине на \( \displaystyle 500\) рублей?
- Футболка стоит \( \displaystyle 200\) руб. Какое наибольшее количество футболок можно купить на \( \displaystyle 1500\) рублей во время распродажи с учетом \( \displaystyle 20\)% скидки.
Ответы:
- \( \displaystyle 10\)
- \( \displaystyle 4\)
- \( \displaystyle 9\)
Хватит покупок. Теперь давай рассмотрим задачи чуть-чуть сложнее.
Более сложные текстовые задачи
Пример №6
Больному ангиной необходимо пить \( \displaystyle 1\) столовую ложку сиропа \( \displaystyle 4\) раза в день. В одной ложке содержится \( \displaystyle 15\) мл лекарства, которое необходимо принимать в течение \( \displaystyle 2\) недель.
Сироп продается в бутылочках по \( \displaystyle 200\) мл. Какого наименьшего количества бутылочек хватит на весь курс лечения?
Решение:
Ух… Сироп, лекарство, бутылочки… С какой стороны подступить… Давай начнем с начала.
Выделяем математическое содержание из словесного описания: «\( \displaystyle 1\) столовая ложка сиропа \( \displaystyle 4\) раза в день». То есть \( \displaystyle 4\) ложки в день. «В одной ложке \( \displaystyle 15\) мл лекарства».
Значит на \( \displaystyle 1\) день нам нужно \( \displaystyle 15\cdot 4=60\) мл лекарства.
«Курс длится \( \displaystyle 2\) недели», или \( \displaystyle 14\) дней. Значит на весь курс нужно \( \displaystyle 60\cdot 14=840\) мл лекарства. Вот теперь уже все ясно. Посчитаем количество бутылочек:
\( \displaystyle \frac{840}{200} = 4,2\)
\( \displaystyle 4\) или \( \displaystyle 5\) бутылочек? Очевидно, что \( \displaystyle 4\) нам не хватит (ведь в них только \( \displaystyle 800\) мл лекарства). Значит нужно покупать \( \displaystyle 5\) бутылочек.
Ответ: \( \displaystyle 5\).
Пример №7
Одного рулона обоев хватает для поклейки полосы от пола до потолка шириной \( \displaystyle 1,2\) м. Сколько нужно рулонов обоев для оклейки прямоугольной комнаты размерами \( \displaystyle 3,6\) м на \( \displaystyle 4,8\) м?
Решение:
1. Одного рулона нам хватит на \( \displaystyle 1,2\) метра. Значит нужно посчитать, сколько таких метров нужно на всю комнату (найти периметр комнаты): \( \displaystyle 3,6\cdot 2+4,8\cdot 2=16,8\) м.
2. А теперь найдем количество рулонов обоев: \( \displaystyle \frac{16,8}{1,2}=14\).
Ответ: \( \displaystyle 14\).
Ну и последний типичный пример.
Пример №8
Алеша вылетает на самолете из Москвы в Пекин в \( \displaystyle 19:20\) и прибывает в \( \displaystyle 3:50\) по московскому времени. Сколько часов длится полет?
Решение:
Простая и житейская задача. А как можно посчитать? Можно воспользоваться двумя самыми простыми способами.
Способ 1
Длительность перелета можно посчитать путем сложения количества часов полета до \( \displaystyle 00:00\) и после \( \displaystyle 00:00\).
Тогда из \( \displaystyle 24\) часов вычтем \( \displaystyle 19\) часов \( \displaystyle 20\) минут и получим \( \displaystyle 4\) часа \( \displaystyle 40\) минут.
т.е. до полуночи полет длился \( \displaystyle 4\) часа \( \displaystyle 40\) минут. После полуночи полет длился \( \displaystyle 3\) часа \( \displaystyle 50\) минут.
Сначала сложим часы \( \displaystyle 4+3=7\) часов.
Затем минуты \( \displaystyle 40+50=90\) минут, что эквивалентно \( \displaystyle 1\) часу и \( \displaystyle 30\) минутам.
\( \displaystyle 7\) часов + \( \displaystyle 1\) час \( \displaystyle 30\) минут = \( \displaystyle 8\) часов \( \displaystyle 30\) минут – длительность перелета из Москвы в Пекин.
Способ 2
Альтернативный вариант.
Изобразим на картинке указанный промежуток полета зеленым цветом.
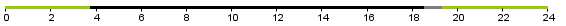
И теперь ясно, что найти искомый промежуток времени можно, если из \( \displaystyle 24\) часов вычесть время вне полета (ту часть временной шкалы, которая закрашена черным).
Найдем это черный промежуток: из \( \displaystyle 19\) часов \( \displaystyle 20\) минут вычтем \( \displaystyle 3\) часа \( \displaystyle 50\) минут и получим \( \displaystyle 15\) часов \( \displaystyle 30\) минут.
Теперь осталось из \( \displaystyle 24\) часов вычесть получившийся результат: \( \displaystyle 24\) часа минус \( \displaystyle 15\) часов \( \displaystyle 30\) минут = \( \displaystyle 8\) часов \( \displaystyle 30\) минут.
При записи ответа нужно помнить, что нас просили дать ответ в часах, а \( \displaystyle 30\) минут – это полчаса, или \( \displaystyle 0,5\) часа, т.е. полет длится \( \displaystyle 8,5\) часов.
Ответ: \( \displaystyle 8,5\)
Попробуй решить несколько задач самостоятельно:
Еще 6 задач на самостоятельную работу
- На кладку тротуаров расходуется \( \displaystyle 350\) плиток в день. В машину, которая поставляет плитки с завода на склад, помещается \( \displaystyle 2800\) плиток. Какое наименьшее число рейсов должна совершить машина, чтобы привезти запас на \( \displaystyle 5\) недель?
- Кекс стоит \( \displaystyle 45\) рублей. В субботу в кондитерской действует специальное предложение: заплатив за \( \displaystyle 2\) кекса, покупатель получает \( \displaystyle 3\) (один в подарок). Сколько кексов можно получить на \( \displaystyle 250\) рублей в субботу?
- Для приготовления малинового морса требуется \( \displaystyle 300\) мл варенья на \( \displaystyle 1,5\) литра кипяченой воды. Какое наименьшее количество полулитровых банок варенья необходимо для приготовления \( \displaystyle 4,5\) литров морса?
- В гимназии «Всезнайка» учится \( \displaystyle 1500\) учеников. Среди них \( \displaystyle 15\)% после окончания гимназии поступают в вузы родного города, а остальные – в вузы других городов. Среди уезжающих выпускников \( \displaystyle 40\)% поступает на технические специальности. Сколько уезжающих выпускников поступает на другие специальности?
- Самолет Москва-Пхукет отправляется в \( \displaystyle 17:40\), а прибывает в \( \displaystyle 3:10\) на следующий день (время московское). Сколько часов самолет находится в пути?
- Одного рулона обоев хватает для поклейки полосы от пола до потолка шириной \( \displaystyle 1,4\) м. Сколько нужно рулонов обоев для оклейки прямоугольной комнаты размерами \( \displaystyle 4,6\) м на \( \displaystyle 5,7\) м?
Ответы:
- \( \displaystyle 5\)
- \( \displaystyle 7\)
- \( \displaystyle 2\)
- \( \displaystyle 765\)
- \( \displaystyle 9,5\)
- \( \displaystyle 15\)
Бонус: задачи по выбору оптимального решения (есть только в ОГЭ и базовом варианте ЕГЭ)
Ранее эта задача называлась B4 . Сейчас она сохранилась только в базовом варианте ЕГЭ и в ОГЭ. Мы ее оставили здесь, потому что на наш взгляд, умение решать эту задачу очень важно для жизни.
Итак, требуется из нескольких вариантов, представленных для выбора, найти оптимальный.
Пример №15
Максим хочет заниматься в тренажерном зале, и у него есть выбор между пакетами услуг, предлагаемыми залом. Максим предполагает, что будет посещать зал \( \displaystyle 14\) раз в месяц. Сколько нужно заплатить Максиму за месяц занятий, если он выбирает самый дешевый вариант?
| Пакет услуг | Месячный абонемент | Плата за каждое отдельное занятие сверх абонемента (руб.) |
| А | нет | 300 |
| Б | 10 занятий за 2800 рублей | 290 |
| В | 15 занятий за 4050 рублей | 280 |
Решение:
Для решения таких задач нужно рассмотреть и просчитать каждый вариант в отдельности, а затем выбрать тот, который отвечает условию (в нашем случае – самый дешевый). Давай считать.
Пакет А. Здесь подразумевается плата за каждое занятие в отдельности. \( \displaystyle 14\) занятий по \( \displaystyle 300\) рублей – это \( \displaystyle 14\cdot 300=4200\) рублей.
Пакет Б. Максим приобретает \( \displaystyle 10\) занятий за \( \displaystyle 2800\) рублей, а оставшиеся \( \displaystyle 14-10=4\) занятия по \( \displaystyle 290\) рублей, т.е. за \( \displaystyle 4\cdot 290=1160\) рублей. Всего в этом случае Максим потратит \( \displaystyle 2800+1160=3960~\) рублей.
Пакет В. Покупается \( \displaystyle 15\) занятий за \( \displaystyle 4050\) рублей. Одно занятие в итоге сгорает.
Посчитав каждый из вариантов мы знаем, что наиболее выгодным для Максима оказался вариант Б, выбрав который, он заплатит \( \displaystyle 3960\) рублей.
Ответ: \( \displaystyle 3960\).
Видишь, ничего сложного!
Давай рассмотрим пример посложнее.
Пример №16
Независимое агенство каждый месяц определяет рейтинг развлекательных журналов на основе следующих показателей:
- I – показатель информативности
- R – количество рекламы
- O – показатель объективности
- K – качество бумаги
Рейтинг рассчитывается по формуле: \( \displaystyle R=30\left( \frac{3I-3R+5O+2K}{4}+1 \right)\).
В таблице представлены показатели четырех журналов.
| Журнал | I | R | O | К |
| А | 3 | 2 | -2 | 3 |
| Б | -1 | 4 | 2 | 2 |
| В | 2 | 1 | -1 | 1 |
| Г | 1 | 0 | 2 | 0 |
Найдите наивысший рейтинг журнала из представленных в таблице.
Решение:
Решение ничем не отличается от предыдущей задачи. Только здесь значения из таблицы нужно подставлять в формулу.
Давай посчитаем рейтинг для журнала А.
\( \displaystyle {{R}_{a}}=30\left( \frac{3\cdot 3-3\cdot 2+5\left( -2 \right)+2\cdot 3}{4}+1 \right)=\)
\( \displaystyle =30\left( \frac{9-6-10+6}{4}+1 \right)=30\left( -0,25+1 \right)=\)
\( \displaystyle =30\cdot 0,75=22,5\)
Для остальных журналов, посчитай значения сам!
Теперь подставим полученные результаты в таблицу и посмотрим, у какого журнала наивысший рейтинг и сколько он составляет.
| Журнал | I | R | O | K | Рейтинг |
| А | 3 | 2 | -2 | 3 | 22,5 |
| Б | -1 | 4 | 2 | 2 | 22,5 |
| В | 2 | 1 | -1 | 1 | 30 |
| Г | 1 | 0 | 2 | 0 | 127,5 |
Теперь ясно, что наивысший рейтинг \( \displaystyle 127,5\) у журнала Г.
Ответ: \( \displaystyle 127,5\).
В задачах варианты могут быть представлены и без таблицы. Давай рассмотрим такой пример.
Пример №17
Семья из трех человек планирует поехать отдыхать из Москвы в Крым (Симферополь). Можно полететь самолетом, а можно – на своей машине. Билет на самолет на одного человека стоит \( \displaystyle 4500\) рублей туда и обратно.
Автомобиль расходует \( \displaystyle 10\) литров бензина на \( \displaystyle 100\) км, а цена бензина – \( \displaystyle 32,5\) рубля за \( \displaystyle 1\) литр. Расстояние от Москвы до Симферополя – \( \displaystyle 1800\) км.
Сколько рублей придется заплатить за самую дешевую поездку на троих туда и обратно?
Решение:
Здесь нужно рассмотреть каждый вариант в отдельности и выбрать самый дешевый – прям как в задачах с таблицами!
Давай считать:
Полет на самолете. Тут все просто: \( \displaystyle 3\) человека по \( \displaystyle 4500\) рублей – это \( \displaystyle 13500\) рублей.
Поездка на машине. Туда и обратно – это \( \displaystyle 1800+1800=3600\) километров. Машина расходует \( \displaystyle 10\) литров на \( \displaystyle 100\) километров, или \( \displaystyle 100\) литров на \( \displaystyle 1000\) километров.
А у нас \( \displaystyle 3,6\) тысяч километров, а значит \( \displaystyle 100\) литров умножаем на \( \displaystyle 3,6\) – \( \displaystyle 360\) литров бензина. Именно столько нам нужно, чтобы совершить поездку. Один литр стоит \( \displaystyle 32,5\) рублей, а значит общая стоимость поездки будет:
\( \displaystyle 360\cdot 32,5=11700\) рублей.
На машине ехать дешевле!
Ответ: \( \displaystyle 11700\).
Задачи для самостоятельного решения.
Решай и сверяй с ответами!
Пример 18
Мобильный оператор предлагает три тарифных плана интернет-услуг, представленных в таблице.
| Тарифный план | «Ноль» | «1000» | «Безлимит» |
| Абонентская плата (руб.) | нет | 200 | 500 |
| Плата за трафик | 0,7 рублей за 1 Mb | 0,5 рублей за 1 Mb сверх 1000 Mb | нет |
Пользователь планирует, что его трафик не будет превышать \( \displaystyle 1500\) Mb.
Сколько рублей в месяц будет тратить пользователь, если выберет самый выгодный тарифный план?
Пример 19
Строительной фирме нужно приобрести \( \displaystyle 90\) кубометров строительного бруса у одного из трех поставщиков. Определите наименьшую стоимость покупки вместе с доставкой (в рублях). Цена и условия доставки приведены в таблице.
| Поставщик | А | Б | В |
| Цена бруса (руб. за м3) | 1600 | 1700 | 1800 |
| Стоимость доставки (руб.) | 15000 | 6000 | 8000 |
| Дополнительные условия | — | При заказе на сумму свыше 150 000 руб. – доставка бесплатно | При заказе на сумму свыше 170 000 руб. – доставка бесплатно |
Пример 20
Для строительства дома можно использовать один из двух типов фундамента: бетонный и пеноблочный.
Для фундамента из пеноблоков нужно \( \displaystyle 5\) кубометров пеноблоков и \( \displaystyle 2\) мешка цемента.
Для бетонного фундамента необходимо \( \displaystyle 3\) тонны щебня и \( \displaystyle 35\) мешков цемента.
Кубометр пеноблоков стоит \( \displaystyle 2500\) рублей, щебень стоит \( \displaystyle 1000\) рублей за тонну, а мешок цемента – \( \displaystyle 300\) рублей.
Сколько рублей понадобится на покупку материала, если выбирается самый дешевый вариант?
Пример 21
На игровом сервере ведется рейтинг игроков на основе следующих показателей:
- W – процент побед
- K – количество боев
- A – точность стрельбы
- L – уровень персонажа
Рейтинг считается по формуле: \( \displaystyle R=\frac{K}{100L}+100W+50A\).
В таблице представлены показатели 4 игроков.
| Журнал | А | Б | В | Г |
| W | 0,6 | 0,52 | 0,55 | 0,49 |
| K | 100 | 100 | 400 | 3000 |
| A | 0,4 | 0,51 | 0,55 | 0,45 |
| L | 7 | 2 | 4 | 11 |
Найдите наивысший рейтинг, среди игроков, представленных в таблице.
Ответы:
- \( \displaystyle 450\)
- \( \displaystyle 153000\)
- \( \displaystyle 13100\)
- \( \displaystyle 83,5\)
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org


