Объемы фигур (ЕГЭ 2022)
Так же, как у плоских фигур есть такая характеристика, как площадь, у объемных тел есть… объем.
И так же, как рассуждения о площади начинаются с квадрата (1×1), рассуждения об объеме начинаются с куба (1x1x1).
Читай эту статью и научишься находить объемы различных фигур!
Объемы фигур — коротко о главном
Объем куба
\( \displaystyle V=abc\)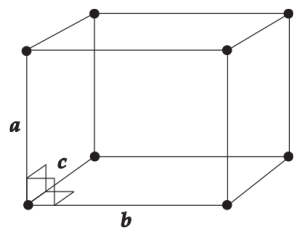
Объем призмы
\( \displaystyle V={{S}_{\text{основания}}}\ \ \ \ \cdot \text{H}\)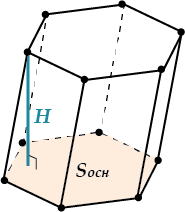
Объем пирамиды
\( \displaystyle V=\frac{1}{3}{{S}_{\text{основания}}}\ \ \ \ \ \cdot \text{H}\)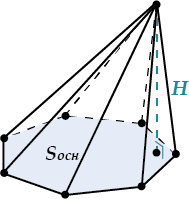
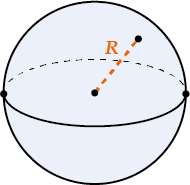
Объем шара
\( \displaystyle {{V}_{\text{шара}}}\ \ \ \ \ =\frac{4}{3}\pi {{R}^{3}}\)\( R\) – радиус
Объем цилиндра
\( V=\pi {{R}^{2}}H\)\( R\) – радиус основания
\( H\) – высота
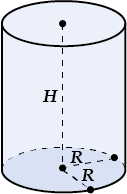
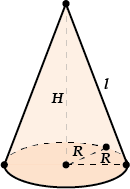
Объем конуса
\( V=\frac{1}{3}\pi {{R}^{2}}H\)\( R\) – радиус основания
\( H\) – высота
Объем куба
Как было сказано выше, рассуждения об объеме начинаются с куба \( \displaystyle 1х1х1\).
Объем куба с ребром \( \displaystyle \text{1}\) метр равен \( \displaystyle \text{1}\) кубическому метру.
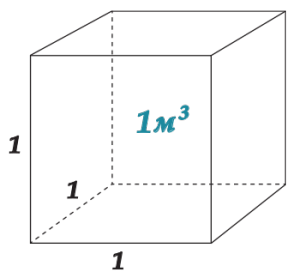
Помнишь, квадратный метр – это была площадь квадрата \( \displaystyle 1х1\) и обозначалась она \( \displaystyle \text{1}\) м.кв.
Ну вот, а объем куба с ребром \( \displaystyle \text{1}\) называется кубическим метром и обозначается \( \displaystyle \text{1}\) м.кв.
Что же такое \( \displaystyle \text{2}\) м.кв.? А вот, смотри:
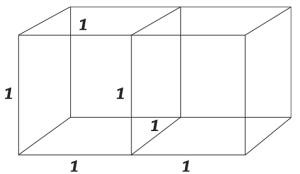
Это два кубика с ребром \( \displaystyle \text{1}\).
А чему равен объем куба с ребром \( \displaystyle \text{2}\)?
Давай считать:
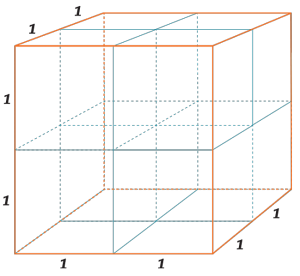
Сколько в большом кубе (с ребром \( \displaystyle \text{2}\)) маленьких (с ребром \( \displaystyle \text{1}\))?
Конечно, \( \displaystyle \text{8}\). Поэтому объем куба с ребром \( \displaystyle \text{2}\) равен \( \displaystyle \text{8}\) кубическим метрам, то есть \( \displaystyle \text{8}\) м.кв.
А ведь \( \displaystyle \text{8}\) это \( \displaystyle \text{23}\).
И представь себе, это для любого куба, даже с ребром \( \displaystyle \sqrt{239}\) верна формула.
\( \displaystyle V\)куба\( \displaystyle={{a}^{3}}\)
Эту формулу легко доказать для целых a (мы уже видели доказательство для \( \displaystyle a=2\)), чуть сложнее – для рациональных и совсем сложно для иррациональных \( \displaystyle a\).
Но мы пойдем дальше.
Подобным же образом получается формула объема для прямоугольного параллелепипеда.
Объем прямоугольного параллелепипеда

\( \displaystyle V=abc\)
Звучит это так:
Объем прямоугольного параллелепипеда равен произведению его измерений – длины, ширины и высоты.
А дальше… начинается множество формул.
Объем призмы
Главная формула объема призмы
\( \displaystyle V={{S}_{\text{основания}}}\ \ \ \ \cdot \text{H}\)
\( \displaystyle {{S}_{\text{основания}}}\ \ \ \ \) –площадь основания
\( H\) – высота

Эта формула объема призмы верна для любой призмы, но если призма прямая, то \( H\) «превращается» в боковое ребро. И тогда
\( \displaystyle V={{S}_{\text{основания}}}\ \ \ \ \cdot \text{H}\) – то же самое, что
\( \displaystyle V=S{{\ }_{основания}}\ \ \ \cdot боковое\ ребро\)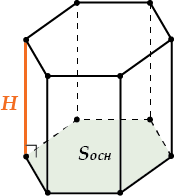
Необычная формула объема призмы
Представь себе, есть ещё одна, «перевёрнутая» формула для объёма призмы.
\( \Large \text{V}={{\text{S}}_{\bot }}\cdot l\)
\( {{\text{S}}_{\bot }}\) – площадь сечения, перпендикулярного боковому ребру,
\( l\) – длина бокового ребра.
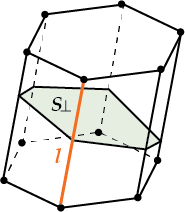
Используется ли эта формула в задачах? Честно говоря, довольно редко, так что можешь ограничиться знанием основной формулы объёма.
Объем пирамиды
Главная формула объема пирамиды
\( \displaystyle \Large V=\frac{1}{3}{{S}_{осн}}\cdot H\)
Откуда взялась именно \( \displaystyle \frac{1}{3}\)? Это не так уж просто, и на первых порах нужно просто запомнить, что у пирамиды и конуса в формуле объема есть \( \displaystyle \frac{1}{3}\), а у пирамиды и цилиндра – нет.
Теперь давай посчитаем объем самых популярных пирамид.
Объем правильной треугольной пирамиды
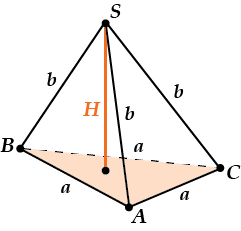
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\). Нужно найти \( \displaystyle {{S}_{осн}}\) и \( \displaystyle H\).
\( \displaystyle {{S}_{осн}}\) – это площадь правильного треугольника \( \displaystyle ABC\).
Вспомним, как искать эту площадь. Используем формулу площади:
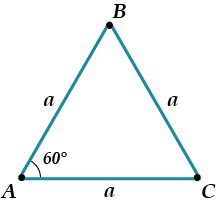
\( \displaystyle S=\frac{1}{2}ab\cdot \sin \gamma \).
У нас «\( \displaystyle a\)» – это \( \displaystyle a\), а «\( \displaystyle b\)» — это тоже \( \displaystyle a\), а \( \displaystyle \sin \gamma =\sin 60{}^\circ =\frac{\sqrt{3}}{2}\).
Значит, \( \displaystyle {{S}_{ABC}}=\frac{1}{2}{{a}^{2}}\frac{\sqrt{3}}{2}=\frac{{{a}^{2}}\sqrt{3}}{4}\).
Теперь найдем \( \displaystyle H\).
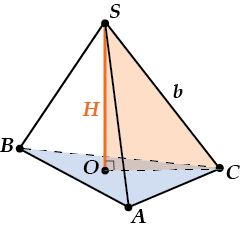
По теореме Пифагора для \( \displaystyle \Delta SOC\)
\( \displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}\).
Чему же равно \( \displaystyle OC\)? Это радиус описанной окружности в \( \displaystyle \Delta ABC\), потому что пирамидаправильная и, значит, \( \displaystyle O\) — центр \( \displaystyle \Delta ABC\).
Найдем \( \displaystyle OC\) (Подробнее смотри в теме «Правильный треугольник»).
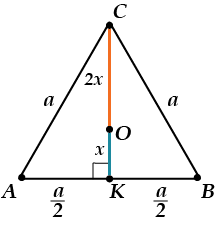
\( \displaystyle OC=\frac{2}{3}CK\), так как \( \displaystyle O\) — точка пересечения и медиан тоже.
\( \displaystyle C{{K}^{2}}=A{{C}^{2}}-A{{K}^{2}}\) (теорема Пифагора для \( \displaystyle \Delta ACK\))
\( \displaystyle C{{K}^{2}}-{{a}^{2}}-\frac{{{a}^{2}}}{4}=\frac{3{{a}^{2}}}{4}\); \( \displaystyle CK=\frac{a\sqrt{3}}{2}\)
Значит, \( \displaystyle OC=\frac{2}{3}\cdot \frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}\)
Подставим \( \displaystyle OC\) в формулу для \( \displaystyle H\).
\( \displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}={{b}^{2}}-{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}={{b}^{2}}-\frac{{{a}^{2}}}{3}\)
И подставим все в формулу объема:
\( \displaystyle V=\frac{1}{3}{{S}_{ABC}}\cdot H=\frac{1}{3}\cdot \frac{{{a}^{2}}\sqrt{3}}{4}\cdot \sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{3}}\)
\( \displaystyle V=\frac{{{a}^{2}}\sqrt{3}}{12}\sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{3}}\).
Внимание: если у тебя правильный тетраэдр (т.е. \( \displaystyle b=a\)), то формула получается такой:
\( \displaystyle V=\frac{{{a}^{3}}}{6\sqrt{2}}\).
Объем правильной четырехугольной пирамиды
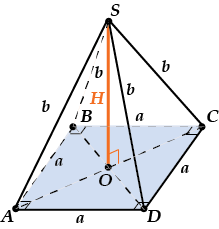
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\).
\( \displaystyle V=\frac{1}{3}{{S}_{OCH}}H\).
Здесь \( \displaystyle {{S}_{OCH}}\) и искать не нужно; ведь в основании – квадрат, и поэтому \( \displaystyle {{S}_{OCH}}={{a}^{2}}\).
Найдем \( \displaystyle H\). По теореме Пифагора для \( \displaystyle \Delta SOD\)
\( \displaystyle {{H}^{2}}={{b}^{2}}-O{{D}^{2}}\).
Известно ли нам \( \displaystyle OD\)?
Ну, почти. Смотри:
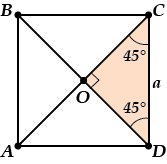
\( \displaystyle OD=a\cdot \cos 45{}^\circ =\frac{a}{\sqrt{2}}\) (это мы увидели, рассмотрев \( \displaystyle \Delta COD\)).
Подставляем \( \displaystyle OD\) в формулу для \( \displaystyle H\):
\( \displaystyle {{H}^{2}}={{b}^{2}}-\frac{{{a}^{2}}}{2}\);
\( \displaystyle H=\sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{2}}\)
А теперь и \( \displaystyle H\) и \( \displaystyle {{S}_{OCH}}\) подставляем в формулу объема.
\( \displaystyle V=\frac{1}{3}{{S}_{OCH}}\cdot H=\frac{1}{3}{{a}^{2}}\sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{2}}\).
Объем правильной шестиугольной пирамиды
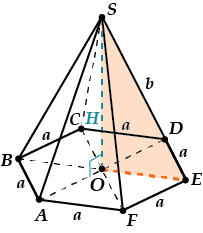
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро \( \displaystyle b\).
\( \displaystyle V=\frac{1}{3}{{S}_{OCH}}\cdot H\).
Как найти \( \displaystyle {{S}_{OCH}}\)? Смотри, шестиугольник \( \displaystyle ABCDEF\) состоит ровно из шести одинаковых правильных треугольников. Площадь правильного треугольника мы уже искали при подсчете объема правильной треугольной пирамиды, здесь используем найденную формулу.
\( \displaystyle {{S}_{ABCDEF}}=6\cdot {{S}_{AOF}}=6\cdot \frac{{{a}^{2}}\sqrt{3}}{4}=\frac{3\sqrt{3}{{a}^{2}}}{2}\)
Теперь найдем \( \displaystyle H\) (это \( \displaystyle SO\)).
По теореме Пифагора для \( \displaystyle \Delta SOE\)
\( \displaystyle {{H}^{2}}={{b}^{2}}-OE\)?
Но чему же равно \( \displaystyle OE\)? Это просто \( \displaystyle a\), потому что \( \displaystyle \Delta EOF\) (и все остальные тоже) правильный.
Значит,
\( \displaystyle {{H}^{2}}={{b}^{2}}-{{a}^{2}}\)
\( \displaystyle H=\sqrt{{{b}^{2}}-{{a}^{2}}}\)
Подставляем:
\( \displaystyle V=\frac{1}{3}{{S}_{OSN}}\cdot H=\frac{1}{3}\cdot \frac{3\sqrt{3}{{a}^{2}}}{2}\cdot \sqrt{{{b}^{2}}-{{a}^{2}}}\)
\( \displaystyle V=\frac{\sqrt{3}}{2}{{a}^{2}}\sqrt{{{b}^{2}}-{{a}^{2}}}\)
Тела вращения
Еще о телах вращения здесь.
Объем шара
\( \displaystyle {{V}_{\text{шара}}}\ \ \ \ \ =\frac{4}{3}\pi {{R}^{3}}\)\( R\) — радиус

Это еще одна хитрая формула, которую придется запомнить, не понимая, откуда она взялась.
Однажды сможешь доказать ее сам!
Объем цилиндра
\( V=\pi {{R}^{2}}H\)\( R\) – радиус основания
\( H\) – высота

Объем конуса
\( V=\frac{1}{3}\pi {{R}^{2}}H\)\( R\) – радиус основания
\( H\) – высота

Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №14 по профильной математике. Стереометрия
Для того, чтобы решать успешно ЕГЭ №14 по профильной математике, нужно великолепно знать основные теоремы планиметрии, уметь рассчитывать расстояния, площади и объемы плоских и объемных фигур.
Но самое сложное, нужно научиться строить доказательства с помощью этих теорем и правильно их записывать.
ЕГЭ №8. Расстояния и углы в пространстве на примере куба, параллелепипеда и призмы
Итак, задание №8 из профильного ЕГЭ.
Задачи на нахождение расстояний и углов в пространстве в объемных фигурах (куб, параллелепипед, призма) и комбинированных фигурах.
Вы также можете посмотреть разбор всех остальных задач из первой части профильного ЕГЭ.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org


