Сравнение чисел при решении уравнений, неравенств и задач с модулями
При решении уравнений и неравенств, а также задач с модулями требуется расположить найденные корни на числовой прямой.
Как ты знаешь, найденные корни могут быть разными.
Они могут быть такими: \( 4\), \( -3\), \( 8\), \( 125\).
А могут быть и вот такими: \( \sqrt{6}\), \( \left( 4-\sqrt{3} \right)\), \( \frac{\sqrt[6]{6}}{\sqrt{13}+\frac{4}{13}}\).
Если числа не рациональные, а иррациональные, или представляют собой сложные математические выражения, то расположить их на числовой прямой весьма проблематично.
Для этого нужно уметь их сравнивать.
Калькуляторами на экзамене пользоваться нельзя, а приближенный подсчет не дает 100% гарантий, что одно число меньше другого (вдруг разница между сравниваемыми числами \( 0,000001\)?).
Что делать?
Прочитай эту статью и все поймешь!
Конечно, ты знаешь, что положительные цифры всегда больше отрицательных, и что если мы представим числовую ось, то при сравнении, наибольшие числа будут находиться правее, чем наименьшие: \( 3>1\); \( -1>-3\); \( 0>-3\) и т.д.
Но всегда ли все так легко? Где на числовой оси мы отметим \( \sqrt{6}\), \( \left( 4-\sqrt{3} \right)\), \( \frac{\sqrt[6]{6}}{\sqrt{13}+\frac{4}{13}}\).
Как их сравнить, например, с числом \( 5\)? Вот в этом-то и загвоздка … )
Для начала поговорим в общих чертах как и что сравнивать.
Если надо сравнить числа \( a\) и \( b\), между ними ставим знак \( \vee \) (происходит от латинского слова Versus или сокращенно vs. – против): \( a\vee b\).
Этот знак заменяет неизвестный нам знак неравенства (\( >\text{ или }<\)).
Далее будем выполнять тождественные преобразования до тех пор, пока не станет ясно, какой именно знак нужно поставить между числами.
Суть сравнения чисел состоит в следующем:
Мы относимся к знаку \( \vee \) так, будто это какой-то знак неравенства.
И с выражением \( a\vee b\) мы можем делать все то же, что делаем обычно с неравенствами.
5 основных преобразований, применяемых при сравнении чисел
- Прибавить любое число к обеим частям (и вычесть, конечно, тоже можем)
- «Перенести все в одну сторону», то есть вычесть из обеих частей одно из сравниваемых выражений. На месте вычитаемого выражения останется 0
- Домножать или делить на одно и то же число. Если это число отрицательное, знак неравенства меняется на противоположный
- Возводить обе части в одну и ту же степень. Если эта степень – четная, необходимо убедиться, что обе части имеют одинаковый знак; если обе части положительны, при возведении в степень знак не меняется, а если отрицательны, тогда меняется на противоположный
- Извлечь корень одинаковой степени из обеих частей. Если извлекаем корень четной степени, необходимо предварительно убедиться, что оба выражения неотрицательны
- Любые другие равносильные преобразования
Важно: преобразования желательно делать такими, чтобы знак неравенства не менялся!
То есть…
В ходе преобразований нежелательно домножать на отрицательное число, и нельзя возводить в квадрат, если одна из частей отрицательна.
5 вариантов сравнения дробей
- Приведение к общему знаменателю
- Приведение к общему числителю
- Вычитание одной дроби из другой
- Приведение к виду десятичной дроби
- Деление одной дроби на другую
Например, нам необходимо сравнить две дроби: \( 1,6\) и \( 1\frac{6}{13}\).
Давай разберем каждый вариант
Вариант 1. Сравнение дробей с помощью приведения к общему знаменателю
Запишем \( 1,6\) в виде обыкновенной дроби:
\( 1,6=1\frac{6}{10}=1\frac{3}{5}\) — (как ты видишь, я также сократила на \( 2\) числитель и знаменатель).
Теперь нам необходимо сравнить дроби:
\( 1\frac{3}{5}\) и \( 1\frac{6}{13}\)
Сейчас мы можем продолжить сравнивать также двумя способами. Мы можем:
Способ 1. Числитель больше знаменателя
Просто приведите все к общему знаменателю, представив обе дроби как неправильные (числитель больше знаменателя):
\( \frac{8}{5}\vee \frac{19}{13}\)
\( \frac{8\cdot 13}{5\cdot 13}\vee \frac{19\cdot 5}{13\cdot 5}\)
\( \frac{104}{65}\vee \frac{95}{65}\)
Какое число больше? Правильно, то, у которого числитель больше, то есть первое.
Способ 2. Отбросьте единицу
«Отбросьте» \( 1\) (считай, что мы из каждой дроби вычли единицу, и соотношение дробей друг с другом, соответственно, не изменилось) и будем сравнивать дроби:
\( \frac{3}{5}\vee \frac{6}{13}\)
Приводим их также к общему знаменателю:
\( \frac{3\cdot 13}{13\cdot 5}\vee \frac{6\cdot 5}{13\cdot 5}\)
Заметь, в принципе мы можем не считать знаменатель. Мы итак видим, что он одинаков и нам необходимо сравнивать числитель. Тогда зачем мы будем тратить время на подсчет знаменателя?
\( \frac{39}{13\cdot 5}\vee \frac{30}{13\cdot 5}\)
Мы получили абсолютно точно такой же результат, как и в предыдущем случае – первое число больше, чем второе:
\( 1,6>1\frac{6}{13}\)
Проверим также, правомерно ли мы вычли единицу? Посчитаем разницу в числителе при первом расчете и втором:
1) \( 104-95=9\)
2) \( 39-30=9\)
Итак, мы рассмотрели, как сравнивать дроби, приводя их к общему знаменателю. Перейдем к другому методу – сравнение дробей приводя их к общему… числителю.
Вариант 2. Сравнение дробей с помощью приведения к общему числителю
Да, да. Это не опечатка. В школе редко кому рассказывают этот метод, но очень часто он весьма удобен. Чтобы ты быстро понял его суть, задам тебе только один вопрос – «в каких случаях значение дроби наибольшее?»
Конечно, ты скажешь «когда числитель максимально большой, а знаменатель максимально маленький».
Например, ты же точно скажешь, что \( \frac{8}{13}<\frac{12}{13}\) Верно?
А если нам надо сравнить такие дроби: \( \frac{6}{13}\vee \frac{6}{28}\)?
Думаю, ты тоже сразу верно поставишь знак, ведь в первом случае \( 6\) делят на \( 13\) частей, а во втором на целых \( 28\), значит, во втором случае кусочки получаются совсем маленькие, и соответственно: \( \frac{6}{13}>\frac{6}{28}\).
Как ты видишь, знаменатели здесь разные, а вот числители одинаковы. Однако, для того, чтобы сравнить эти две дроби, тебе не обязательно искать общий знаменатель. Хотя… найди его и посмотри, вдруг знак сравнения все же неправильный?
\( \frac{6\cdot 28}{13\cdot 28}>\frac{6\cdot 13}{28\cdot 13}\)
\( \frac{168}{364}>\frac{78}{364}\)
А знак-то тот же.
Вернемся к нашему изначальному заданию – сравнить \( 1\frac{3}{5}\)и \( 1\frac{6}{13}\). Будем сравнивать \( \frac{3}{5}\) и \( \frac{6}{13}\).
Приведем данные дроби не к общему знаменателю, а к общему числителю.
Для этого просто числитель и знаменатель первой дроби умножим на \( 2\). Получим:
\( \frac{6}{10}\) и \( \frac{6}{13}\).
Какая дробь больше? Правильно, первая.
Вариант 3. Сравнение дробей с помощью вычитания
Как сравнивать дроби с помощью вычитания? Да очень просто.
Мы из одной дроби вычитаем другую. Если результат получается положительным, то первая дробь (уменьшаемое) больше второй (вычитаемое), а если отрицательным, то наоборот.
В нашем случае попробуем из второй вычесть первую дробь: \( 1\frac{6}{13}-1,6\).
Как ты уже понял, мы так же переводим \( 1,6\) в обыкновенную дробь и получаем тот же результат — \( 1\frac{3}{5}\) .
Наше выражение приобретает вид:
\( 1\frac{6}{13}-1\frac{3}{5}\)
Далее нам все равно придется прибегнуть к приведению к общему знаменателю.
Вопрос как: первым способом, преобразуя дроби в неправильные, или вторым, как бы «убирая» единицу? Кстати, это действие имеет вполне математическое обоснование. Смотри:
\( \left( 1+\frac{6}{13} \right)-\left( 1+\frac{3}{5} \right)=1+\frac{6}{13}-1-\frac{3}{5}=\frac{6}{13}-\frac{3}{5}\)
Мне больше нравится второй вариант, так как перемножение в числителе при приведении к общему знаменателю становится в разы проще.
Приводим к общему знаменателю:
\( \frac{6}{13}-\frac{3}{5}=\frac{6\cdot 5}{13\cdot 5}-\frac{3\cdot 13}{5\cdot 13}=\frac{30}{13\cdot 5}-\frac{39}{5\cdot 13}=-\frac{9}{5\cdot 13}\)
Здесь главное не запутаться, какое число и откуда мы отнимали. Внимательно посмотреть ход решения и случайно не перепутать знаки. Мы отнимали от второго числа первое и получили отрицательный ответ, значит?..
Правильно, первое число больше второго.
\( 1,6>1\frac{6}{13}\)Вариант 4. Сравнение дробей с помощью приведения к виду десятичной дроби
Разобрался в предыдущем примере? А теперь попробуй сравнить дроби:
\( 1,5\vee 1\frac{3}{5}\)
Стоп, стоп. Не спеши приводить к общему знаменателю или вычитать.
Посмотри: \( 1\frac{3}{5}\) можно легко перевести в десятичную дробь. Сколько это будет? Правильно. Что в итоге больше?
\( 1,5<1,6\)
Это еще один вариант – сравнение дробей путем приведения к десятичной дроби.
Вариант 5. Сравнение дробей с помощью деления
Да, да. И так тоже можно.
Логика проста: когда мы делим большее число на меньшее, в ответе у нас получается число, больше единицы, а если мы делим меньшее число на большее, то ответ приходится на промежуток от \( 0\) до \( 1\).
Чтобы запомнить это правило, возьми для сравнения любые два простых числа, например, \( 6\) и \( 4\). Ты же знаешь, что \( 6\) больше \( 4\)?
Теперь разделим \( 6\) на \( 4\). Наш ответ — \( 1,5\). Соответственно, теория верна.
Если мы разделим \( \displaystyle 4\) на \( 6\), что мы получим \( 0,\left( 6 \right)\) – меньше единицы, что в свою очередь подтверждает, что \( \displaystyle 4\) на самом деле меньше \( 6\).
Попробуем применить это правило на обыкновенных дробях. Сравним:
\( \frac{6}{8}\vee \frac{10}{12}\)
Разделим первую дробь на вторую:
\( \frac{6}{8}:\frac{10}{12}=\frac{6}{8}\cdot \frac{12}{10}\)
Сократим на \( 2\) и на \( 4\).
\( \frac{6}{8}\cdot \frac{12}{10}=\frac{3}{2}\cdot \frac{3}{5}=\frac{9}{10}\)
Полученный результат меньше \( 1\), значит делимое меньше делителя, то есть:
Мы разобрали все возможные варианты сравнения дробей. Как мы и говорили их пять.
Готов тренироваться? Сравни дроби оптимальным способом.
Сравним ответы:
Сравнение степеней
Теперь представим, что нам необходимо сравнить не просто числа, а выражения, где существует степень (читай раздел про степени).
Cравни: \( {{2}^{4}}\vee {{2}^{6}}\).
Конечно, ты без труда поставишь знак:
\( {{2}^{4}}<{{2}^{6}}\), ведь если мы заменим степень умножением, мы получим:
\( 2\cdot 2\cdot 2\cdot 2<2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\)
Из этого маленького и примитивного примера вытекает правило:
Если основание сравниваемых степеней одинаково, то больше та степень, у которой больше показатель степени.
Попробуй теперь сравнить следующее: \( {{5}^{4}}\vee {{6}^{4}}\). Ты так же без труда поставишь знак:
\( {{5}^{4}}<{{6}^{4}}\), потому что, если мы заменим возведение степень на умножение…
В общем, ты все понял, и это совсем несложно.
Сложности возникают только тогда, когда при сравнении у степеней разные и основания, и показатели.
В этом случае необходимо попробовать привести к общему основанию. Например:
\( {{2}^{2}}\vee {{4}^{3}}\)
Разумеется, ты знаешь, что \( 4\) это \( {{2}^{2}}\), соответственно, выражение приобретает вид:
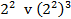
Раскроем скобки и сравним то, что получится:
\( {{2}^{2}}\vee {{2}^{6}}\) — легко?
\( {{2}^{2}}<{{2}^{6}}\)Несколько особый случай, когда основание степени (\( a\)) меньше единицы.
Если \( 0<a<1\), то из двух степеней \( {{a}^{m}}\) и \( {{a}^{n}}\) больше та, показатель которой меньше.
Попробуем доказать это правило.
Пусть \( m>n\).
Введем некоторое натуральное число \( k\), как разницу между \( m\) и \( n\).
Тогда \( m=n+k\).
Поэтому:
\( {{a}^{m}}={{a}^{n+k}}\)
Логично, неправда ли?
\( {{a}^{n+k}}={{a}^{n}}\cdot {{a}^{k}}\)
А теперь еще раз обратим внимание на условие — \( 0<a<1\).
Соответственно: \( 0<{{a}^{k}}<1\). Следовательно, \( {{a}^{m}}={{a}^{n+k}}={{a}^{n}}\cdot {{a}^{k}}<{{a}^{n}}\).
Например:
\( {{\left( \frac{2}{7} \right)}^{42}}>{{\left( \frac{2}{7} \right)}^{142}}\)Как ты понял, мы рассмотрели случай, когда основания степеней равны.
Теперь посмотрим, когда основание находится в промежутке от \( 0\) до \( 1\), но равны показатели степени. Здесь все очень просто.
Запомним, как это сравнивать на примере:
\( {{\left( \frac{1}{3} \right)}^{2}}\vee {{\left( \frac{1}{4} \right)}^{2}}\)
Конечно, ты быстро посчитал:
\( \frac{1}{9}>\frac{1}{16}\)
Поэтому, когда тебе будут попадаться похожие задачи для сравнения, держи в голове какой-нибудь простой аналогичный пример, который ты можешь быстро просчитать, и на основе этого примера проставляй знаки в более сложном.
Выполняя преобразования, помни, что если ты домножаешь, складываешь, вычитаешь или делишь, то все действия необходимо делать и с левой и с правой частью (если ты умножаешь на \( 2\), то умножать необходимо и то, и другое).
Кроме этого, бывают случаи, когда делать какие-либо манипуляции просто невыгодно. Например, тебе нужно сравнить \( {{5}^{2}}\vee {{4}^{3}}\). В данном случае, не так сложно возвести в степень, и расставить знак исходя из этого:
\( {{5}^{2}}\vee {{4}^{3}}\)
\( 25<64\)
Давай потренируемся. Сравни степени:
Готов сравнивать ответы? Вот что у меня получилось:
Возведение в степень
Пример:
Что больше: \( \displaystyle \sqrt{2}\) или \( \displaystyle 1,4\)?
Решение:
Поскольку обе части неравенства положительны, можем возвести в квадрат, чтобы избавиться от корня:
\( \displaystyle \sqrt{2}\text{ }\vee \text{ }1,4\text{ }\Leftrightarrow \text{ }{{\left( \sqrt{2} \right)}^{2}}\vee {{\left( 1,4 \right)}^{2}}\text{ }\Leftrightarrow \text{ }2\overset{>}{\mathop{\vee }}\,1,96\text{ }\Rightarrow \text{ }\sqrt{2}>1,4\text{ }\).
Пример:
Что больше: \( \displaystyle \sqrt{3}\) или \( \displaystyle \sqrt[3]{5}\)?
Решение:
Здесь тоже можем возвести в квадрат, но это нам поможет избавиться только от квадратного корня. Здесь надо возводить в такую степень, чтобы оба корня исчезли. Значит, показатель этой степени должен делиться и на \( 2\) (степень первого корня), и на \( 3\).
Таким числом является \( 6\), значит, возводим в \( 6\) -ю степень:
\( \displaystyle \sqrt{3}\vee \sqrt[3]{5}\text{ }\Leftrightarrow \text{ }{{\left( \sqrt{3} \right)}^{6}}\vee {{\left( \sqrt[3]{5} \right)}^{6}}\text{ }\Leftrightarrow \text{ }{{3}^{3}}\vee {{5}^{2}}\text{ }\Leftrightarrow \text{ }27\overset{>}{\mathop{\vee }}\,25\text{ }\Rightarrow \text{ }\sqrt{3}>\sqrt[3]{5}\text{ }\).
Сравнение чисел с корнем
Для начала вспомним, что такое корни? Вот эту \( \sqrt[n]{a}=b\) запись помнишь?
\( \sqrt[n]{a}=b\ \ \ \ \ \ \ {{b}^{n}}=a\)Корнем \( n-ой\) степени из действительного числа \( a\) называется такое число \( b\), для которого выполняется равенство \( {{b}^{n}}=a\).
Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.
Значением корня часто является бесконечная десятичная дробь, что затрудняет его точное вычисление, поэтому важно уметь сравнивать корни.
Если ты подзабыл, что это такое и с чем его едят – почитай про корни здесь. Если все помнишь – давай учиться поэтапно сравнивать корни.
Допустим, нам необходимо сравнить:
\( \sqrt[3]{4}\vee \sqrt[3]{6}\)
Чтобы сравнить эти два корня, не нужно делать никаких вычислений, просто проанализируй само понятие «корень».
Понял, о чем я говорю?
Да вот об этом: \( \sqrt[3]{4}\vee \sqrt[3]{6}\)иначе можно записать как третья степень какого-то числа, равна подкоренному выражению.
\( {{x}^{3}}=4\)
\( {{y}^{3}}=6\)
А что больше? \( y\) или \( x\)? Это ты, конечно, сравнишь без всякого труда. Чем большее число мы возводим в степень, тем больше будет значение.
Итак. Выведем правило.
Если показатели степени корней одинаковы (в нашем случае это \( 3\)), то необходимо сравнивать подкоренные выражения (\( 4\) и \( 6\)) — чем больше подкоренное число, тем больше значение корня при равных показателях.
Сложно запомнить? Тогда просто держи в голове пример \( \sqrt{16}\) и \( \sqrt{4}\). Что больше?
\( \sqrt{16}=4\)
\( \sqrt{4}=2\)
\( 4\) больше \( 2\).
Показатели степени корней одинаковы, так как корень квадратный. Подкоренное выражение одного числа (\( 16\)) больше другого (\( 4\)), значит, правило действительно верное.
А что, если подкоренные выражения одинаковые, а вот степени корней разные? Например: \( \sqrt[4]{6}\vee \sqrt[3]{6}\).
Тоже вполне понятно, что при извлечении корня большей степени получится меньшее число. Возьмем для примера:
\( \sqrt[3]{12}\vee \sqrt[6]{12}\)
Обозначим значение первого корня как \( a\), а второго — как \( b\), то:
\( {{a}^{3}}=12\)
\( {{b}^{6}}=12\)
Ты без труда видишь, что в данных уравнениях \( a\) должно быть больше \( b\), следовательно:
\( \sqrt[3]{12}>\sqrt[6]{12}\).
Если подкоренные выражения одинаковы (в нашем случае \( 12\)), а показатели степени корней различны (в нашем случае это \( 3\) и \( 6\)), то необходимо сравнивать показатели степени (\( 3\) и \( 6\)) — чем больше показатель, тем меньше данное выражение.
Попробуй сравнить следующие корни:
Сравним полученные результаты?
С этим благополучно разобрались :). Возникает другой вопрос: а что если у нас все разное? И степень, и подкоренное выражение?
Не все так сложно нам нужно всего- навсего… «избавиться» от корня. Да, да. Именно избавиться)
Если у нас различные и степени и подкоренные выражения, необходимо найти наименьшее общее кратное (читай раздел про целые числа) для показателей корней и возвести оба выражения в степень, равную наименьшему общему кратному.
Что мы все на словах и на словах. Приведем пример:
\( \sqrt[3]{3}\vee \sqrt[2]{5}\)Сравнение логарифмов
Вот так, медленно, но верно, мы подошли к вопросу как же сравнивать логарифмы. Если ты не помнишь что это за зверь такой, советую для начала прочитать теорию из раздела логарифмы.
Прочитал? Тогда ответь на несколько важных вопросов:
- Что называется аргументом логарифма, а что его основанием?
- От чего зависит, возрастает ли функция или убывает?
Если все помнишь и отлично усвоил – приступаем!
Для того, чтобы сравнивать логарифмы между собой, необходимо знать всего 3 приема.
3 приема сравнения логарифмов
- Приведение к одинаковому основанию
- Приведение к одинаковому аргументу
- Сравнение с третьим числом
Изначально, обрати внимание на основание логарифма. Ты помнишь, что:
Если основание логарифма меньше \( 1\), то функция убывает, а если больше, то возрастает.
Именно на этом будет основаны наши суждения. Рассмотрим сравнение логарифмов, которые уже приведены к одинаковому основанию, либо аргументу.
Для начала упростим задачу: пусть в сравниваемых логарифмах равные основания.
Тогда:
Функция \( y={{\log }_{a}}x\), при \( a>0\) возрастает на промежутке от \( \left( 0;\ +\infty \right)\), значит по определению \( {{x}_{1}}<{{x}_{2}}\), то \( {{y}_{1}}<{{y}_{2}}\) («прямое сравнение»)
Пример: \( {{\log }_{3}}6\vee {{\log }_{3}}\frac{18}{21}\) — основания одинаковы, \( a>0\) ,соответственно сравниваем аргументы: \( 6>\frac{18}{21}\), следовательно: \( {{\log }_{3}}6>{{\log }_{3}}\frac{18}{21}\)
Функция \( y={{\log }_{a}}x\), при \( 0<a<1\), убывает на промежутке от \( \left( 0;\ +\infty \right)\), значит по определению \( {{x}_{1}}<{{x}_{2}}\), то \( {{y}_{1}}>{{y}_{2}}\) («обратное сравнение»).\( {{\log }_{\frac{1}{3}}}12\vee {{\log }_{\frac{1}{3}}}24\) — основания одинаковы.
\( 0<a<1\), соответственно сравниваем аргументы: \( 12<24\). Однако, знак у логарифмов будет «обратный», так как функция убывает: \( {{\log }_{\frac{1}{3}}}12>{{\log }_{\frac{1}{3}}}24\).
Теперь рассмотрим случаи, когда основания различны, но одинаковы аргументы.
1. Основание \( a\) больше \( 1\).
\( x>1\). В этом случае используем «обратное сравнение».
Например:\( {{\log }_{3}}12\vee {{\log }_{63}}12\) – аргументы одинаковы, \( a>1\) и \( x>1\).
Сравниваем основания: \( 3<63\) однако, знак у логарифмов будет «обратный»: \( {{\log }_{3}}12>{{\log }_{63}}12\)
\( 0<x<1\). В этом случае используем «прямое сравнение».
Например: \( {{\log }_{3}}\frac{1}{6}\vee {{\log }_{4}}\frac{1}{6}\)
\( 3<4\)
\( {{\log }_{3}}\frac{1}{6}<{{\log }_{4}}\frac{1}{6}\)
2. Основание \( a\) находится в промежутке \( 0<a<1\). \( x>1\). В этом случае используем «прямое сравнение».
Например: \( {{\log }_{\frac{3}{4}}}12\vee {{\log }_{\frac{3}{7}}}12\)
\( \frac{3}{4}>\frac{3}{7}\)
\( {{\log }_{\frac{3}{4}}}12>{{\log }_{\frac{3}{7}}}12\)
\( 0<x<1\). В этом случае используем «обратное сравнение».
Например: \( {{\log }_{\frac{3}{4}}}\frac{13}{14}\vee {{\log }_{\frac{3}{7}}}\frac{12}{17}\)
\( \frac{13}{14}>\frac{12}{17}\) \( {{\log }_{\frac{3}{4}}}\frac{13}{14}<{{\log }_{\frac{3}{7}}}\frac{12}{17}\)Запишем все в общем табличном виде:
| \( a>1\), при этом \( {{a}_{1}}<{{a}_{2}}\) | \( 0<a<1\), при этом \( {{a}_{1}}>{{a}_{2}}\) |
| \( x>1\) | \( {{\log }_{{{a}_{1}}}}x>{{\log }_{{{a}_{2}}}}x\) |
| \( 0<x<1\) | \( {{\log }_{{{a}_{1}}}}x<{{\log }_{{{a}_{2}}}}x\) |
Соответственно, как ты уже понял, при сравнении логарифмов нам необходимо привести к одинаковому основанию, либо аргументу.
К одинаковому основанию мы приходим, используя формулу перехода от одного основания к другому.
Можно также сравнивать логарифмы с третьим числом и на основании этого делать вывод о том, что меньше, а что больше.
Например, подумай, как сравнить вот эти два логарифма?
\( {{\log }_{3}}5\vee {{\log }_{8}}26\)
Небольшая подсказка – для сравнения тебе очень поможет логарифм, аргумент которого будет равен \( 25\).
Подумал? Давай решать вместе.
Мы легко сравним с тобой эти два логарифма:
\( {{\log }_{8}}26\vee {{\log }_{8}}25\)
Не знаешь как? Смотри выше. Мы только что это разбирали. Какой знак там будет? Правильно:
\( {{\log }_{8}}26\vee {{\log }_{8}}25\)
\( {{\log }_{3}}5={{\log }_{9}}25\). Согласен?
Сравним между собой:
\( {{\log }_{8}}25\vee {{\log }_{9}}25\)
У тебя должно получиться следующее:
\( {{\log }_{8}}25>{{\log }_{9}}25\)
А теперь соедини все наши выводы в один. Получилось?
Как избавляться от логарифмов
Как избавляться от логарифмов, подробно описано в теме «Логарифмические неравенства». Основные правила такие:
\({\log _a}x \vee b{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee {a^b}\;{\rm{при}}\;a > 1}\\{x \wedge {a^b}\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \) или \( {\log _a}x \vee {\log _a}y{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee y\;{\rm{при}}\;a > 1}\\{x \wedge y\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \)
Также можем добавить правило про логарифмы с разными основаниями и одинаковым аргументом:
\( \displaystyle \begin{array}{l}a>b>1\ \ \Leftrightarrow \ \ {{\log }_{a}}x<{{\log }_{b}}x\\1>a>b>0\ \ \Leftrightarrow \ \ {{\log }_{a}}x>{{\log }_{b}}x\end{array}\)
Объяснить его можно так: чем больше основание, тем в меньшую степень его придется возвести, чтобы получить один и тот же \( x\). Если же основание меньше \( 1\), то все наоборот, так как соответствующая функция монотонно убывающая.
Пример.
Сравните числа: \( {{\log }_{3}}5\) и \( {{\log }_{8}}26\).
Решение:
Согласно вышеописанным правилам:
\( \displaystyle \left. \begin{array}{l}{{\log }_{8}}26>{{\log }_{8}}25\\{{\log }_{8}}25>{{\log }_{9}}25={{\log }_{3}}5\text{ }\end{array} \right|\Rightarrow \text{ }{{\log }_{8}}26>{{\log }_{3}}5\)
А теперь формула для продвинутых.
Правило сравнения логарифмов можно записать и короче:
\( \displaystyle {{\log }_{a}}x-{{\log }_{a}}y\vee 0\text{ }\Leftrightarrow \text{ }\left( a-1 \right)\left( x-y \right)\vee 0\)Пример:
Что больше: \( \displaystyle \log _{0,3}^{2}\sqrt{5}\) или \( \displaystyle \log _{0,3}^{2}0,45\)?
Решение:
\( \displaystyle \begin{array}{l}\log _{0,3}^{2}\sqrt{5}\vee \log _{0,3}^{2}0,45\text{ }\Leftrightarrow \text{ }\log _{0,3}^{2}\sqrt{5}-\log _{0,3}^{2}0,45\vee 0\text{ }\Leftrightarrow \\\left( {{\log }_{0,3}}\sqrt{5}-{{\log }_{0,3}}0,45 \right)\left( {{\log }_{0,3}}\sqrt{5}+{{\log }_{0,3}}0,45 \right)\vee 0\text{ }\Leftrightarrow \\\left( {{\log }_{0,3}}\sqrt{5}-{{\log }_{0,3}}0,45 \right)\left( {{\log }_{0,3}}\sqrt{5}-{{\log }_{0,3}}{{0,45}^{-1}} \right)\vee 0\text{ }\Leftrightarrow \text{ }\\\underbrace{\underbrace{\left( 0,3-1 \right)}_{<0}\underbrace{\left( \sqrt{5}-0,45 \right)}_{>0}\underbrace{\left( 0,3-1 \right)}_{<0}}_{>0}\left( \sqrt{5}-\frac{20}{9} \right)\vee 0\text{ }\Leftrightarrow \\\left( \sqrt{5}-\frac{20}{9} \right)\vee 0\text{ }\Leftrightarrow \text{ }\sqrt{5}\vee \frac{20}{9}\text{ }\Leftrightarrow \text{ }5\vee \frac{400}{81}\text{ }\Leftrightarrow \text{ }\frac{400}{80}\overset{>}{\mathop{\vee }}\,\frac{400}{81}\text{ }\Rightarrow \\\Rightarrow \text{ }\underline{\underline{\log _{0,3}^{2}\sqrt{5}>\log _{0,3}^{2}0,45}}\end{array}\)Пример:
Сравните, какое из чисел больше: \( \displaystyle \log _{6}^{2}13\text{ }\vee \text{ }2,25\).
Решение:
\( \displaystyle \begin{array}{l}\log _{6}^{2}14\vee 2,25\text{ }\Leftrightarrow \text{ }\log _{6}^{2}14-{{1,5}^{2}}\vee 0\text{ }\Leftrightarrow \text{ }\\\Leftrightarrow \left( {{\log }_{6}}14-{{\log }_{6}}{{6}^{1,5}} \right)\underbrace{\left( {{\log }_{6}}14+{{\log }_{6}}{{6}^{1,5}} \right)}_{>0}\vee 0\text{ }\Leftrightarrow \\\left( 6-1 \right)\left( 14-{{6}^{\frac{3}{2}}} \right)\vee 0\text{ }\Leftrightarrow \text{ }14\vee \sqrt{{{6}^{3}}}\text{ }\Leftrightarrow \text{ }194\overset{<}{\mathop{\vee }}\,216\text{ }\Rightarrow \\\Rightarrow \text{ }\underline{\underline{\log _{6}^{2}14<2,25}}\end{array}\)Сравнение тригонометрических выражений
Что такое синус, косинус, тангенс, котангенс? Для чего нужна единичная тригонометрическая окружность и как на ней найти значение тригонометрических функций?
Если ты не знаешь ответы на эти вопросы, очень рекомендую тебе прочитать теорию по этой теме. А если знаешь, то сравнить тригонометрические выражения между собой для тебя не составляет труда!
Немного освежим память.
Нарисуем единичную тригонометрическую окружность и вписанный в нее треугольник. Справился?
Теперь отметь, по какой стороне у нас откладывается косинус, а по какой синус, используя стороны треугольника. (ты, конечно помнишь, что синус, это отношение противолежащей стороны к гипотенузе, а косинус прилежащей?). Нарисовал? Отлично!
Последний штрих – проставь, где у нас будет \( 0{}^\circ \) , где \( 90{}^\circ \)и так далее. Проставил? Фух)
Сравниваем, что получилось у меня и у тебя.
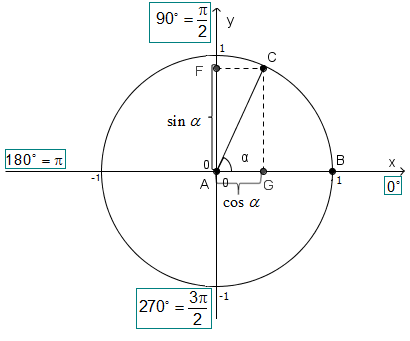
Фух! А теперь приступаем к сравнению!
Допустим, нам необходимо сравнить \( \sin 30{}^\circ \) и \( \sin 60{}^\circ \).
Нарисуй эти углы, используя подсказки в рамочках (где у нас отмечено \( \sin 0{}^\circ \), где \( \sin 90{}^\circ \)), откладывая точки на единичной окружности.
Справился? Вот что у меня получилось.
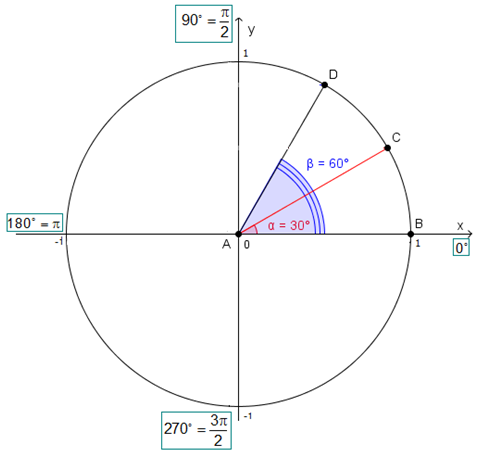
Теперь опустим перпендикуляр из точек, отмеченных нами на окружности на ось… Какую? Какая ось у нас показывает значение синусов? Правильно, \( Oy\).
Вот что у тебя должно получиться:
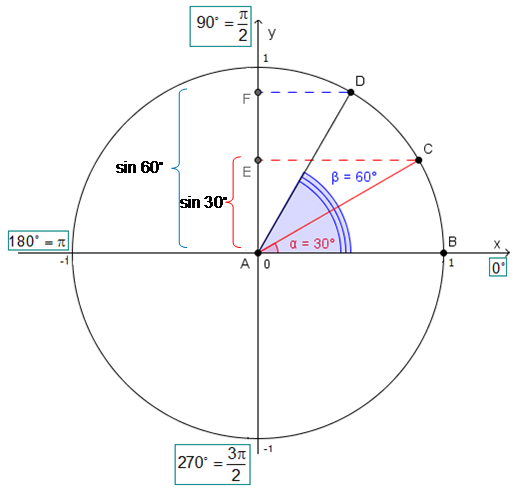
Глядя на этот рисунок, что больше: \( \sin 30{}^\circ \) или \( \sin 60{}^\circ \)?
Конечно, \( \sin 60{}^\circ \), ведь точка \( F\) находится выше точки \( E\).
\( \sin 30{}^\circ <\sin 60{}^\circ \)
Аналогичным образом мы сравниваем значение косинусов. Только перпендикуляр мы опускаем на ось… Верно, \( Ox\).
Соответственно, смотрим, какая точка находится правее (ну или выше, как в случае с синусами), то значение и больше.
Наверное, ты уже догадываешься, как сравнивать тангенсы, верно? Все, что нужно, знать что такое тангенс.
Так что такое тангенс? Правильно, отношение синуса к косинусу.
Чтобы сравнить тангенсы мы так же рисуем угол, как и в предыдущем случае. Допустим, нам необходимо сравнить:
\( tg\ 30{}^\circ \vee tg\ 60{}^\circ \)
Нарисовал? Теперь так же отмечаем значения синуса на координатной оси \( Oy\). Отметил?
А теперь укажи значения косинуса на координатной прямой \( Ox\). Получилось? Давай сравним:
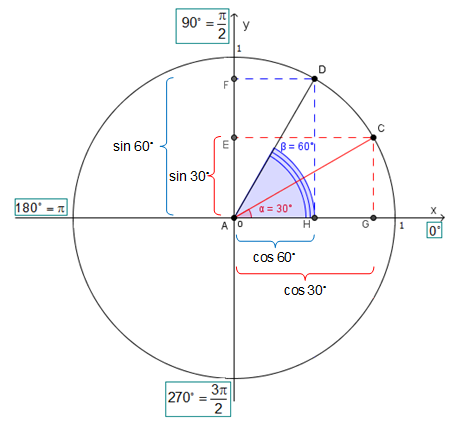
Как ты думаешь, что будет дальше?
Распишем по отрезкам, что такое \( tg\ {{30}^{{}^\circ }}\) и \( tg\ {{30}^{{}^\circ }}\)
\( tg\ {{30}^{{}^\circ }}=\frac{AE}{AG}\)
\( tg\ {{60}^{{}^\circ }}=\frac{AF}{AH}\)
А теперь проанализируй написанное. \( tg\ {{60}^{{}^\circ }}\) — мы большой отрезок делим на маленький. В ответе будет значение, которое точно больше единицы. Верно?
А при \( tg\ {{30}^{{}^\circ }}\) мы маленький делим на большой. В ответе будет число, которое точно меньше единицы.
Так значение какого тригонометрического выражения больше?
Правильно:
\( tg\ {{30}^{{}^\circ }} < tg\ {{60}^{{}^\circ }}\)
Как ты теперь понимаешь, сравнение котангенсов – то же самое, только наоборот: мы смотрим, как относятся друг к другу отрезки, определяющие косинус и синус.
Попробуй самостоятельно сравнить следующие тригонометрические выражения:
Ответы:
Сравните числа с третьим числом
Если \( \displaystyle a>c\) и \( \displaystyle c>b\), то \( \displaystyle a>b\) (закон транзитивности).
Пример 1:
Сравните \( \displaystyle {{15}^{10}}\vee {{9}^{14}}\).
Пример 2:
Что больше: \( \displaystyle lo{{g}_{2}}3\) или \( \displaystyle lo{{g}_{3}}5\)?
Решения:
Умножение на сопряженное
Сопряженным называется множитель, дополняющий выражение до формулы разности квадратов: \( \displaystyle \left( a-b \right)\) – сопряженное для \( \displaystyle \left( a+b \right)\) и наоборот, т.к. \( \displaystyle \left( a-b \right)\left( a+b \right)={{a}^{2}}-{{b}^{2}}\).
Пример:
Что больше: \( \displaystyle \sqrt{8}-\sqrt{7}\) или \( \displaystyle \sqrt{11}-\sqrt{10}\)?
Решение:
Домножим и разделим каждую разность на сопряженную сумму:
Подготовка к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



В разделе сравнения чисел, возведённых в какие-то степени: 3 в 4 степени и 2 в 3 степени. Действительно, 3 в 4 степени больше 2 в 3 степени, но 3 в 4 степени это 81, а не 27)
Спасибо большое за очень понятное объяснение всех тем!
Лиса, рады что понравилось. Описку в примере исправили)
1,7>14/8 (14/8 перевести в десятичную дробь) — кажется, здесь знак неверно стоит
Спасибо, Ольга. Действительно неправильно. Исправили