Подобие треугольников
Что такое равные треугольники, понятно более или менее всем: их можно правильно наложить – и они совпадут.
А вот что такое подобные треугольники? Вроде как «похожие», но как это понимать? И для чего это понимать?
Ну например для решения задание ЕГЭ №16, где подобие треугольников используется для доказательств. Кстати, полностью 16-ю задачу решают менее 1% выпускников!
Читай эту статью, смотри вебинар по 16 задаче и все поймешь!
Подобие треугольников — коротко о главном
Подобные треугольники – это треугольники, у которых все углы равны и все стороны строго пропорциональны.
Коэффициент пропорциональности называется коэффициентом подобия \( \displaystyle k\).
Если \( \displaystyle \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}\) с коэффициентом подобия \( \displaystyle k\), то:
\( \angle A = \angle {A_1},\angle B = \angle {B_1},\angle C = \angle {C_1}\)
Отношение периметров подобных треугольников равно коэффициенту подобия: \( \displaystyle \frac{{{P}_{ABC}}}{{{P}_{{{A}_{1}}{{B}_{1}}{{C}_{1}}}}}=k\).
Отношение площадей подобных треугольников равно квадрату коэффициента подобия: \( \displaystyle \frac{{{S}_{ABC}}}{{{S}_{{{A}_{1}}{{B}_{1}}{{C}_{1}}}}}={{k}^{2}}\).
Признаки подобия треугольников:
По двум углам:
\( \displaystyle \angle A=\angle {{A}_{1}}\), \( \displaystyle \angle C=\angle {{C}_{1}}\) \( \displaystyle \Rightarrow \)\( \displaystyle \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}\).
По одному углу и отношению заключающих его сторон:
\( \displaystyle \angle A=\angle {{A}_{1}}\), \( \displaystyle \frac{AB}{{{A}_{1}}{{B}_{1}}}=\frac{AC}{{{A}_{1}}{{C}_{1}}}\) \( \displaystyle \Rightarrow \)\( \displaystyle \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}\).
По отношению трех сторон:
\( \displaystyle \frac{AB}{{{A}_{1}}{{B}_{1}}}=\frac{AC}{{{A}_{1}}{{C}_{1}}}=\frac{BC}{{{B}_{1}}{{C}_{1}}}\) \( \displaystyle \Rightarrow \)\( \displaystyle \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}\).
Подобные треугольники — подробнее
Мы разобрали подробно все, что касается треугольников в общем. Кроме того мы рассмотрели отдельные темы:
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Теорема косинусов
- Теорема синусов
- Медиана
- Биссектриса
- Высота
Но что такое подобные треугольники?
Вот, например, такой и такой:
Похожи эти треугольники? Ты скажешь, конечно же нет!
А такой и такой?
Похожи!
А вот такой и такой?

Посмотри внимательно, тоже похожи.
А теперь строго математически!
Треугольники называются подобными, если у них все углы равны и все стороны пропорциональны.
То есть все углы равны и все стороны одного треугольника в \( \displaystyle 5\), или, в \( \displaystyle 7\), или в \( \displaystyle 8,21\) (или и т.д.) больше сторон другого треугольника.
Записываются слова «треугольник \( \displaystyle ABC\) подобен треугольнику \( \displaystyle {{A}_{1}}{{B}_{1}}{{C}_{1}}\)» с помощью такого значка:
\( \displaystyle {} \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}} \)
То число раз, в которое отличаются стороны подобных треугольников, называются коэффициентом подобия, обозначается обычно с помощью буквы \( \displaystyle k\).
То есть, если
\( \displaystyle \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}\) с коэффициентом подобия \( \displaystyle k\), то это означает что

\(\angle A = \angle {A_1},\angle B = \angle {B_1},\angle C = \angle {C_1}\)
и \( \displaystyle \frac{{AB}}{{{A_1}{B_1}}} = k,\frac{{AC}}{{{A_1}{C_1}}} = k,\frac{{BC}}{{{B_1}{C_1}}} = k\)
Можно было бы все так и оставить, но, как и в случае с равенством треугольников, ленивым математикам стало слишком неохота проверять равенство ВСЕХ трех углов, и пропорциональность ВСЕХ трех сторон.
И они придумали признаки подобия треугольников.
Признак подобия треугольников «по двум углам»
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Помнишь еще, что «\( \displaystyle \sim{\ }\)» обозначает слова «подобен»?
Осознай удобство! Вместо того, чтобы проверять 6 утверждений – 3 равных угла и 3 пропорциональных стороны – ДОСТАТОЧНО РАВЕНСТВА ВСЕГО ДВУХ УГЛОВ! И это вообще-то самых удобный и часто используемый признак.
Но есть и еще два. Смотри.
Признак подобия треугольников «две пропорциональные стороны и угол между ними»
Если треугольники имеют одинаковый угол, и стороны, заключающие этот угол, пропорциональны, то такие треугольники подобны.

Признак подобия треугольников «три пропорциональные стороны»
Если три стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

Самый главный «секрет» подобия треугольников
Признаки нам рассказали о том, как обнаружить подобные треугольники, а теперь, как же воспользоваться найденным?
Скажем, ты установил, что \( \displaystyle \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}\) с коэффициентом подобия \( \displaystyle 2\). Так, кстати, часто бывает, когда проводят среднюю линию…
Ну вот, что же хорошего? А то, что тогда…
Все элементы одного треугольника ровно в \( \displaystyle 2\) (или сколько у тебя выйдет раз) больше, чем элементы другого треугольника.
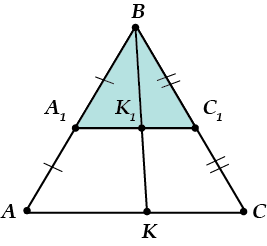
Не только стороны, но и высоты, биссектрисы, медианы, радиусы вписанной и описанной окружности и т.д.
Есть одно важное исключение: площадь.
Запомни:
Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 16. Подобие треугольников. Задачи на доказательство
Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!
Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников для расчетных задач (не только для доказательств).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Иван
15 ноября 2019
В 3 признаке подобия, как мне кажется, ошибка. Не три стороны должны быть пропорциональны, а всего лишь две.
Алексей Шевчук
15 ноября 2019
Иван, вы путаете с признаком «по двум углам»: если пропорциональны только 2 стороны, то третья может быть какой угодно. Например, треугольник со сторонами 3, 4, 5 — прямоугольный, а со сторонами 6, 8, 9 — остроугольный, они подобными быть не могут, хотя 2 стороны у них пропорциональны: 3:6=4:8. С тремя углами это работает, поскольку третий угол автоматически оказывается равным, благодаря тому, что сумма всех углов треугольника = 180.
Максим
14 декабря 2019
Все правильно , если по другому учат только.
Genius
07 мая 2020
Нет, там всё правильно