Треугольник — основные понятия, свойства и признаки
На тему «Треугольник», пожалуй, можно было бы написать целую книжку. Что мы и сделали.
Но книжку целиком читать слишком долго, правда?
Поэтому мы сначала рассмотрим только факты, которые касаются вообще любого треугольника.
А потом рассмотрим такие темы как равнобедренный треугольник, прямоугольный треугольник, теоремы косинусов и синусов.
Все это ты найдешь здесь. Но читай книжку по кусочкам, чтобы не «поперхнуться» 🙂
Треугольник — коротко о главном
Определение треугольника:
Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Основные понятия:
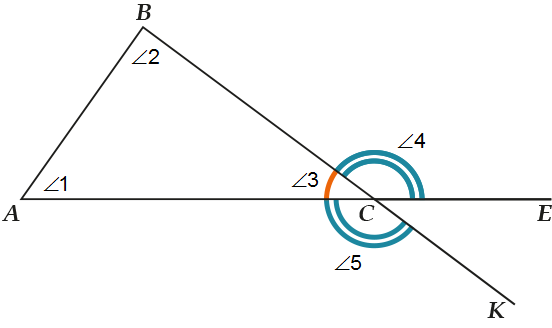
- \( \displaystyle \angle 1\), \( \displaystyle \angle 2\), \( \displaystyle \angle 3\) – внутренние углы \( \displaystyle \triangle ABC\)
- Внешний угол треугольника – угол, смежный внутреннему углу треугольника, т.е. \( \displaystyle \angle 4\) и \( \displaystyle \angle 5\) – внешние углы \( \displaystyle \triangle ABC\) при вершине \( \displaystyle C\).
Основные свойства:
Сумма внутренних углов любого треугольника равна \( \displaystyle 180{}^\circ \), т.е. \( \displaystyle \angle 1+\angle 2+\angle 3=180{}^\circ \)
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним, т.е. \( \displaystyle \angle 4=\angle 1+\angle 2\) или \( \displaystyle \angle 5=\angle 1+\angle 2\)
Сумма длин любых двух сторон треугольника больше длины его третьей стороны, т.е. \( \displaystyle \begin{array}{l}AB+BC>AC\\AB+AC>BC\\AC+BC>AB\end{array}\)
В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол, т.е.
если \( \displaystyle \angle 2>\angle 1\), то \( \displaystyle AC>BC\), и наоборот,
если \( \displaystyle AC>BC\), то \( \displaystyle \angle 2>\angle 1\).
Признаки равенства треугольников:
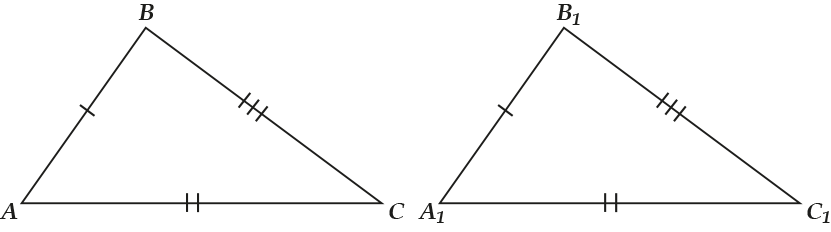
1. По двум сторонам и углу между ними

2. Второй признак – по двум углам и прилежащей стороне.

3. Третий признак – по трём сторонам.
Сумма углов треугольника. Внутренние и внешние углы
Внутренние углы треугольника
Сумма внутренних углов любого треугольника равна \( \displaystyle 180{}^\circ \).
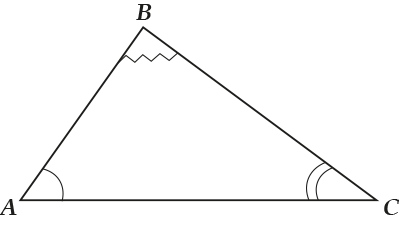
Единственное, что тебя может смущать в нашей формулировке – это слово «внутренних».
Зачем оно тут? А вот именно затем, чтобы подчеркнуть, что речь идёт об углах, которые внутри треугольника.
А что, разве бывают ещё какие-то углы снаружи? Вот представь себе, бывают.
У треугольника ещё бывают внешние углы.
И самое главное следствие из того факта, что сумма внутренних углов треугольника равна \( \displaystyle 180{}^\circ \), касается как раз внешнего треугольника.
Внешние углы треугольника
Так что давай выясним, что же такое этот внешний угол треугольника.
Смотри на картинку: берём треугольник и одну сторону (скажем \( \displaystyle AC\)) продолжаем.
Видишь, получился новый угол, \( \displaystyle \angle BCE\)?
Этот угол образован одной стороной (\( \displaystyle BC\)) треугольника и продолжением другой стороны (\( \displaystyle AC\)).
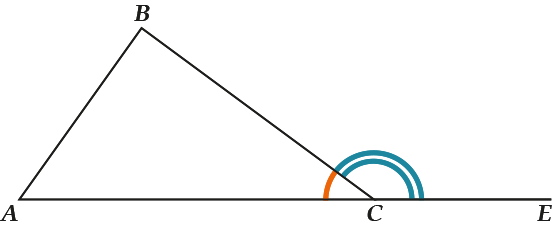
Вот он и называется внешним углом треугольника \( \displaystyle ABC\) при вершине \( \displaystyle C\).
Конечно, мы бы могли оставить сторону \( \displaystyle AC\), а продолжить сторону \( \displaystyle BC\). Вот так:
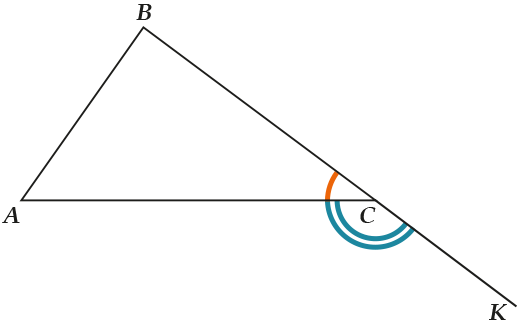
Тогда \( \displaystyle \angle ACK\) тоже будет внешним углом при вершине \( \displaystyle C\), да и к тому же он будет равен углу \( \displaystyle BCE\).
Смотри:
Углы \( \displaystyle BCE\) и \( \displaystyle ACK\) – равны как вертикальные, и оба они имеют право называться внешним углом при вершине \( \displaystyle C\).
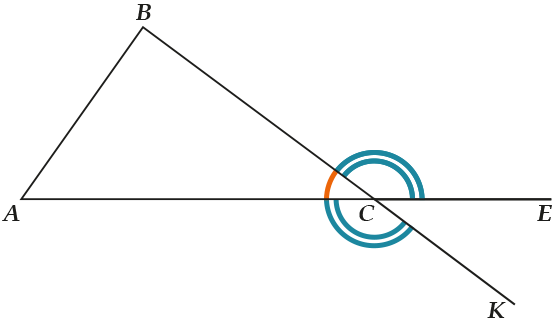
А вот про угол \( \displaystyle ECK\) такого сказать ни в коем случае нельзя!
Он образован пересечением двух продолжений сторон!
Угол \( \displaystyle ECK\) вообще равен внутреннему \( \displaystyle \angle C\) треугольника \( \displaystyle ABC\).

Так что не каждый угол снаружи треугольника имеет право называется внешним углом, а только тот, который образован одной стороной и продолжением другой стороны.
Так что же мы должны знать про внешний угол?
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
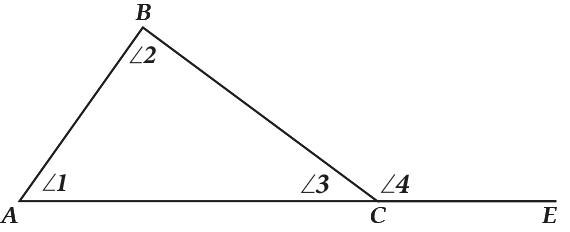
Смотри, на нашем рисунке это означает, что \( \angle 4=\angle 1+\angle 2\).
Как же это связано с суммой углов треугольника?
Давай разберёмся. Сумма внутренних углов равна \( \displaystyle 180{}^\circ \Rightarrow \)
\( \angle 1+\angle 2+\angle 3=180{}^\circ \),
но \( \angle 4+\angle 3=180{}^\circ \) – потому, что \( \angle 3\) и \( \angle 4\) – смежные.
Ну вот и получается: \( \angle 4=\angle 1+\angle 2\).
Видишь как просто?! Но очень важно. Так что запоминай:
Сумма внутренних углов треугольника равна \( 180{}^\circ \), а внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Неравенство треугольника
Следующий факт касается не углов, а сторон треугольника.
Сумма любых двух сторон треугольника больше его третьей стороны.
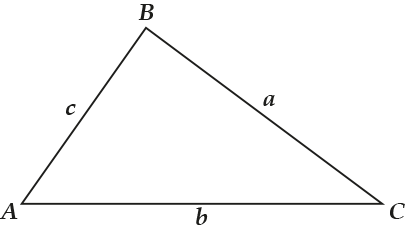
Это означает, что:
- \( a+b>c\)
- \( a+c>b\)
- \( b+c>a\)
Ты уже догадался, почему этот факт называется неравенством треугольника?
Ну вот, а где же это неравенство треугольника может оказаться полезным?
А представь, что у тебя есть три друга: Коля, Петя и Сергей.
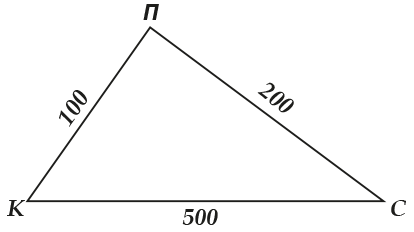
И вот, Коля говорит: «От моего дома до Петиного \( 100\) м по прямой». А Петя: «От моего дома до дома Сергея \( 200\) метров по прямой». А Сергей: «Вам хорошо, а от моего дома до Колиного аж \( 500\) м по прямой».
Ну, тут уже ты должен сказать: «Стоп, стоп! Кто – то из вас говорит неправду!»
Так не может быть!
Почему?
Да потому что если от Коли до Пети \( 100\) м, а от Пети до Сергея \( 200\) м, то от Коли до Сергея точно должно быть меньше \( 300\) (\( =100+200\)) метров – иначе и нарушается то самое неравенство треугольника.
Ну и здравый смысл точно, естественно, нарушается: ведь всякому с детства неизвестно, что путь до прямой (\( КС\)) должен быть короче, чем путь с заходом в точку \( П\). (\( К-П-С\)).
Так что неравенство треугольника просто отражает этот общеизвестный факт. Ну вот, ты теперь знаешь, как отвечать на такой, скажем, вопрос:
Бывает ли треугольник со сторонами \( 1,3,7\)?
Ты должен проверить, правда ли, что любые два числа из этих трёх в сумме больше третьего. Проверяем: \( 1+3<7\), значит, треугольника со сторонами \( 1,3\) и \( 7\) не бывает! А вот со сторонами \( 2,4,5\) – бывает, потому что
- \( 2+5>4\)
- \( 2+4>5\)
- \( 4+5>2\)
Равенство треугольников
Ну вот, а если не один, а два или больше треугольников. Как проверишь, равны ли они? Вообще-то по определению:
Два треугольника равны, если они совпадают при наложении.
Но…это ужасно неудобное определение! Как, скажите на милость, накладывать два треугольника хотя бы даже в тетради?!
Но на наше счастье есть признаки равенства треугольников, которые позволяют действовать умом, не подвергая риску тетрадки.
Да и к тому же, отбросив легкомысленные шуточки, открою тебе секрет: для математика слово «наложить треугольники» означает вовсе не вырезать их и наложить, а сказать много-много-много слов, которые будeт доказывать, что два треугольника совпадут при наложении.
Так что ни в коем случае нельзя в работе писать «я проверил – треугольники совпадают при наложении» – тебе это не засчитают, и будут правы, потому что никто не гарантирует, что ты при наложении не ошибся, скажем, на четверть миллиметра.
Итак, какие-то математики сказали кучу слов, мы за ними эти слова повторять не будем (разве что в последнем уровне теории), а будем активно пользоваться тремя признаками равенства треугольников.
Первый признак равенства треугольников
Если две стороны и угол между ними в одном треугольнике соответственно равны двум сторонам и углу между ними в другом треугольнике, то эти треугольники равны.

Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

В обиходе (математическом) приняты такие укороченные формулировки – их легче запомнить и применять:
- Первый признак – по двум сторонам и углу между ними;
- Второй признак – по двум углам и прилежащей стороне;
- Третий признак – по трём сторонам.
Типы треугольников (прямоугольный, равнобедренный, равносторонний) и другая теория по треугольникам
В этом разделе ты сможешь ознакомиться со всем, что касается треугольников и закрыть эту тему полностью!
Просто переходи по ссылкам:
Бонусы: Вебинары из нашего курса по подготовке к ЕГЭ по математике
В этом разделе вы найдете несколько вебинаров из нашего курса по подготовке к ЕГЭ по математике.
От самого простого (но важного!) на площадь фигур на клетчатой бумаге, до сложного 16 задания ЕГЭ на доказательство подобия треугольников (по которому максимальный балл получают менее 1% учеников!
Выбирайте вебинар по силам и учитесь решать задачи!
ЕГЭ 3. Площадь фигур на клетчатой бумаге
Клетчатая бумага очень удобная для геометрии. В основном тем, что на ней очень легко рисовать прямые углы.
А если прямой угол достроить к какому-то отрезку, то получится прямоугольный треугольник. А для прямоугольного треугольника можно записать теорему Пифагора — и вот уже мы определили длину нашего отрезка.
И хотя в 2021 году задача на геометрию на клечатой бумаге не будет входить в ЕГЭ, она очень полезна для того, чтобы начать изучать геометрию, для понимания планиметрии.
ЕГЭ 6. Прямоугольный треугольник: свойства, теорема Пифагора, тригонометрия
Подавляющее большинство задач в планиметрии решается через прямоугольные треугольники.
Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных. Но на уроках этой темы мы убедимся, что это действительно так.
Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше. И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными.
В этом видео мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.
ЕГЭ 6. Равнобедренный треугольник, произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ.
Очень часто все «проблемы» с решением задач на равнобедренный треугольник решаются построением высоты.
Также мы научимся решать и «обычные» треугольники. Убедимся в достоверности утверждении из прошлого урока о прямоугольных треугольниках https://youtu.be/ZKGTVfaiGe8) — очень часто решение задач сводится к нескольким прямоугольным треугольникам.
ЕГЭ 6, 14, 16. Теорема косинусов и синусов
Универсальный инструмент при решении треугольников — это теоремы косинусов и синусов. Они подходят для любых треугольников, а не только для прямых (как теорема Пифагора).
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
На этом уроке мы выучим сами теоремы и научимся применять их при решении задач первой части.
ЕГЭ 16. Подобие треугольников. Задачи на доказательство
Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!
Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников для расчетных задач (не только для доказательств).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org


